考慮客戶服務水平的原料采購、生產計劃最優化聯合決策模型

朱念劬， 盛 蓉（復旦大學 管理學院，上海 200433）

ZHU Nian-qu,SHENG Rong (School of Management,Fudan University,Shanghai 200433,China)

0 引 言

在競爭日趨激烈的市場中，現代企業愈發注重對自己運營成本以及客戶服務質量的控制問題。尤其是許多大中型生產企業，它們在一個生產階段內往往會接到不同買家的多個訂單，那么如何根據客戶的重要程度及訂單的數量，在最優化成本的前提下，來制定相應的原材料采購和生產計劃，是大家所比較關心的問題。本文針對上述問題，結合原材料生產商/供貨代理商的選擇，以及供貨、物流運輸過程中的多階段折扣，給出了相應的多目標規劃問題模型和相應的啟發式算法，并用一個比較簡單的例子進行了驗證。

供應商選擇以及采購配額、生產計劃決策問題是學術界和企業都十分關注的優化決策問題，許多研究者發表了相關的論文，提出了不少的研究方法，尤其是關于供應商選擇的方法有很多種，包括采購成本法、層次分析法 （AHP）、數據包絡分析（DEA）、模糊評價方法等。目前這方面研究主要集中在兩方面，其一是關于隨機需求的供應商選擇與采購量分配問題，Kasilingam R G、Alain Martel、關志民等分別針對隨機需求下的單階段、多階段以及單階段考慮價格折扣的問題進行了討論[1-3]，Sawik、Tadeusz集中研究了多產品生產計劃的隨機控制問題[4]，Elsevier Amsterdam提出了多產品隨機需求下的周期策略模型[5]，Bassok Y和Anupindi R則將Newsboy問題結合進來，對零配件的訂購決策進行考慮，他們所考慮的也是一個有限階段決策的問題[6]。另一方面的研究集中在確定性的需求下，如Pan A C、Jayaraman V、Narasimhan R等在原材料采購量分配方面提出了很多模型和方法[7-9]，這當中Pan A C、Jayaraman V都將供應商的選擇同供應量的分配建立在同一個模型當中進行考慮[7-8]，分別為混合整數規劃和線性規劃，Pan A C的線性規劃較簡單，考慮的因素少[7]；而Jayaraman V給出了一個單階段決策的綜合模型[8]。Narasimhan R主要研究了典型的供應量分配問題，建立了單階段下大型生產企業在固定的幾家供應商之間的采購量分配的數學模型[9]。段喆、朱道立在上述文獻的基礎上提出了一個多階段、多產品、考慮多級折扣水平的確定性需求的問題，給出了相應的供應量分配綜合模型并利用簡單的貪婪算法求解[10]。

縱觀上述關于采購分配問題的研究中，將采購和生產計劃聯合到一起進行考慮所受到的關注并不多，同時也很少有學者將顧客滿意度置入最優化問題當中，但不同客戶對于生產企業的重要性有輕重之分在現實當中是非常普遍的，因此研究這樣一個問題是有一定實際意義的。本文所研究的正是多階段、多產品、包括采購和運輸的多級折扣水平的確定性需求問題，同時考慮使得買家的顧客滿意度最大化，以及成本最優化的原材料采購和生產計劃制定的多目標規劃問題。

1 模型的構建

將問題總結為以下的一些描述和假設：

（1）企業將整個生產周期分為D個時間段，廠家的生產能力是有限的，一天最多生產A件產品。

（2）企業的原材料采購有兩個方向，一個是原材料生產廠家，一個是原料供應代理商。考慮到自身成本，原料生產廠家的發貨要求每個原料的單批訂貨量必須超過K1件，訂貨提前期為E1，同時提供多個折扣區段αi。而代理商可以提供小批量訂貨，但是最大供貨能力有限，假設每件產品的最大供貨量≤K2，訂貨提前期為E2，也提供一定的折扣段βi。上述兩類供貨商均使用總價折扣法。

（3）企業在這個生產周期內一共收到m張訂單，其中第k張訂單所訂購的產品i的數量為bki。每張訂單都有合同交貨日期，為Lk，總的生產周期長度為D，即要在時段D內完成所有訂單的生產任務，并盡量在合同交貨期之前將產品交付。

（4）廠家能夠生產n種產品，其中使用到t種原材料，每生產一件產品i所需的原材料j的數量為aij。每種產品的體積為Vi，每種原材料的體積為Vn+j，每件原材料j的重量為qj，原始單價為pj。

（5）企業的倉庫的倉儲能力是有限的，倉儲的內容包括原材料和未交付的產成品，不妨假設倉庫的最大容積為V。假設只有在一張訂單上的所有產品都生產出來以后廠家才會發貨，此時這張訂單的產品數量就不在庫存當中了。因此每d期的倉儲量=第d－1期的倉儲量+第d期收到的原材料量－第d期生產消耗的原材料量+第d期生產出的產品量－第d期完成訂單交貨量。

物流運輸費用分為兩部分，一類是固定費用FC，只要有運輸任務，就會產生該費用；一類是可變費用VC，它是由運輸貨物的重量決定的，采取分段折扣法，折扣因子為γt。

（6）決策者的目的首先是實現總成本的最優化，其次是提高顧客服務水平。從成本的角度來看，由于生產成本和產品的總量以及員工數有關，在這個問題當中我們假定訂單是已經給出的，并且所雇用的員工數也是無法改變的，因此這項費用比較固定，在模型的目標表達式中不考慮這筆費用，不會影響最優化的結果，因此我們主要考慮和原材料相關的采購、物流以及倉儲維護費用。從提高顧客服務水平的角度來說，本問題中只考慮各張訂單的實際交貨期相對合同交貨期提前的時長，根據各訂單所對應的買家的重要度不同，權重為σk，加權匯總得到的總顧客滿意度最大化。當然，在這個最優化的過程中，存在有些訂單不能在合同交貨期之前按時完成的可能性。

下面引入模型的決策變量：

設每期初倉庫中的原材料庫存量為rdj，因此生產周期開始時的原材料庫存為r1j；

因此有遞推式：

由生產產品消耗原材料的約束：

ydk——0-1變量，第k張訂單的交貨點：

滿足上述假設的基礎條件ydk≤yd-1,k。

對訂單k的每個產品i，因為已經有訂單必須完成的約束條件，因此只要給出能說明xdki和ydk的約束，及xdki≤Mydk?i，其中M是一個極大數。表明該訂單的生產期結束即不再生產屬于該訂單的任何產品，由生產周期內訂單數量必須完成的約束，那么就相當于給出了該訂單的所有產品都應在ydk=1的時段內完成。

倉儲總量的限制：

庫存約束為Wd≤V。

下面考慮成本，由于生產成本不予考慮，因此主要集中在與采購相關的采購成本、物流運輸成本和倉儲成本上。

（1）庫存成本

（2）采購成本

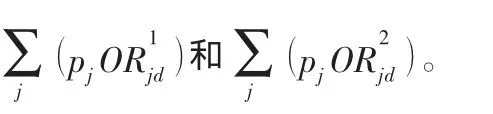
考慮生產商的折扣因子αu和對應的總價折扣區間構造一組0-1變量表征總價落在哪個折扣區間當中，滿足：

同樣考慮生產商的折扣因子βu和對應的總價折扣區間構造一組0-1變量表征總價落在哪個折扣區間當中，滿足：

因此總的物料采購費用為：

注意到此時折扣因子的存在使得費用關于決策變量呈非線性，因此在最優化計算中需要進行處理才能進行。

（3）物流運輸成本分為兩部分

①固定費用，即在當期一旦決定需要采購原料，則需要支付的固定費用。

需要引入一組對Cdt和edt的約束：

因而總成本為：

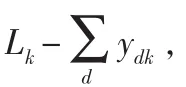
所以這個多目標規劃的目標函數為min｛ P1Z1-P2Z2｝。

2 模型求解

注意到上述模型中，在三個多級折扣的描述中，都出現了非線性的表達式，必須通過一定的方法轉變為線性約束后才能利用數學軟件求解。

構造三組約束：

在目標函數中，對成本和客戶服務水平進行權衡，給予上述兩個指標以相應的權重，就可以將上述多目標規劃問題轉換為混合整數線性規劃問題。上述介紹的模型在實際應用中應當屬于規模比較大的混合整數規劃，比如30時段的模型中決策變量要達到上千個，如果使用lingo進行求解，需要幾天時間甚至更多，另外約束條件的輸入也相當復雜，操作性比較差。因此本文嘗試了啟發式算法進行求解。啟發式算法分為兩個階段，第一階段先找出上述問題的一個可行解，第二階段通過逐步優化改進上述可行解得到一個近似最優解。具體操作步驟如下：

第一階段：尋找可行解。

（1）將所有訂單按照顧客服務水平的權重進行排序；

（2）根據企業的最大生產能力約束，按照上述排序依次制定各訂單產品的生產計劃；

（3）因為只有在某張訂單上所有的產品都生產出來以后才能交貨，因此根據上述生產計劃判斷庫存的產品是否會造成庫存溢出，并相應地對生產計劃進行調整；

（4）根據上述生產計劃，計算各期d所需的原材料數量，判斷從哪個貨源進貨，根據貨源的訂貨提前期制定采購計劃；

（5）計算上述過程中的采購費用、物流費用和庫存費用。從而得到了一組可行解，顯然它不是最優的，因此進入下一步驟。

第二階段：優化改進。

（6）從最后一期開始，計算各期庫存中的剩余空間，推算如果將下一期生產需要的原料盡可能地提前到這期采購能否提高折扣等級，相應降低的采購成本與因此增加的庫存成本哪個更大，決定是否將采購批次合并，轉向 （7）；

（7）計算當前解的客戶服務水平指標 （可能有些訂單會在合同交貨期后才能完成，這種情況在現實中的確存在），嘗試是否存在交換兩個訂單的順序，根據第一階段中的方法相應地改變生產計劃，使得最終顧客服務水平提高。如果存在，根據 （7）中新的生產計劃利用 （4）、（6）兩步得到相對的采購計劃，再根據 （5）計算總成本是否得到改進，轉向 （8）；

（8）計算各期企業的生產能力剩余，嘗試是否存在將一些訂單的產品生產提前，能夠提高客戶服務水平指標。如果存在，則改變生產計劃，并相應地調整采購計劃和庫存量估計，然后轉向 （6）；

（9）若經過上述3步都沒有發生改變，那么可以認為得到了問題的一個穩定解。

可以看到，上述啟發式算法能夠在較短的時間內得到問題的一個比較滿意的解，解的優化程度和運算的時間部分相關，運行時間越長，得到解的效果就越好。

對于小規模的此類模型，可以使用lingo求解或編程使用遞歸的搜索方法，下面就給出一個小規模模型的例子。

3 實例分析

考慮一個比較簡單的2產品2原料3訂單的例子，生產周期D=5，只考慮向原料生產商訂貨，訂貨提前期為1單位時間。這組數據的規模比較小，可以優化得到最優解。

表1 產品生產的原材料構成

表2 訂單具體信息

企業的生產能力為每天5000件產品，單位庫存費用為0.15。運輸每次固定費用為2000，單位重量費用為0.3。單次采購費用超過25000后享受9折的優惠。經過權衡以后，客戶服務水平在目標函數中的系數為10000，成本的系數為1。將上述參數代入模型輸入到lingo中進行求解。

得到模型的最優解

表3 產品、原材料系數

表4 Lingo求解最優生產計劃

因此在最優決策下，總成本為90550，客戶服務水平指標為3.7。

下面試著用上述啟發式解法來求解這個例子。

首先找出可行解 （有初始原材料庫存約束）：訂單的排序為1、2、3。

表5 Lingo求解最優采購計劃

表6 啟發式算法找出可行解

客戶服務水平為指標0.8，總成本為108998.6，其中采購、物流、倉儲成本分別為67500，23600，17898.6。

根據 （7），發現交換訂單2和訂單1的生產順序之后，可以實現服務水平的提高。由此改進了解。

客戶服務水平指標為3.7，總成本為91100，其中采購、物流、倉儲成本分別為65000，21600，4500。

轉向 （6），發現將三次采購合并為兩次，并適當提高第一次采購的量，能夠使得第一次采購享受到折扣，并且降低物流成本，因此調整當前解。

表7 啟發式算法改進可行解

表8 進一步調整當前可行解

客戶服務水平指標為3.7，總成本為90550，其中采購、物流、倉儲成本分別為63000，19600，7950。

再循環一次第二階段步驟沒有發生改變，因為認為得到了一組滿意解，和用Lingo計算得到的最優解是完全一致的。因此認為在問題規模比較小的條件下，使用啟發式解法也可以通過有限次循環得到問題比較滿意的近似最優解。

4 結 論

本文提出了一種兼顧生產型企業的生產采購成本和客戶服務水平，可以在多原材料供應商、代理商以及多級采購、物流折扣條件下的原料采購、生產計劃聯合最優化決策模型，給出了相應的啟發式算法，并通過一個簡單的例子檢驗了它的實用性。尤其是目前眾多大中型企業都特別關注采購成本，本文提出了共同制定采購與生產計劃，并且比較創新地將客戶服務水平融入模型中，具有一定的實際意義。

在企業的運營中，大規模的最優化問題占絕大多數，小規模的模型一般很難解決實際中遇到的問題。本文在實現運營成本最優和顧客滿意度最大化的建模中，使用了比較多的決策變量，從理論上來看是比較完善的，但是在實際計算中顯得較為復雜，本文提出的啟發式算法是否總是能夠得到較好的近似解仍然是一個疑問，可能隨著初始可行解獲取的不同而產生波動。當然，也可以通過在模型中減少時段數量等方法來降低計算復雜度，用小規模的模型去解原本大規模的問題，各時段內的生產安排可以由具體操作者靈活掌控，這也不失為一種辦法。同時，本文的所有討論都是基于確定性需求的前提下，而在考慮隨機產生訂單的時候，模型就會顯得十分復雜，目前未能提出很好的解決辦法。另外，在多級折扣因子的表達式中，如何優化模型的約束，將其轉換為線性規劃模型，也是值得關注的方向。

[1]Kasilingam R G,Lee C P.Selection of vendors-a mixed-integer programming approach[J].Computers&Industrial Engineering,1996,31(10)：347-350.

[2]Alain Martel,Moustapha Diaby,Fayez Boctor.Multiple items procurement under stochastic nonstationary demands[J].European Journal of Operational Research,1995,87：74-92.

[3]關志民，周寶剛，馬欽海.多產品采購條件下的供應商選擇與訂購量分配問題研究[J].計算機集成制造系統，2005,11(11)：1626-1632.

[4]Sawik,Tadeusz.Stochastic optimal control of a multi-facility,multi-product production scheduling with random times of supplies[J].Control Cybernet,1977,6(3-4)：21-35.

[5]Elsevier Amsterdam.Multi-product stochastic-demand periodic-review inventory and production cycling policies[J].Inventory in Theory and Practice,1986,3：489-503.

[6]Bassok Y,Anupindi R.Analysis of supply contracts with total minimum commitment[J].IIETransactions,1997,29：373-381.

[7]Pan A C.Allocation of order quantity among suppliers[J].Journal of Purchasing and Materials Management,1989(3)：36-39.

[8]Jayaraman V,Srivastava R,Benton W C.Supplier selection and order quantity allocation：a comprehensive model[J].The Journal of Supply Chain Management,1999(1)：50-58.

[9]Narasimhan R,Stoynoff L K.Optimizing aggregate procurement allocation decisions[J].Journal of Purchasing and Materials Management,1986(1)：23-30.

[10]段喆，朱道立.多階段多產品供應量分配的綜合模型[J].系統工程，2004,22(6)：21-24.