證券市場套利模型及應用研究

○陳溟

（內蒙古科技大學數理與生物學院 內蒙古 包頭 014010）

證券市場套利模型及應用研究

○陳溟

（內蒙古科技大學數理與生物學院 內蒙古 包頭 014010）

本文研究了在證券市場中單因素影響下的套利模型和雙因素影響下的套利模型，并在證券市場中就套利模型的應用進行了分析，為投資者進行決策提供了有效的分析方法。

套利模型 單因素模型 雙因素模型

與投機相比，套利具有其獨特的優勢，因此有必要對套利模型進行深入探討。從長期來看，證券收益率存在較多的影響因素，這些影響因素和證券收益率之間又存在紛繁復雜的關系；從中短期來看，證券收益率的影響因素相對較少，并且比較容易辨別其影響程度的強弱。因此，為了便于對套利模型進行研究，及時捕捉套利機會，本文僅研究周期為兩周的短期套利模型。

一、單因素的套利模型

假設證券i的期望收益率與某一因素存在一定的相關關系。設該影響因素為F，則得到模型：

其中，ri為預期收益率，βi為影響因素F的敏感系數。設其他的影響因素極其微弱，即εi=0，則有方程：

公式（2）中，當F=0時，則得ri=αi=rf，也就是無風險收益率，它是一個固定的常數。只要能夠準確地估計出每支股票對影響因素F的敏感程度βi，若F的值是可以量化的，就可以根據公式（2）算出預期收益率ri；若因素F是定性的，則可以根據敏感程度，由主觀判斷來估計預期收益率ri。

如果存在這樣一種股票組合，投資者無需追加資金，組合風險為0，收益率大于0，則形成可套利的股票組合，這時就為套利行為打開了方便之門。設Δxi為持有第i種股票的改變量，若投資者只持有三支股票，則套利股票組合必須同時滿足以下三個條件（假設不考慮套利的交易費）：

根據公式（3）中的前兩個條件，可以得出無窮多組解。因此可以任取Δx1=m，則由公式（3）前兩個條件有：

由公式（4）可得：

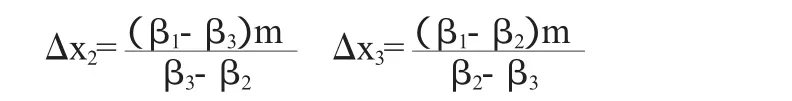
將Δx1，Δx2，Δx3的值代入公式（3）中的第3個方程得：

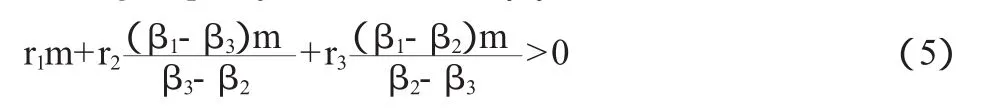
若（5）式成立，則反映出三種股票的組合沒能達到均衡，也就意味著存在套利機會。

投資者只要對變動量為負的股票做空頭，而對變動量為正的股票做多頭，這樣可以再無需追加資金又不冒任何風險（若非因素風險很小）的情況下獲利。

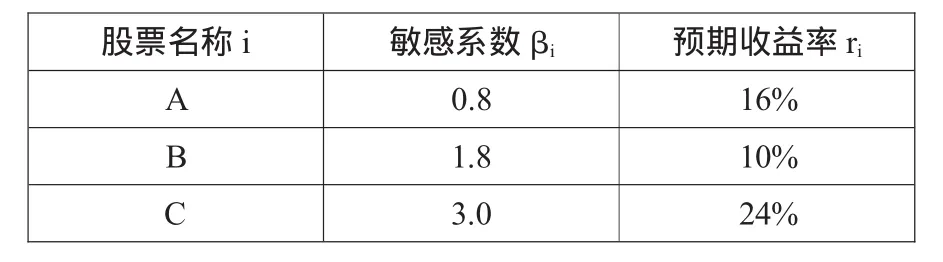
表1 三支股票的相關資料

假設三種股票的預期收益率和影響因素F的敏感系數如表1所示，那么投資者三支股票的組合是否存在套利機會呢？三支股票的預期收益率與因素敏感度構成的散點圖中，出現的三點明顯不在同一條直線上，也就是說，根據散點圖，可以大致估計出股票組合沒有達到均衡狀態，因此可以判定存在套利機會。若不考慮套利行為產生的交易費用，則可以根據表1資料得出：

我們就這樣在鄉里唯一的，也是最繁華的“長安”大街上走著，在目光織成的網中穿過，似乎還聽見了竊笑聲。我想溜，又沒借口，想跑又跑不起來，只好低下頭，感到芒刺在背，苦不堪言。我斜眼見她挺著豐滿、高聳的胸脯瀟灑自若地走著，想和我說什么；我佯裝看腳下的路，只看見她一閃一閃，穿著白皮涼鞋的腳尖。

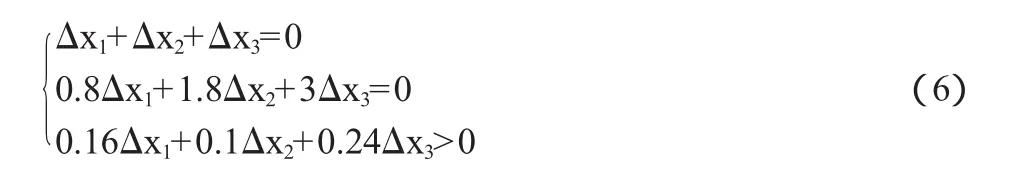
再設Δx1=6，由方程組

解得：Δx2=-11；Δx3=5。

將Δx1=6，Δx2=-11，Δx3=5代入公式（6）中的第3個式子得：

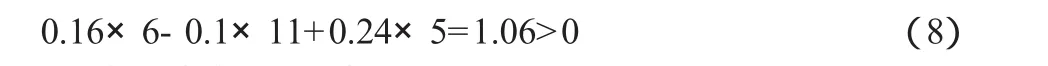
（8）式是成立的，見表2：

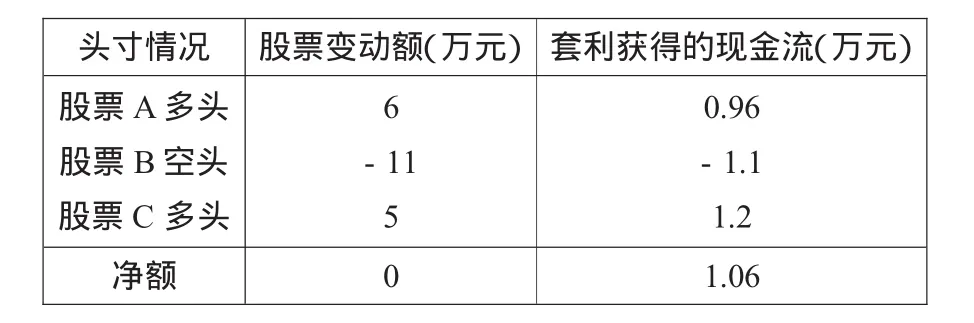
表2 投資者的套利結果

由表2可知，投資者通過減持股票B而獲取的11萬元資金用于購買6萬元的股票A和5萬元的股票C，股票變動量的凈額為0，而投資者的股票總市值仍然保持60萬元，既不增加投資，又不承擔風險，只要預期收益率能夠實現，就可以套取1.06萬元的現金收益。這也反映了股票A與股票C被市場低估，而股票B被高估，股票組合未能達到均衡狀態。隨著套利行為的不斷繼續，股票B因供過于求而遭到大量的拋售，從而導致股價下降，預期收益率逐漸上升；股票A和股票C因供不應求，致使大量資金涌入，股價紛紛抬升，預期收益率逐漸下降，此時宣布套利行為結束。

上面的三支股票的改變量是任意設定的?，F在來分析一般情況：設Δx1=m，代入公式（6）的前兩個式中得：

解得：Δx2=-1.83m，Δx3=0.83m?，F將Δx1=m，Δx2=-1.83m，Δx3=0.83m代入公式（6）的第3式中得：

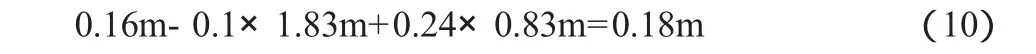
在現實中，套利行為也存在交易費，在證券市場上買賣股票，都必須要交納交易手續費（交易金額的0.3%）和印花稅（交易金額的0.2%）。因此（3）式就變成：

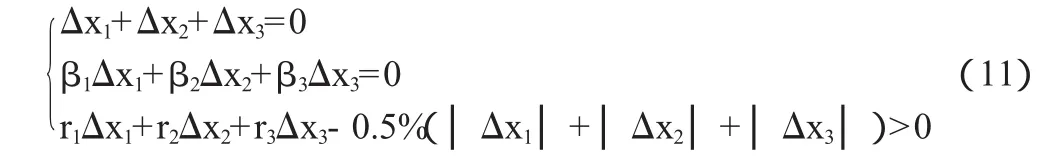
（11）式中，0.5%為交易手續費和印花稅系數，它是按交易金額來計算的。同理，設Δx1=m，代入公式（11）中的前兩個方程求得：

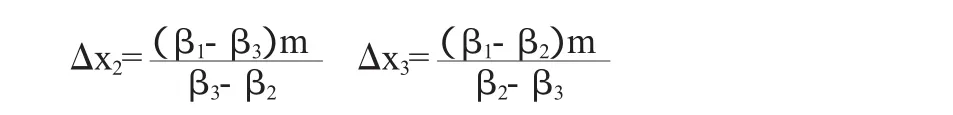
將Δx1，Δx2，Δx3的值代入公式（11）中的第3個方程中得：

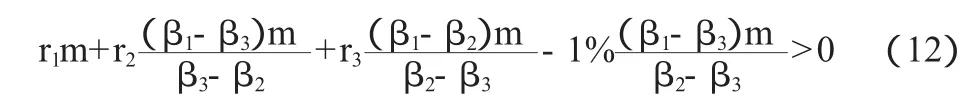
只要（12）式成立，就有套利機會。設交易手續費和印花稅為0.5%，（6）式就變成：

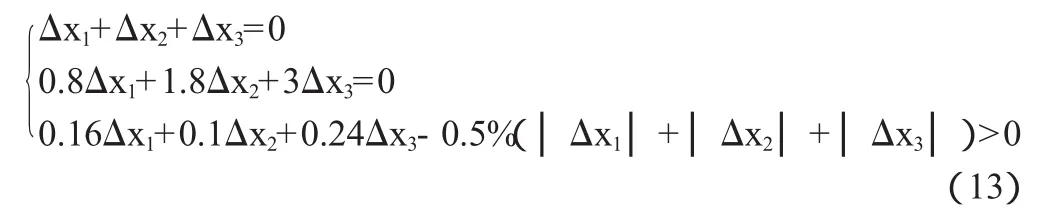
設Δx1=m，由（13）式可以解得Δx2=-1.83m，Δx3=0.83m，將3個改變量代入（13）式中第3個方程可得：

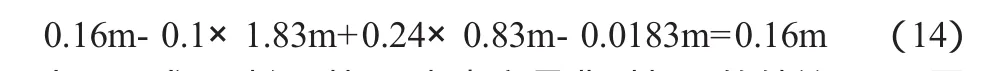
由（14）式可以得到與不考慮交易費時相同的結論，即只要改變量m為正數，就存在套利機會，并且隨著改變量m的增大，套利收益也逐漸增大。在理論中，改變量m不受限制，使套利收益可以趨于無窮大，但在現實的證券市場中，改變量m是受限制的，同樣為1.83m≤20，解得m≤10.91萬元。也就是說，股票A的最大改變量只能達到10.91萬元，在考慮交易費時，最大的套利收益為1.75萬元。

因此，投資者為了獲取最大的套利收益，可以通過賣空預期收益率低的股票，而購進預期收益率高的股票，一旦實現預期的收益率，便可以獲得套利收益。

二、雙因素模型

假設在短期內存在兩個影響較大的因素，分別設為F1，F2，其他的因素影響極其微弱，則得到模型：

其中，β1i，β2i分別為影響因素F1，F2的敏感系數。αi是無風險收益率。若影響因素F1，F2的值是可以量化的，就可以根據公式（15）算出預期收益率ri；若因素F1，F2是定性的，則根據敏感程度，由主觀判斷來估計預期收益率ri。

在證券市場中，套利通常需要考慮交易費。因此，在有交易費時，雙因素影響下的套利條件為：

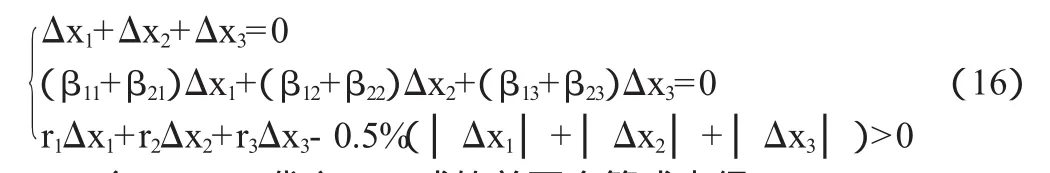
令Δx1=m，代入（16）式的前兩個等式中得：

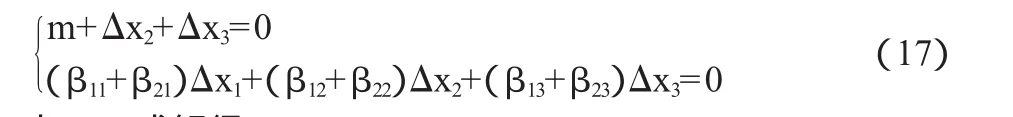
由（17）式解得：

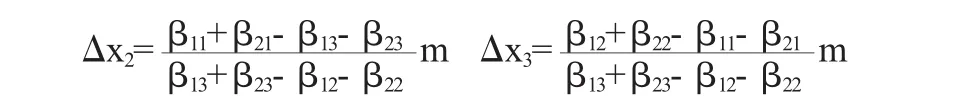
將Δx1，Δx2，Δx3的值代入（16）式中的第3式中，得出：

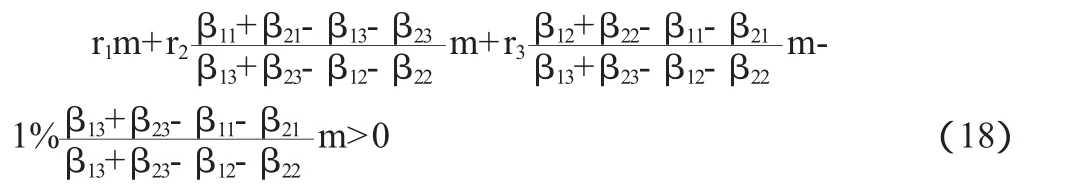
只要上面的不等式成立，就存在套利機會。

由于在短期內對股票的影響因素相對較少，因此在進行套利分析時，通常采用單因素模型和雙因素模型。而對于影響因素可能多于兩種的情況，則可以采取篩選的方法，選擇影響最大的兩個因素，利用雙因素模型來進行研究。投資者持有的股票組合可能多于三支，投資者只需將所有股票分成若干種三支股票的組合，利用單因素模型和雙因素模型進行分析后，尋找最佳的套利組合來進行套利。

三、結論

總之，套利相對于投機者來說是一種相對新型的謀利方式，這種方式不僅風險相對較?。ㄓ袝r甚至無風險），而且還可以謀取利潤。相對于風險較大的市場，套利技術的應用無疑是投資者最有利的選擇。但要真正掌握好套利技術，不僅對影響因素要有準確的估計，還要敏銳地把握住時機，這一切尤其需要大量的實戰經驗作為堅實的后盾。

應該說，套利定價模型僅僅是一個模型而已，它對實踐的擬合程度再高，模型設定得再合理，也只是一個近似的概念，不可能做到百分百的復制。實踐中，我們不能期望應用某個神奇的模型而獲利豐厚。“套利”為“投機”設置了極限，國外專業投資基金幾十年、上百年的業績分析報告也證明了這一點。理論要為實踐服務，理論是實踐的指導，理論本身就是寶貴的精神財富，理解、認識套利定價模型不僅可以填補在認識領域中的空白，也讓我們在實踐中更主動、更沉穩。

[1]哈姆·勒威、馬歇爾·薩納特著，陳云賢、朱敢林譯：證券投資組合與選擇[M].中山大學出版社，1995.

[2]黃良文：投資估價原理[M].北京科學出版社，2002.

[3]葉永剛：金融工程概論[M].武漢大學出版社，2000.

[4]王濤明：證券投資風險計量、預測與控制[M].上海財經大學出版社，2003.

（責任編輯：李文斐）

book=7,ebook=155