Cu3N 彈性和熱力學性質的第一性原理研究*

李世娜劉永

(燕山大學理學院，秦皇島066004)

(2010年1月11日收到;2010年1月30日收到修改稿)

Cu3N 彈性和熱力學性質的第一性原理研究*

李世娜?劉永

(燕山大學理學院，秦皇島066004)

(2010年1月11日收到;2010年1月30日收到修改稿)

利用基于密度泛函理論的第一性原理全勢線性綴加平面波方法，研究了立方反ReO3結構Cu3N在零溫(0K)零壓下的平衡晶格常數、體彈模量及其對壓強的一階導數，計算結果與其他實驗及理論結果基本相符.同時得出Cu3N的彈性常數，Poisson比等，并分析出Cu3N在零溫零壓下是穩定的.通過準諧Debye模型計算Cu3N的熱力學性質，得到了Cu3N的晶格常數、等壓比熱容、等容比熱容、熱脹系數與溫度和壓強之間的關系，同時計算出不同溫度不同壓強下其體彈模量及Debye溫度的值.

熱力學性質，彈性常數，第一性原理，Cu3N

PACC:0570C，6220D，7115A

1. 引言

過渡金屬氮化物由于在磁學、光學和形態學等方面的極好性質及在電子器件等領域的應用引起了人們的廣泛興趣，如化合物BN，AlN等，但共價氮化銅(Cu3N)為人們所不熟悉.Cu3N是一種以共價鍵結合的金屬氮化物.塊體的Cu3N晶體密度為5.84 g/cm3，分子量為204.63，顏色呈黑綠色或紅褐色.無毒廉價材料Cu3N具有較高的電阻率，較低的熱分解溫度和獨特的光電特性在光存儲器件和高速集成電路應用方面備受關注［1，2］.此外，Cu3N還是應用于低磁阻隧道結的阻擋層的候選材料［3］.

在3d過渡金屬(Ti，Cr，Fe，Co，Ni，Cu)的氮化物中，隨著原子序數的增大，與N2氣反應活性依次降低，Cu的反應活性最低.起初Cu3N只能通過Cu2O和NH3作為初始材料通過復分解反應制備得到［4］.近年來人們使用多種制備技術獲得Cu3N薄膜，如直流反應濺射法［5］、射頻磁控濺射發［6］、分子束外延法［7］、脈沖激光反應沉淀法［8］等.Cu3N薄膜的生長條件對它的結構性質等有一定的影響.國際上報道的有關Cu3N的物理及化學性質并不一致: Cu3N有時候表現出低反射率高阻抗的半導體性質，有時候表現出金屬性質［8，9］;Maruyama和Marushita指出Cu3N薄膜晶格常數a>3.868(1=10－10m)為導體，小于3.868為絕緣體［3］;熱分解溫度在100—400℃之間［7，10，11］等.因此對Cu3N開展研究非常有必要.

Cu3N是立方反ReO3結構，空間點群是Pm-3m，一個晶胞中Cu原子占據各立方邊邊線的中心位置而N原子占據立方晶胞的8個頂點，此結構的體心位置有一較大間隙，Cu原子以及其他原子如Pd、堿金屬原子等很有可能進入此位置導致Cu3N的電學性能、光學性能等發生很大的變化［2，12］.Yu等［13，14］得出Cu3N的帶隙隨壓強的增大而減小.在高壓下反ReO3結構的Cu3N由半導體向金屬相轉變.這使得該材料具有很大的潛在應用價值.但是運用全勢線性綴加平面波法計算彈性常數，以及結合Debye模型計算Cu3N的熱力學性質還沒有具體的報道.

本文利用全勢線性綴加平面波方法研究了塊狀反ReO3結構Cu3N的基本性質參數，獲得了Cu3N的平衡晶格常數a，體彈模量及其對壓強的一階導數、彈性常數.另外，通過準諧Debye模型計算了Cu3N在壓強0—5 GPa，溫度0—700K范圍內的Debye溫度、熱容量、熱脹系數α等熱力學性質.

2. 模擬方法

本文采用基于第一性原理的密度泛函理論［15］全勢線性綴加平面波法［16］進行計算，使用廣義梯度近似處理交換相關勢能(WIEN2K軟件包［17］).對Kohn-Sham方程和能量泛函進行了自洽求解，可以得到所求電子體系的基態密度、總能和能量本征值.在綴加平面波方法中，空間被分割為間隙區(intertitial region，簡記為IR)和以原子位置為中心的非重疊糕模球(muffin-tin，簡記為MT).每個MT球內波函數球諧基矢的角動量截斷取為lmax=10.波函數的平面波截斷由RMT*Kmax=8決定，其中RMT是晶胞中最小的MT半徑，Kmax是平面波展開中最大的倒格子矢量.在電荷密度Fourier展開中Gmax=14.Cu和N的MT半徑分別取為1.8 a.u.，1.6 a.u..自洽循環計算的收斂標準為0.0001電荷電量.

為了研究Cu3N的熱力學性質，使用了準諧Debye模型［18，19］.在此模型中，Cu3N的非平衡Gibbs函數G*(V;P，T)形式如下:

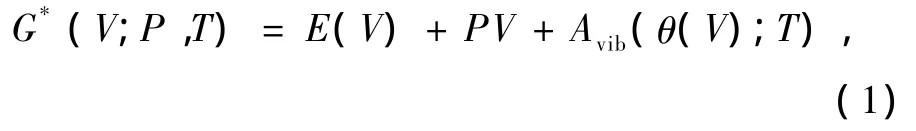
在(1)式的右邊，E(V)表示每個原胞的總能量，P，V和T分別表示壓強、體積和溫度，Avib是振動的Helmholtz自由能，其中Θ(V)是Debye溫度.考慮到準諧近似并使用聲子態密度的Debye模型，Avib可表示為［20，21］

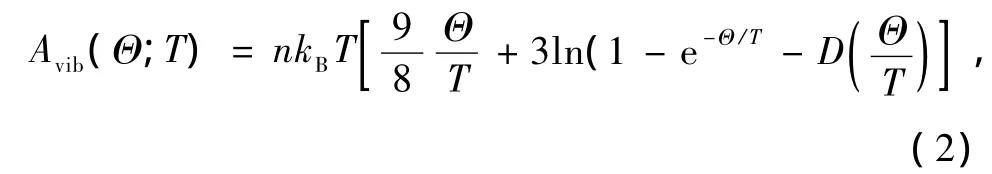
D(Θ/T)是Debye積分，n是每個原胞中包含的原子數，kB是Boltzmann常數.對于各項同性的固體來說，Θ可表達為［21］

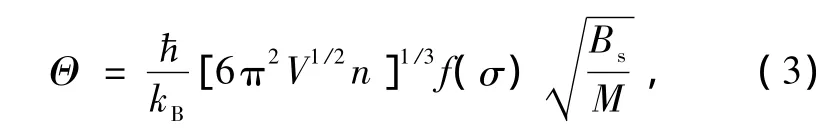
M是每個原胞中分子的質量，Bs是用來表示晶體壓縮率的絕熱體積模量，σ是Poisson比，可以表達為［20］

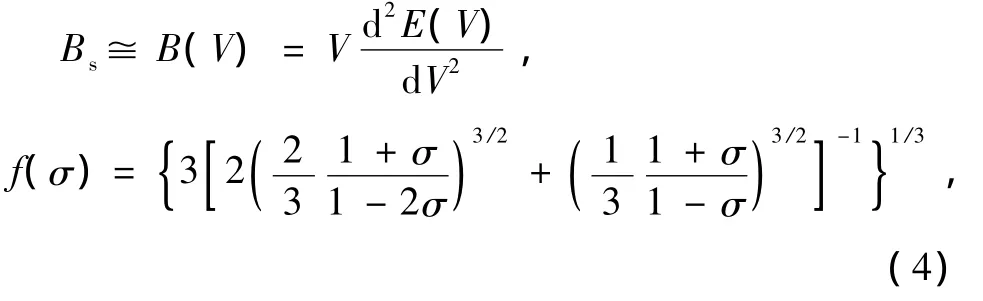
非平衡Gibbs函數G*(V;P，T)對體積求最小值，即

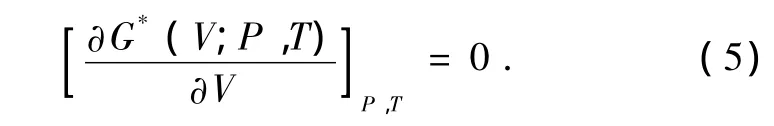
通過(5)式可以得到熱狀態方程(EOS)，

其中振動內能Uvib和Grüneisen參數γ表達式分別為［21］

等溫體彈模量BT，等容熱容CV，等壓熱容CP和熱膨脹系數α分別表示為［18］

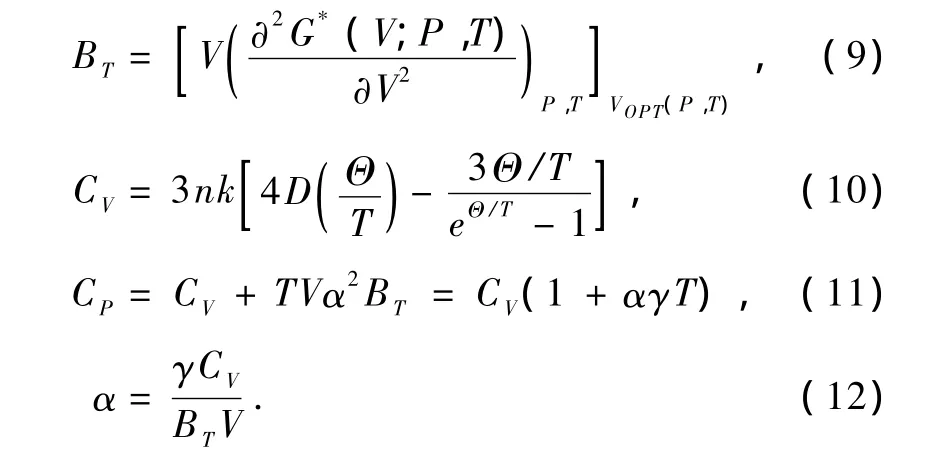
3. 結果與討論

3.1. Cu3N基本的性質參數

為了確定立方反ReO3結構Cu3N的體結構性質，我們采用Murnaghan狀態方程進行擬合［22］，計算了晶體體積與系統總能之間的關系.圖1為本文研究的Cu3N的結構圖，淺色小球表示N原子，黑色大球表示Cu原子.圖2為總能量E和原胞體積V的關系，本文計算出的能量為圖中縱軸所示能量減去136596 eV.由圖2知，Cu3N在零溫零壓下，V=56.32013是最穩定.由此，可求出零溫零壓下的晶格常數a0=3.833，體彈模量B0及其對壓強的一階導數B′0，如表1所示.所得結果與其他理論計算結果和實驗結果相符合.

圖1 Cu3N結構圖

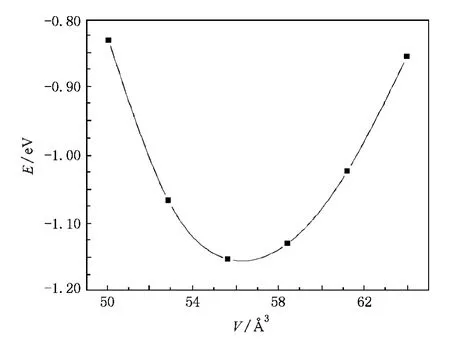
圖2 能量與體積關系圖

表1 在零溫零壓下Cu3N的晶格常數、體積模量及其對壓強的一階導數

3.2. 彈性常數

彈性性質跟晶體的比熱容、Debye溫度和熱容等性質密切相關.在研究立方反ReO3結構的Cu3N的彈性常數時，能獲得其結構穩定性等方面的信息.立方晶格Cu3N體系中包含3個獨立的彈性系數C11，C12和C44.如圖3彈性常數Cij通過以下3種變形方式得到:1)與結構優化相似的均勻體積膨脹和收縮的變形(EOS，如圖3(a)所示);2)沿［111］體對角線的菱方(rhomb)變形如圖3(b)所示;3)保持體積恒定沿［001］方向的四方(tetra)變形如圖3(c)所示.其中本文計算出的能量為圖中縱軸所示能量減去136596 eV.彈性常數通過體積模數B，剪切模量G，楊氏模量E和Poisson比σ來決定晶體對外力的響應［24］.

立方晶格的體彈模量與彈性常數Cij之間的關系為［25］:B=1/3(C11+C12).根據Voigt近似，剪切模量GV跟晶體彈性常數Cij有如下關系:GV=(C11－C12+3C44)/5.然而根據Reuss近似，又可得剪切模量GR跟晶體彈性常數Cij之間有如下關系:GR=5 (C11﹣C12)C44/［4C44+3(C11－C12)］.Hill證明，Voigt和Reuss的方程描述的分別是晶體剪切模量的上限和下限，給出晶體的剪切模量:G=1/2(GV+ GR).楊氏模量E，剪切模量G及體彈模量B之間的關系式為:E=9GB/(3B+G).

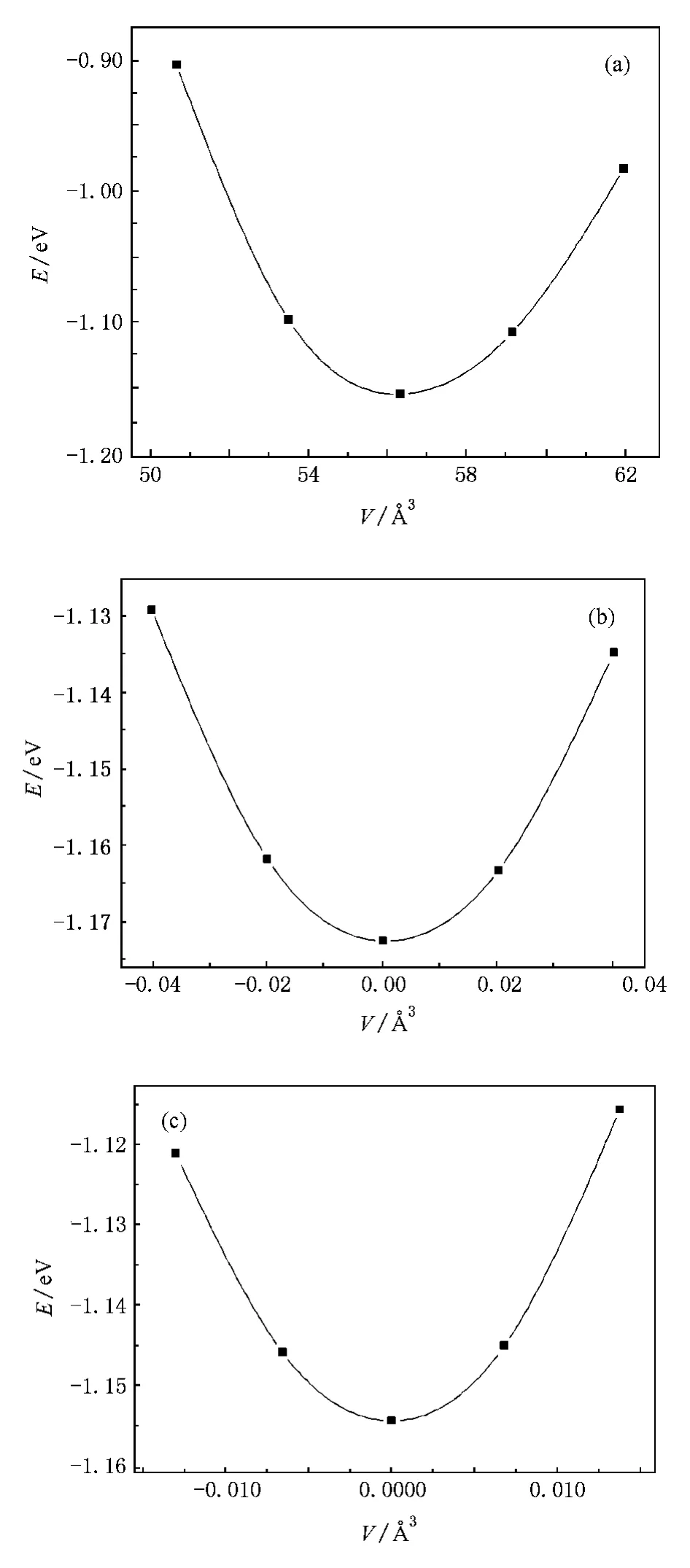
圖3 Cu3N三種彈性應變曲線(a)體積膨脹與壓縮的變形，(b)菱方變形，(c)四方變形

計算出的Cu3N的彈性常數Cij，剪切模量G等參數如表2所示.本文得到的Poisson比為σ=(3B－E)/6B=0.358102.由表2，Cu3N滿足以下條件［24］:

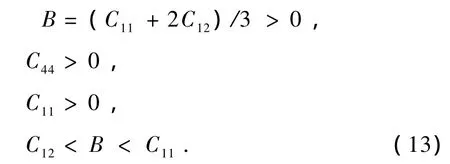
立方反ReO3結構的Cu3N在零溫零壓平衡條件下是穩定的.

表2 Cu3N的彈性常數a及各彈性模數值(單位:GPa)

3.3. 熱力學性質

本文有效地利用準諧Debye模型，計算了T在0—700K，P在0—5 GPa范圍內立方反ReO3結構的Cu3N的熱力學性質.

Cu3N的晶格常數a隨T和P的變化如圖4所示.在給定P下a隨T升高而增大，而在給定T下隨P的增大而減小.這是因為對材料增加P與降低T，所起到的效應幾乎是等同的.

從圖5中得到了零壓下Cu3N的體彈模量跟T的關系.當T<50K時，B幾乎保持不變，當T> 50K時，隨著T的增加，B急劇減小.由上，零壓下T <50K時，a幾乎保持不變，而T>50K，a隨T的升高而急劇增大，導致了Cu3N的體彈模量隨T升高而急劇減小.表3給出體彈模量BT及Debye溫度Θ與T和壓強的關系.兩者都是隨T的升高而減小，隨P的增大而增大.通過Debye模型得出的零溫零壓下的體彈模量與用第一性原理(見表1)得出的結果相比誤差為1.08%，兩者結果基本相符.本文計算出在T=300K零壓下，Cu3N的Debye溫度Θ=327.62 K.

圖6為Cu3N的熱容量在給定壓強下隨T的變化曲線.Cp與CV的關系如(11)式.Cp與CV隨T的升高而增大，隨壓強的增大而減小.CV在低溫時變化較快，與T3成比例，是因為Debye模型的準諧近似.在高溫時，準諧效應受限，受非諧效應的影響，CV趨向于Dulong-Pettit極限(對于單原子固體，CV～3NAKB)，即Cu3N的CV趨向于99.77 J·mol－1· K－1.這符合固體的共同性質.Cp在低溫時較快變大，而在高溫時并不趨于固定值.

圖4 Cu3N的a與T，P的關系(a)a分別在0，1，2，3，4，5 GPa隨T的變化;(b)a分別在0，100，200，300，400，500，600，700K隨壓強的變化

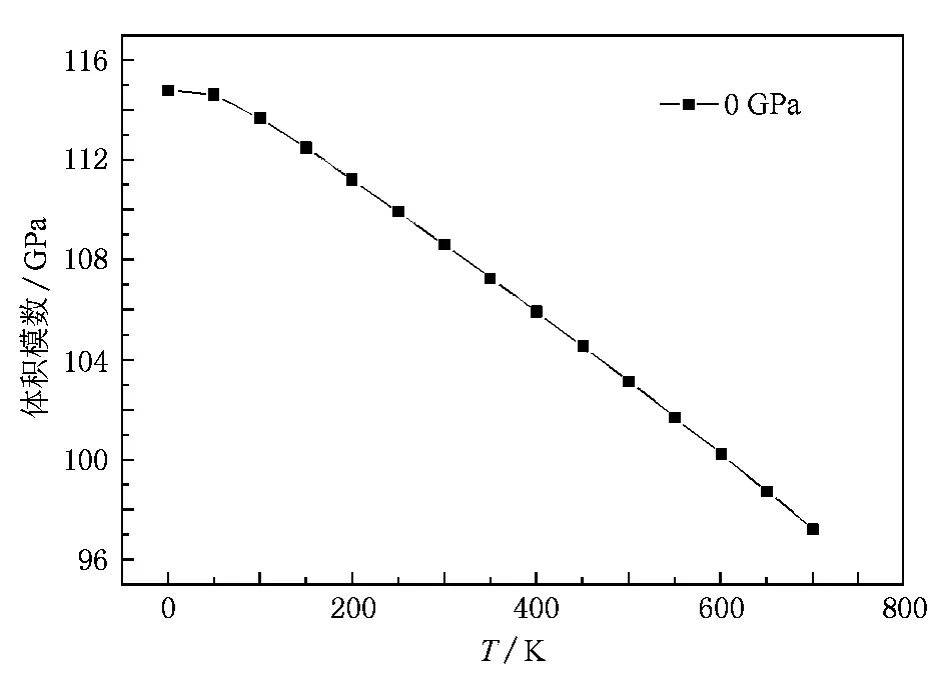
圖5 零壓下Cu3N的體彈模量與T的關系

圖7為Cu3N的α隨T與P的變化曲線.α為固定壓力下平衡體積隨T變化的變化.從圖7中可以看出在給定壓強下，Cu3N的α隨T的升高而增大，低溫時成指數形式增大;在高溫時增大較慢，逐漸趨向于一常數.在給定T下，α隨壓強增大而減小.

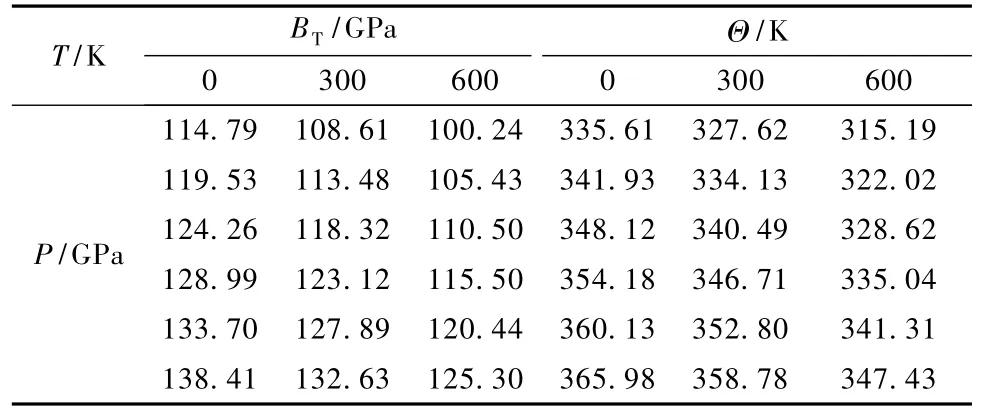
表3 不同T，P下Cu3N的體彈模量BT和Debye溫度Θ

圖6 Cu3N的熱容量與T，P的關系(a)Cp分別在0，1，2，3，4，5 GPa隨T的變化;(b)CV分別在0，1，2，3，4，5 GPa隨T的變化; (c)Cp分別在50，100，200，300，400，500，600，700K隨P的變化

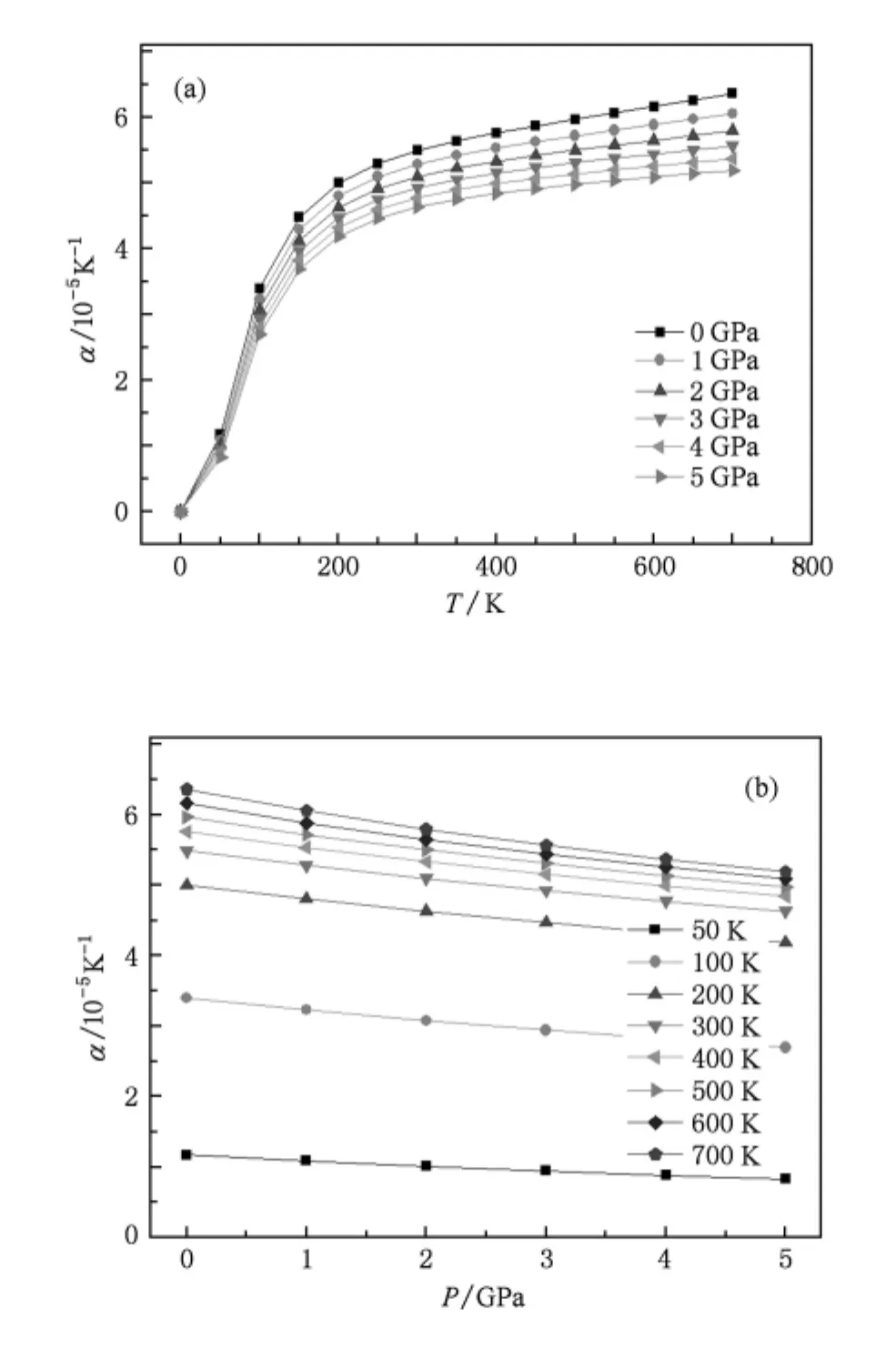
圖7 Cu3N的α與T，P的關系(a)α分別在0，1，2，3，4，5 GPa隨T的變化;(b)α分別在0，100，200，300，400，500，600，700K隨P的變化

4. 結論

本文利用基于密度泛函理論的全勢線性綴加平面波方法計算了Cu3N的基本性質參數和彈性常數;利用準諧Debye模型研究了Cu3N的一些熱力學性質.得到立方反ReO3結構的Cu3N在零溫零壓下當晶格常數a0=3.833時最穩定，與其他實驗結果及計算結果基本一致.通過對晶格的三種形變，計算出彈性常數C11，C12，C44，所得結果與平面波贗勢方法得到的結果一致，表明Cu3N在靜態平衡晶格條件下是穩定的.進一步計算了Cu3N的彈性模量、剪切模量、楊氏模量以及Poisson比.在溫度0—700K，壓強0—5 GPa的范圍內，研究Cu3N的熱力學性質，得到晶格常數隨P增大而減小，隨T升高而增大;體彈模量與Debye溫度隨P增加而變大，隨T升高而減小.在T=300K零壓下，Cu3N的Debye溫度Θ為327.62 K.另外，還得到了CV，Cp，α和T，P的關系，發現熱容隨著P增加而減小，熱脹系數隨P的增大而減小等變化規律.本文對于Cu3N材料的應用能起到一定的促進作用.

［1］Sieberer M，Khmelevskyi S，Mohn P 2006 Phys.Rev.B 74 14416

［2］Moreno-Armenta M G，Pe′rez W L，Takeuchi N 2007 Solid State Sci.9 166

［3］Borsa D M，Grachev S，Presura C，Boerma D O 2002 Appl. Phys.Lett.80 1823

［4］Hansen M，Anderko K 1958 Constitution of Binzry Alloys New York:McGraw-Hill

［5］Maruyama T，Morishita T 1995 J.Appl.Phys.78 4104

［6］Wang J，Chen J T，Miao B B 2006 J.Appl.Phys.100 103509

［7］Borsa D M，Boerma D O 2004 Surf.Sci.548 95

［8］Soto G，Diaz J A，de la Cruz W 2003 Mater.Lett.57 4130

［9］Soukup L，Sícha M，Fendrych F，Jastrabík L，Hubicka Z，Chvostová D，Síchová H，Valvoda V，Tarasenko A，Studnicka V，Wagner T，Novák M 1999 Surf.Coat.Technol.321 116

［10］Pierson J F 2002 Vacuum 66 59

［11］Moreno-Armenta M G，Martínez-Ruiz A，Takeuchi N 2004 Solid State Sci.6 9

［12］Hou Z F 2008 Solid State Sci.10 1651

［13］Yu W，Zhao J G，Jin C Q 2005 Phys.Rev.B 72 214116

［14］Yu W，Li L Y，Jin C Q 2005 J.Mater.Sci.40 4661

［15］Schwarz K，Blaha P，Madsen G K H 2002 Comput.Phys. Commun.147 71

［16］Pan Z J，Zhang L T，Wu J S 2005 Acta Phys.Sin.54 5308(in Chinese)［潘志軍、張瀾庭、吳建生2005物理學報54 5308］

［17］Blaha P，Schwarz K，Madsen G，Kvasnicka D，Luitz J 2008 WIEN2k An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties Vienna University of Technology Inst.of Physical and Theoretical Vienna

［18］Blanco M A，Francisco E，Luaa V 2004 Comput.Phys. Commun.158 57

［19］Chang J，Chen X R，Zhang W，Zhu J 2008 Chin.Phys.B 17 1377

［20］Wang H Y，Cui H B，Li C Y，Li X S，Wang K F 2009 Acta Phys.Sin.58 5598(in Chinese)［王海燕、崔紅保、歷長云、李旭升、王狂飛2009物理學報58 5598］

［21］Amrani B，Achour H，Louhibi S，Tebboune A，Sekkal N 2008 Solid State Commun.148 59

［22］Murnaghan F D 1944 Proc.Natl.Acad.Sci.U.S.A 30 5390

［24］Westbrook J H，Fleischer R L 1995 Intermetallic Compounds: Principles and Practice Volume I:Principles(London:John Wiley，Sons)195—210

［25］Liu N N，Song R B，Sun H Y，Du D W 2008 Acta Phys.Sin. 57 7145(in Chinese)［劉娜娜、宋仁伯、孫翰英、杜大偉2008物理學報57 7145］

PACC:0570C，6220D，7115A

*Project supported by the National Natural Science Foundation of China(Grant No.10974228)，the Research Foundation of Education Bureau of Hebei Province，China(Grant No.2009158)and the Yanshan University Doctor Foundation，China(Grant No.B321).

?E-mail:lish1990@sohu.com

First-principles calculation of elastic and thermodynamic properties of copper nitride*

Li Shi-Na?Liu Yong
(College of Science，Yanshan University，Qinhuangdao066004，China)
(Received 11 January 2010;revised manuscript received 30 January 2010)

A first-principles full-potential linearized augmented plane wave(FP-LAPW)method based on the density functional theory is applied to the study of the static equilibrium lattice structure as well as the elastic constants of the cubic anti-ReO3structural copper nitride(Cu3N).The quasi-harmonic Debye model，in which the phononic effects are considered，is used to investigate the thermodynamic properties of Cu3N.The pressure and temperature dependences of lattice constant，heat capacity and thermal expansion coefficient are successfully obtained.The bulk modulus and Debye temperature are also calculated at different pressures and temperatures.

thermodynamic properties，elastic constants，first-principles，Cu3N

book=701,ebook=701

*國家自然科學基金(批準號:10974228)、河北省教育廳科研基金(批準號:2009158)和燕山大學博士基金(批準號:B321)資助的課題.

?E-mail:lish1990@sohu.com