基于排序函數的區間數非線性規劃模型及其解法
侯勇超趙開斌仇海全
(1巢湖學院數學系,安徽巢湖238000)
(2安徽科技學院理學院,安徽鳳陽233100)
基于排序函數的區間數非線性規劃模型及其解法
侯勇超1趙開斌1仇海全2
(1巢湖學院數學系,安徽巢湖238000)
(2安徽科技學院理學院,安徽鳳陽233100)
首先對區間數的排序方法進行了總結,給出了排序函數的定義,分類和性質,并利用排序函數對一些區間數的排序方法進行了討論.其次,討論了含有區間數系數的非線性規劃模型,利用排序函數將其轉化為一般的非線性規劃問題。最后通過例子說明了方法的簡便性和可行性。
區間數;排序函數;非線性規劃
1 引言
不確定性越來越受到人們的關注,其中應用非常廣泛的是隨機性和模糊性。很多實際問題中,尤其是工程技術、管理決策等領域,由于測量的誤差和主觀因素的影響,往往只能得到一些數據的變化范圍(區間數的形式)。從隨機問題的角度來看,區間數可以視為服從均勻分布的隨機變量,從模糊問題的角度來看,通過模糊集的分解定理和表現定理,可以利用區間數來研究模糊問題。Moore提出區間分析以來,很多學者對區間數的排序問題進行了研究。這些方法大致分為兩類,其一是利用兩個區間數比較的優勢度,可能度或滿意度,并通過判斷矩陣構造排序向量進行排序,優點是盡可能多的保留了區間數的信息,缺點是無法對所有區間數進行排序,這類方法主要用于多屬性決策;其二是將區間數的序通過映射轉化為實數的序關系[1-3],優點是簡單易行計算量小,缺點是轉化過程中會丟失信息。對于區間數優化問題的研究主要集中在區間數線性規劃[4-6],利用區間數的排序將其轉化為普通的線性規劃問題。對于區間數非線性規劃,文獻[7]討論了含有決策風險因子的模型,并用遺傳算法進行了求解。本文首先對區間數排序的方法進行了總結和歸納,提出了排序函數的概念并對已有排序方法進行了分類。然后,討論了區間數非線性規劃的一般模型,利用排序函數將其轉化為一般的非線性規劃模型。最后通過例子說明的方法的可行性和合理性。
2 區間數運算和排序方法
定義1[8]設R為實數域,稱閉區間為區間數,分別稱為區間數的左端點和右端點。R上區間數的全體記作I(R).
Moore(1979)提出如下區間數的排序方法:
定義4[9]設區間數當且僅當
這種方法無法比較區間數有重疊的情況。
Ishibuchi和Tanaka(1990)在研究區間數的線性規劃問題時,提出如下兩種區間數的序關系:
定義5[10]設區間數
以上均為區間數的偏序關系。
劉進生等提出了區間數比較的θ序:
定義7[1]設區間數
區間數的排序還可以借助于區間數的距離實現,首先定義區間數的距離,然后找出問題的極大或極小區間數作為參照,通過計算與參照區間數距離的大小進行排序。
Tran和Duckstein(2002)考慮了區間數每一點的差值,并進行積分得到:

劉華文(2004)對上述距離不滿足正定性進行了改進,定義區間數距離為:
定義10[2]設區間數,則兩區間數的距離為
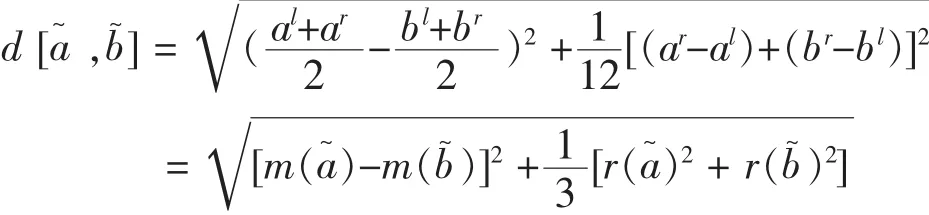
李霞等(2008)對以上距離某些情況下無法區分中點相同,半徑不同的區間數的缺點進行了改進,得到:
定義11[3]設區間數,則兩區間數的距離為
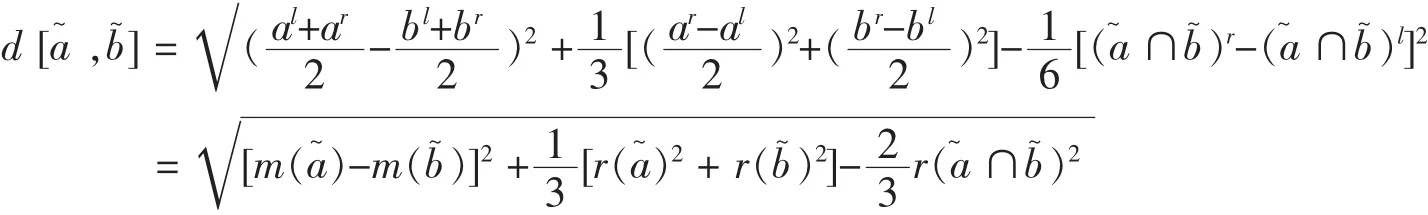
3 區間數排序函數及其分類
借助于區間數距離對區間數排序時,有幾個缺點:第一,只能對極大區間數左側或極小區間數右側的區間數進行排序,無法對所有區間數排序;第二,具體實現時需要事先求出極大或極小區間數;第三,排序方式不靈活,決策者很難根據自己的需要來選擇排序方式.事實上,可以用如下定義的排序函數來對全體區間數進行排序,決策者可根據自己的偏好,來選擇恰當的排序方式.
定義12 若定義在平面區域D?R2上的二元函數z=f(x,y)滿足如下條件:
(1)z=f(x,y)在定義域內連續;
(2)z=f(x,y)在定義域內分別關于x和y單調遞增;
(3)z=f(x,y)在定義域內至少關于一個變量嚴格單調遞增。
則稱z=f(x,y)為區間數排序函數。
將x和y視為區間數的左右端點,則m和r是區間數的中點和半徑。定義12的含義為區間數的一端點不變,另一端點變大時,區間數變大。定義13表明,區間數的中點相同時,用保守型排序函數排序,得到半徑小的區間數較大的結果,而用風險型排序函數得到半徑大的區間數較大的結果。這些都是與我們的直觀認識相符的。
性質2保守型排序函數和風險型排序函數均可對中點相同的區間數辨別大小,結果相反。
性質3折中型排序函數均存在對于個別中點相同,半徑不同的區間數無法辨別大小的情況。
證明:設z=f(x,y)=g(m,r)為折中型排序函數。由復合函數的連續性,z=g(m,r)為連續函數。由折中型排序函數的定義,?m0,z=g(m0,r)關于r無嚴格單調性。則對m0,?r1,r2(r1<r2)使得g(m0,r1)=g(m0,r2)。此時,由于區間數<m0,r1>和<m0,r2>對應的排序函數值相同,故z=f(x,y)=g(m,r)無法辨別它們的大小。
若z=f(x,y)存在偏導數,則有如下結論:
定理1設z=f(x,y)在平面區域D?R2上存在偏導數,若有則z=f(x,y)為排序函數。
定理2設z=f(x,y)為區間數排序函數,且有偏導數,則z=f(x,y)為保守型排序函數的充分條件為<0,z=f(x,y)為風險型排序函數的充分條件為
例1定義7中的排序方式可看作以z=f(x,y)=(1-θ)x+θy,(0≤θ≤1)為排序函數構造的區間數的序。其中=2θ-1,當時,z=f(x,y)為保守型排序函數;當時,z=f(x,y)為風險型排序函數;當為折中型排序函數,此時無法辨別中點相同半徑不同的區間數。
用區間數距離定義的序關系可看作用相應的排序函數實現,以下用區間數[0,0]為參考點,對所有非負區間數(即左端點為非負實數的區間數)排序為例說明。
例2用定義8中距離排序相當于用以下排序函數排序

例3用定義9,10,11中距離排序相當于用以下排序函數排序
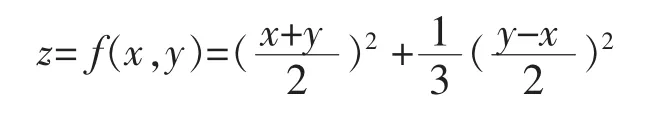
例4設f(x,y)=ax3+by3,(a>0,b>0),可得f(x,y)分別關于x,y單調遞增,則f(x,y)為I(R)上的排序函數。并且,當a≤b時,f(x,y)為風險型排序函數;a>b時,f(x,y)為折中型排序函數。
例5設f(x,y)=ax·by,(a>1,b>1),可得,則f(x,y)為I(R)上的排序函數。并且a<b時,f(x,y)為風險型排序函數;a>b時,f(x,y)為保守型排序函數;a=b時,f(x,y)為折中型排序函數。
4 區間數非線性規劃的模型
以上定義的排序函數可以用來求解如下區間數非線性規劃模型[11]:

設z=f(x,y)為I(R)上的排序函數,則上述模型可轉化為一般的非線性規劃模型:

其中Zl(X),Zr(X)分別為目標函數左端點和右端點,S為問題的可行域。
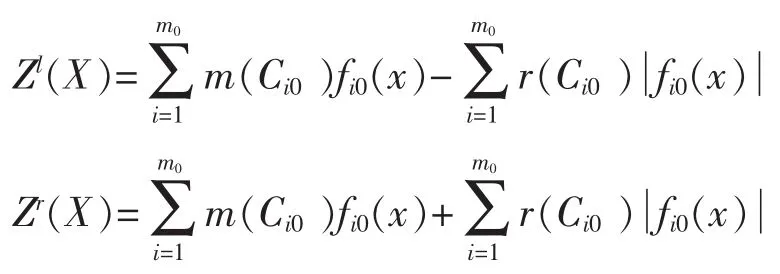
在解決問題的過程中,決策者可以根據自己的偏好靈活選擇排序函數z=f(x,y)
例6考慮下面的問題
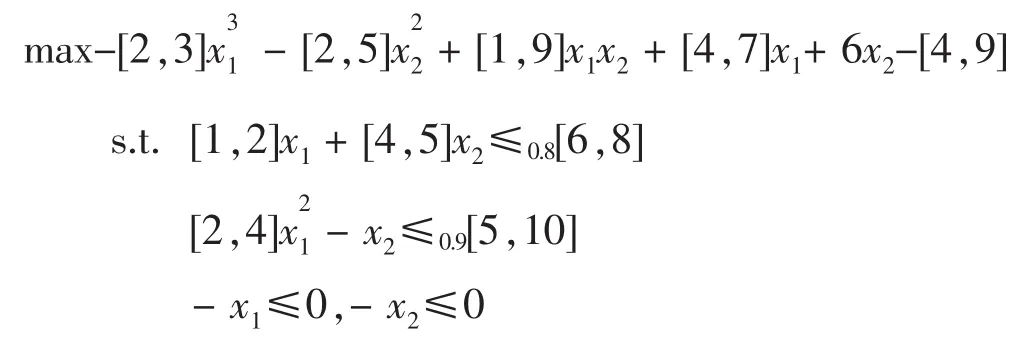
解:設z=f(x,y)為I(R)上的排序函數,則問題轉化為
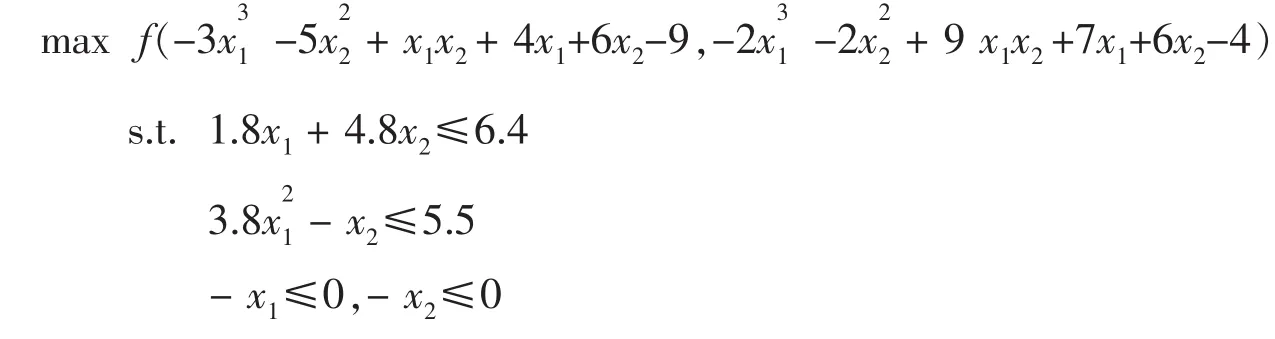
取排序函數為f(x,y)=ax·by,(a>1,b>1),不妨a=1.1
當b=1.05時,排序函數為保守型排序,求得最優解為[-6.0992,13.8236].
當b=1.1時,排序函數為折中型排序,最優解為[-6.4300,14.0625].
當b=1.15時,排序函數為風險型排序,最優解為[-6.6268,14.1463].
下表給出了b取不同值時,最優解的情況:
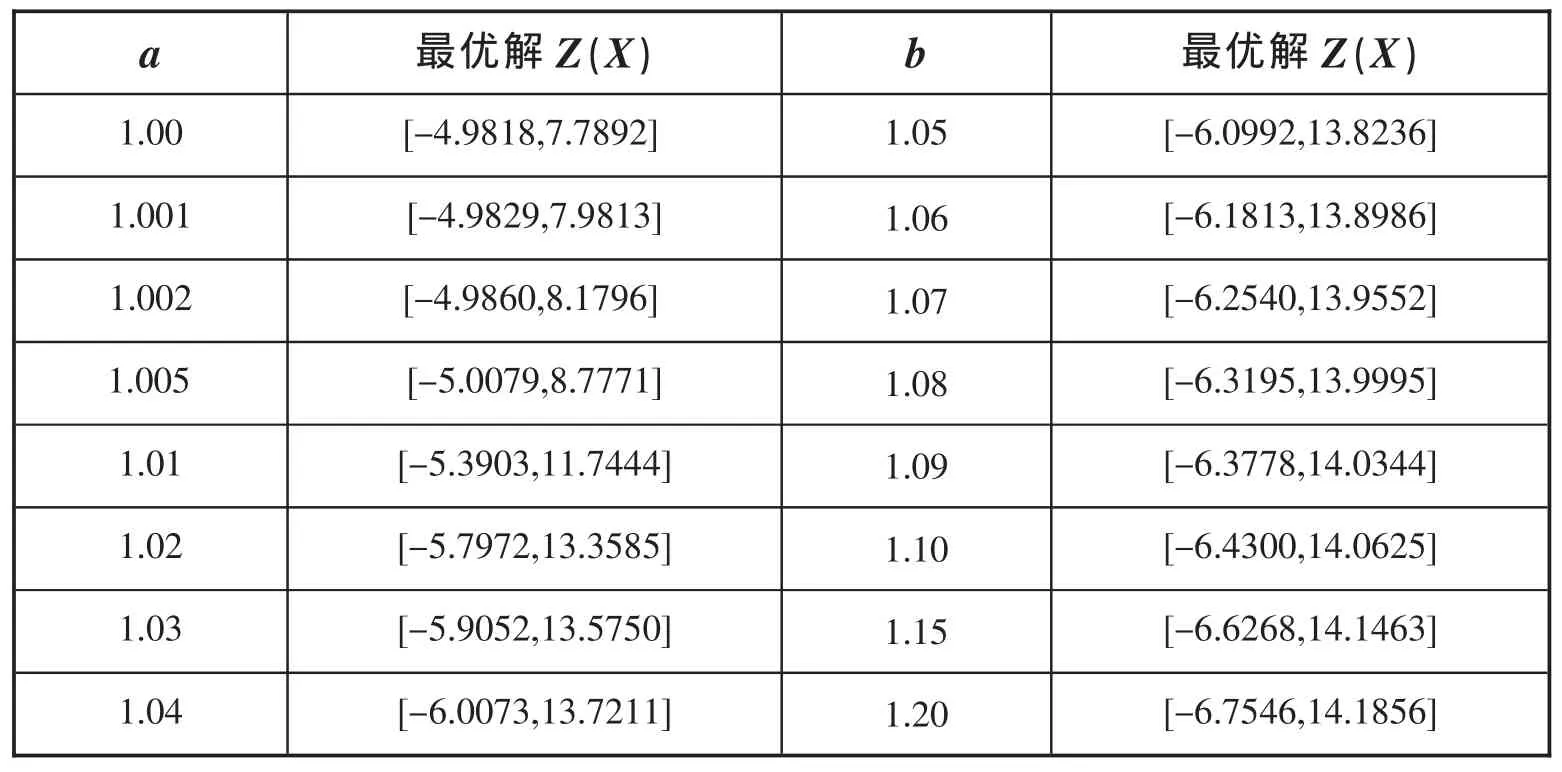
表4 .1 a=1.1,b取不同值時,原優化問題的最大區間數的取值情況
從以上結果可以看出,風險型排序注重右端點的最大化程度較大,隨著b的增大,這種程度變大;保守型排序風險型排序注重左端點的最大化程度較大,隨著b的減小,這種程度變大;以上折中型排序的結果即為中點最大。
5 結論與展望
本文首先總結了區間數的排序方法,提出了區間數排序函數的概念,研究了排序函數的分類方法和相關性質。然后,將區間數排序函數應用于區間數非線性規劃問題的求解中,利用排序函數將其轉化為普通的優化問題。最后,通過例子說明了決策者可根據自己的需要選擇排序函數來解決區間數的優化問題。對區間數排序函數還可以繼續進行更加細致的分類和研究,這將有利于決策者選擇更合適的排序函數解決問題。
[1]劉進生,王柱緒.區間數排序[J].工程數學學報,2001,18(4):103-109.
[2]劉華文.基于距離測度的模糊數排序[J].山東大學學報,2004,39(2):30-36.
[3]李霞,張紹林,張淼,劉華.基于新距離測度的區間數排序[J].西華大學學報,2008,27(1):87-90.
[4]劉新旺,達慶利.一種區間數線性規劃的滿意解[J].系統工程學報,1999,14(2),123-128.
[5]郭均鵬,吳育華.區間線性規劃的標準型及其求解[J].系統工程,21(3),79-82,2003.
[6]胡寶清.區間目標規劃與模糊目標規劃[J].模糊系統與數學,2004,18:218-223.
[7]蔣崢,戴連奎,吳鐵軍.區間非線性規劃問題的確定化描述及其遞階求解[J].系統工程理論與實踐,2005,(1):110-116.
[8]Alefeld R,Herzberger J.Introduction of interval computations.Academic Press,New York,1983.
[9]R.E.Moore,Method and Application of Interval Analysis,SIAM,Philadelphia,1979.
[10]Ishibuchi H,Tanaka H.Formulation and analysis of linear programming problem with interval coefficients[J].Journal of Japan Industrial Management Association,40(5),320-329,1989.
[11]侯勇超,曹炳元.一種區間系數非線性規劃的模型與求解方法[A].中國運籌學會第八屆學術交流會論文集,2006.
Abstract:In this paper,the definition of ordering function is proposed.First,we study its properties and classification.Next, the ranking function is used to solve interval nonlinear programming problems by converting them to classic ones.Finally,an example illustrates the feasibility and simplicity of the method.
Key words:Interval Number;Ranking Function;Nonlinear Programming
責任編輯:宏彬
STUDY OF INTERVAL COEFFICIENT NONLINEAR PROGRAMMING BASED ON RANKING FUNCTION
HOU Yong-chao1ZHAO Kai-bin1QIU Hai-quan2
(1Department of Mathematics,Chaohu University,ChaohuAnhui238000)
(2College of Science,Anhui Scoence and Technology University,Fongyang Anhui 233100)
O159
A
1672-2868(2010)03-0005-06
2010-02-23
巢湖學院基金項目(項目編號:XLY-200903),安徽省教育廳重點項目(項目編號:KJ2010A242)。
侯勇超(1982-),男,山東聊城人,助教,研究方向:模糊優化,數值方法。

