G ira rd Q uan ta le范疇中的乘積
李 靜,泥立麗,張文倩
(1.泰山學院數學與系統科學學院,山東泰安 271021;
2.肥城市汶陽中心小學;3.肥城市汶陽中心中學,山東肥城 271606)
G ira rd Q uan ta le范疇中的乘積
李 靜1,泥立麗1,張文倩2,3
(1.泰山學院數學與系統科學學院,山東泰安 271021;
2.肥城市汶陽中心小學;3.肥城市汶陽中心中學,山東肥城 271606)
本文討論了Girard Quan tale范疇的乘積,并且給出了該乘積的結構,同時證明了此范疇中有等化子.
Girard Quantale范疇;等化子;乘積
0 引言
1986年,C.J.M u lvey在研究非交換的C*-代數的譜時首先提出了Q uan tale的概念,從此,Quan tale理論受到了數學家和邏輯學家的廣泛關注,而對于Quantale理論較為系統地介紹始于1990年文獻[1]的出版.在這20多年的發展中,有關Quan tale理論的新觀點、新應用相繼被揭示,如文獻[2-4].而本文結合范疇論[5]的研究方法,借助于文獻[6-7]的一些思想方法,證明了GirardQuan tale范疇中有等化子,并且構造出了Girard Quantale范疇的乘積結構.
下面是一些預備知識,本文未加定義的概念、記號見文獻[1,5].
定義1[1]設Q為完備格,&為Q中滿足結合律的二元運算.若
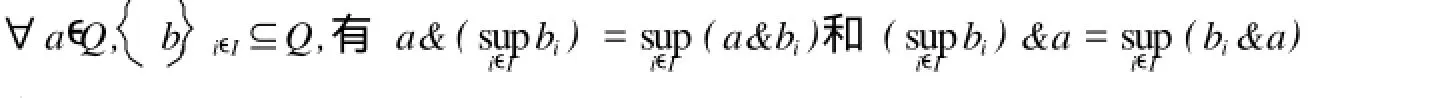
則稱Q為Quan tale.
用0和1分別表示Q的最小元和最大元.
定義2[1]設Q為Quantale,s∈Q,若?a∈Q,有a→ls=a→rs則稱s為Q的循環元.
設Q為Quan tale,d∈Q,若?a∈Q,有(a→ld)→rd=a=(a→rd)→ld,則稱d為Q的對偶元.
若d既為Q的循環元又為Q的對偶元,則稱d為Q的循環對偶元.
定義3[1]設Q為Quantale,若Q含有循環對偶元d,則稱Q為Girard Quan tale.
定義4 所有僅含一個循環對偶元的Girard Quantale(以下僅稱為Girard Quantale)和保循環對偶元的Quantale同態(以下簡稱為Girard Quanta le同態)構成的范疇稱為Girard Quantale范疇,記作GQuant,用Ob(GQuan t)表示GQuant-對象類,用M or(GQuant)表示GQuant-態射類.
定義5[5]設C是一個范疇,f,g:A→B是C-態射.二元組(E,e)稱為f,g在C中的一個等化子,若E∈O b(GQuant)且
(1)e:E→A是C-態射;
(2)f°e=g°e;
(3)?E’∈O b(C),?e’:E’→A∈M or(C)使得f°e’=g°e’,則存在唯一的C-態射?-e:E’→E使得e’=e°-e,
即下圖可換:
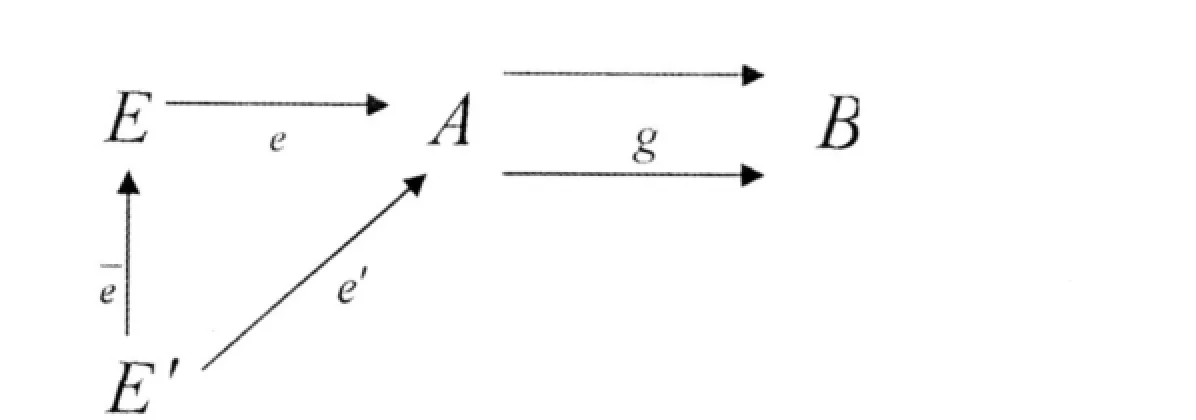

1 Girard Quantale范疇中的乘積結構
命題1 設Q1,Q2為Girard Quan tale,f1,f2是從Q1到Q2的Girard Quan tale同態,則f1和f2有等化子.


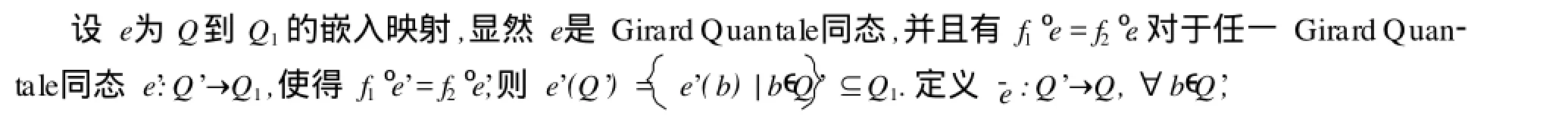
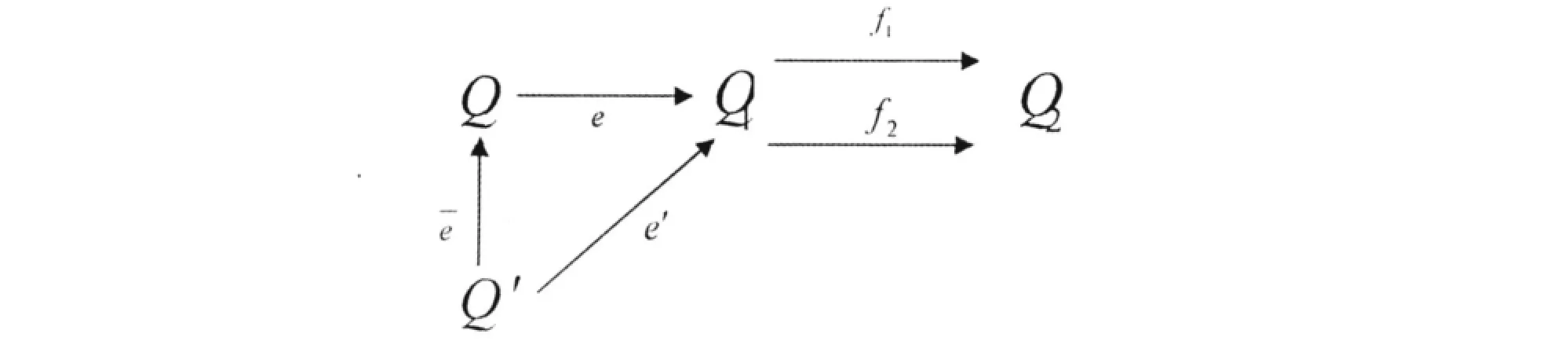
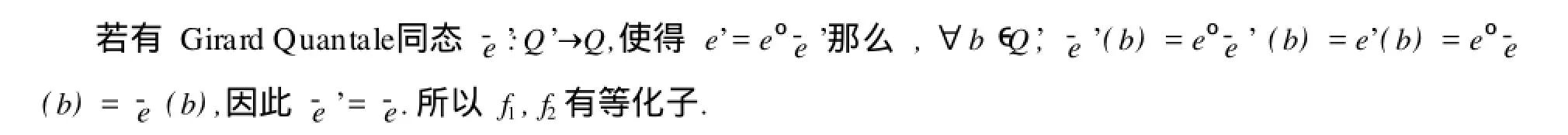
注1 命題1中的e是Girard Quan tale范疇中的正則單態射,(Q,e)為Q1的子對象.
命題2 Girard Quan tale范疇有有限乘積.

設π1,π2分別是P×Q到P,Q上的投射,易知π1,π2是Girard Quantale同態.下面說明(P×Q,π1
×π2)是P,Q在范疇GQuant中的乘積.
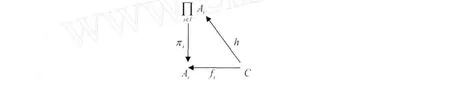
?S∈Ob(GQuan t),f:S→P,g:S→Q是Girard Quantale同態.取h:S→P×Q為:?s∈S,h(s)=(f(s), g(s)).顯然f=π1°h,g=π2°h.如下圖所示:
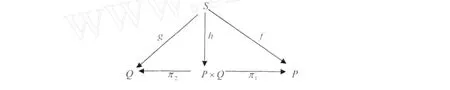
下面驗證h是Girard Quan tale同態.
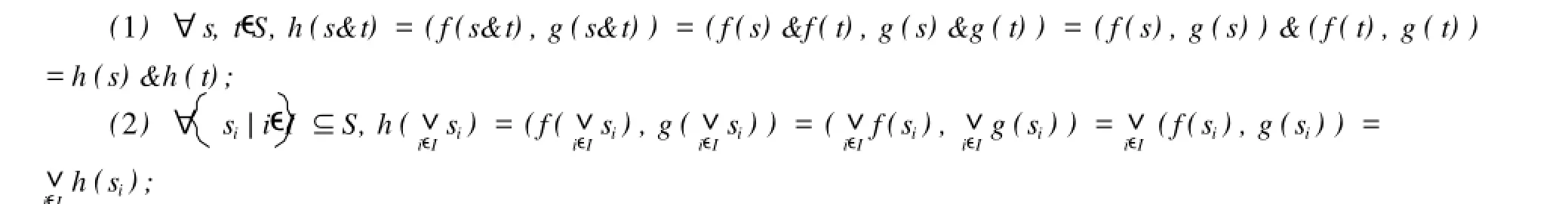
(3)設d∈S為S中的循環對偶元,由于f,g都為Girard Quantale同態,所以f(d)=d1∈P,g(d)= d2∈Q,分別為P,Q中的循環對偶元,所以h(d)=(f(d),g(d))=(d1,d2)就為P×Q中的循環對偶元.
故h是保循環對偶元的Quantale同態.
下證這樣的態射h是唯一的.假設還存在h’使得f=π1°h’,g=π2°h’,那么?s∈S,h(s)=(f(s),g(s)) =(π1°h’(s),π2°h’(s))=h’(s),所以h=h’.
故P×Q是P與Q的乘積.
下面我們把Girard Quantale P和Q的笛卡兒積P×Q推廣到任意Girard Quantale族Qii∈I上,如下定義笛卡兒乘積Πi∈IQi上的運算:其中的序關系采用點式序.笛卡兒乘積的“&”運算是按分量做“&”運算,Πi∈IQi中的循環對偶元是這樣的一個元素:它的每個分量為循環對偶元.由此得到下面的命題.

定理1 Girard Quan tale范疇有乘積.

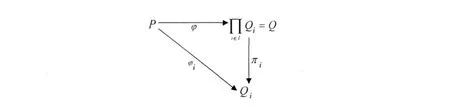
由于φi為Girard Quan tale同態,所以易知φ也為Girard Quan tale同態.

所以Πi∈IQi是Girard Quan tale范疇的乘積.
[1]Rosenthal I.Quantales and their app lications[M].New York:Longman Scientific&Technical,1990.
[2]王偉華,吳洪博.非交換BR0-代數與其上的Quan tale[J].計算機工程與應用,2008,44(25):43-45.
[3]張小紅,魏萍.DR0-代數:由DeM organ[N].代數導出的正則剩余格[J].數學進展,2008,37(4):499-511.
[4]梁少輝,趙彬.連續Quan ta le及其范疇性質[J].陜西師范大學學報(自然科學版),2008,36(5):1-5.
[5]Herrlich H.Category theo ry[M].Berlin:Heldermann Verlag,1979.
[6]樊太和.分子格范疇中的積運算[J].科學通報,1986,31(4):243-247.
[7]徐曉泉.完全分配格范疇中的乘積和上積及其結構[J].科學通報,1990,35(9):623-646.
The Product in the Category of G irard Quan ta le
L IJing1,N ILi-li1,ZHANGW en-qian2,3
(1.SchoolofM athematicsand System s Science,Taishan University,Tai’an,271021;
2.W enyang Central Prim ary School;3.W enyang CentralM idd le Schoo l,Feicheng,271606,China)
In thispaper,the p roduct in the category of Girard Quantale is considered,and its conform ation isgiven.A t the sam e tim e,the theo rem isp roved,which the category of Girard Quantale has the equalizer.
the catego ry of Girard Quantale;the equalizer;the p roduct
O 153.1
A
1672-2590(2010)03-0018-04
2010-04-10
李 靜(1981-),女,山東肥城人,泰山學院數學與系統科學學院講師.

