指定與不指定備選點的配送中心選址-庫存模型研究

王 非，王麗萍，孫浩杰

（1.長安大學 經濟管理學院，西安 710064；2.西安外國語大學 人文地理研究所，西安 710061）

指定與不指定備選點的配送中心選址-庫存模型研究

王 非1,2，王麗萍1，孫浩杰1

（1.長安大學 經濟管理學院，西安 710064；2.西安外國語大學 人文地理研究所，西安 710061）

針對物流企業經常遇到的配送中心只能在指定的備選點中選擇的限制，將固定建設成本風險共擔選址－庫存問題擴展為不指定與指定備選點的可變建設成本配送中心選址-庫存模型，構建了二次非線性0-1整數規劃模型。結合粒子群算法的特點，分別設計J×J矩陣與I×J矩陣為不指定備選點和指定備選點的可變建設成本配送中心選址—庫存模型的初始粒子。在粒子群算法思路、流程指導下，用C＋＋編程，通過C++builder運算。采用Hakimi文章中算例計算，并對運輸成本系數β、庫存成本系數θ進行敏感性分析。

物流管理；選址；粒子群；配送中心

1 選址-庫存模型綜述

選址問題包括離散選址與連續選址問題兩大類。中值模型[1]、覆蓋模型[2]、中心模型[3]是離散選址問題的三大基本模型。絕大多數配送中心選址模型都是基于中值模型擴展而來，但這些模型均未將物流企業庫存成本考慮在內。自上世紀80年代以來，很多學者對選址-庫存問題進行了深入研究，多數學者將重點放在結合選址問題的庫存模型上，更接近于庫存問題的擴展研究。至上世紀90年代末，有部分學者開始對結合庫存的選址問題進行深入探討。Nozick與Turnquist在配送中心選址模型中不僅考慮交通成本,而且考慮了供應鏈管理中庫存成本的影響作用，將安全庫存成本包含在固定裝卸成本中，建立起單級庫存-選址模型[4]。Nozick與Turnquist擴展上述模型，從單級演化到兩級，確定各中心的庫存水平及區位，以權衡顧客服務水平與單位產品成本[5]。

Shen與Daskin以中值模型為基礎，構建了無配送能力限制的風險共擔選址-庫存模型 (LMRP）[6]。作者應用Eppen的研究結果，即在配送中心設立庫存成本（持有成本與安全庫存成本）比在各零售商分散設置的庫存總成本小[7]，利用風險共擔策略將安全庫存設在配送中心，進而采用EOQ經濟訂貨批量模型計算配送中心的最優訂貨量，在此基礎上構建了LMRP選址－庫存模型。

Shen與Daskin構建LMRP選址－庫存模型如下：

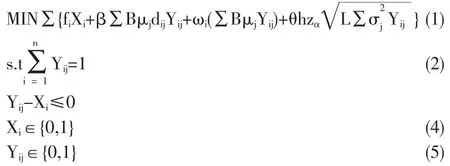
模型參數、輸入變量及目標函數與約束條件意義請參見參考文獻[6]。

2 不指定備選點的基于可變建設成本的配送中心選址-庫存模型構建

在實際中，物流企業常常根據所要服務的零售商的區位、數量及需求量確定配送中心的建設規模，從而決定建設、租用每個配送中心的成本。而LMRP模型將所有配送中心的建設成本設為常量，不僅與實際情況不符，而且會導致資金資源的巨大浪費。

在Daskin和Shen構建的LMRP二級選址－庫存模型基礎上，將配送中心固定費用（每年修建或租用費用）由固定參量轉化為可變參量。

基本假設：

配送中心建設成本為配送中心規模的線性函數；配送中心無配送能力限制；物流網絡中，所有零售商需求必須被滿足，且只能由一個配送中心為其供貨；零售商只能由配送中心供貨；配送中心為本地零售商供貨的運輸成本為0。

將配送中心建設成本視為配送中心規模的線性函數f(x)=fi+mx，其中x為配送中心的期望平均庫存量，包括該配送中心的安全庫存量與訂貨量，m為配送中心建設成本系數。

配送中心運作成本包括訂貨成本、運輸成本、平均庫存成本。

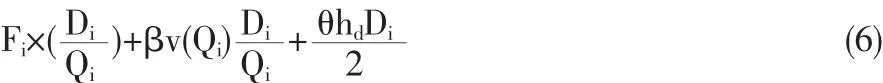
上式第一項為配送中心訂貨成本，第二項為從供應商到配送中心的上游運輸成本，第三項為平均庫存持有成本。Qi為配送中心i的平均訂貨量，將Qi代人式（6）對Qi求導并令其等于0，得最優訂貨量

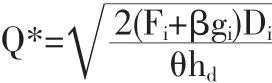
基于可變建設成本的配送中心選址－庫存模型為：

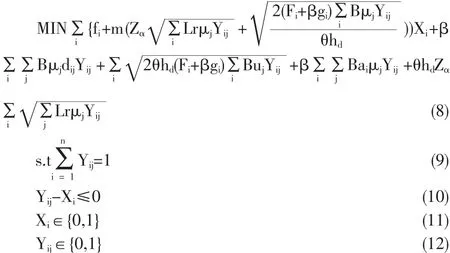
其中：

hd為配送中心單位庫存成本；Fi為配送中心每次訂貨的固定成本；

m為配送中心建設成本系數；

式（8）目標函數中第一項為配送中心建設成本，第二項為配送中心到零售商的下游運輸成本，第三項與第四項之和為配送中心運營成本，第五項為安全庫存成本。

約束條件式（9）表示每個零售商需求都被滿足，且只能由一個配送中心滿足；約束條件式（10）表示零售商只能配送中心供貨。 約束條件式（11）、（12）表示、為 0－1 變量。

3 指定備選點的基于可變建設成本的配送中心選址－庫存模型構建

指定備選點的基于可變建設成本的配送中心選址－庫存模型假設配送中心只能在指定備選點中修建，其他模型假設與不指定備選點的模型相同。在特定網絡中，已知備選點區位、各零售商需求與網絡距離矩陣，給定建設成本系數、運輸成本系數、庫存成本參數，求解包括配送中心建設成本、運作成本、運輸成本、安全庫存成本在內的總成本最小值、建設配送中心的最佳區位以及配送中心給零售商配送的最優路徑。

指定備選點的基于可變建設成本的配送中心選址－庫存問題優化模型與不指定備選點的選址－庫存問題優化模型的目標函數相同，主要區別在于增加了一項約束條件。

約束條件（13）表示備選點的數量少于總的節點數。P為指定備選點數量。

4 粒子群算法求解

粒子群優化算法是Kennedy和Eberhart[7]于1995年提出的一種全局優化進化算法,其思想來源于對鳥群捕食行為的研究。鳥群在隨機搜尋食物時，如果搜尋區域里只有一塊食物，那么找到食物的最簡單有效策略就是搜尋目前離食物最近的鳥的周圍區域。

求解基于可變建設成本的配送中心選址－庫存問題的粒子群算法設計的關鍵在于可行解設計【8】。對指定備選點的優化模型粒子群算法設計流程和思路與不指定備選點的設計流程與思路基本相同，不同之處在于粒子的設計。不指定備選點的粒子可表示為J×J矩陣形式，而指定備選點的粒子則表示為I×J矩陣形式，其中I＜J。從不指定備選點的J行中指定I行作為備選配送中心，其它規定與不指定備選點的粒子設計相同。每列隨機生成的1只能在第1至第I間產生，而不能在第1行與第J間產生。圖1表示指定備選點數量為3的粒子，粒子只有3行，表示只能從指定的3個零售商中選擇配送中心區位。最上端隨機生成數組（3，3，3，2，2，2，2…3）表示在各自列的第3，3，3，2，2，2，2 … 3行 生 成 1， 則 X2、X3為1。

依據Jiang和Luo文獻中的粒子群算法收斂性分析，為使粒子位置的期望與位置方差收斂[9]，結合相關文獻參數，對Hakimi、Daskin和 Shen的文章中的 10節點、49節點、88節點算例進行近百次測試，最終確定針對可變建設成本的配送中心選址-庫存問題的粒子群算法參數[8]。基于可變建設成本的配送中心選址－庫存問題的粒子群算法的各項參數見表1。

表1中參數不僅滿足Jiang和Luo文獻中算法收斂的所有條件，而且經過多次測試取得不錯計算結果。

圖1 指定備選點的粒子設計示意圖

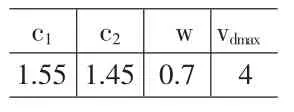
表1 粒子群算法各參數

表2 Hakimi的10節點算例各零售商需求

表3 10節點算例中其它模型參數

5 數值算例

針對指定與不指定備選點的基于可變建設成本的配送中心選址－庫存模型，設計粒子群算法，用C＋＋語言編程，通過C++builder進行運算。因篇幅所限，僅對Hakami文章中10節點算例進行計算和分析。Hakimi文章中算例為10節點網絡，各輸入參數見表2、表3、表4。

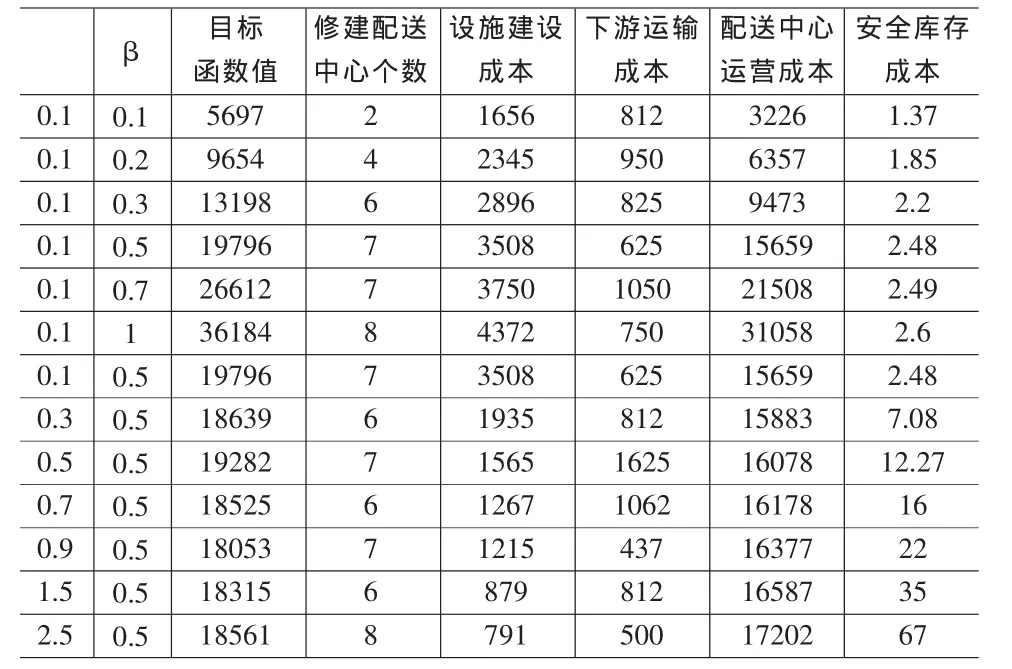
表4 10節點網絡計算結果

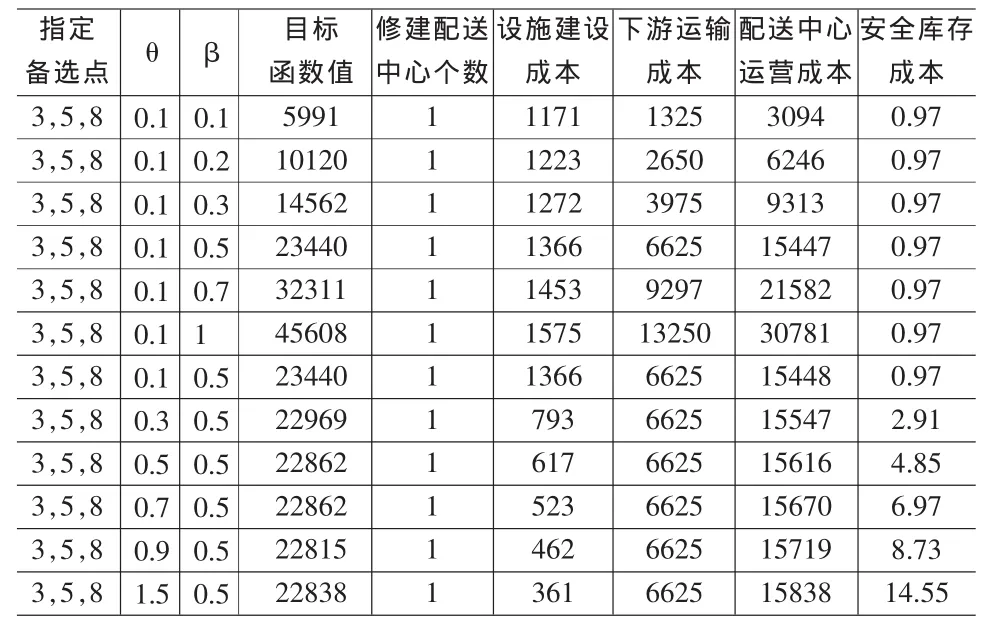
表5 指定備選點10節點計算結果

5.1 計算結果

在模型其它參數確定情況下，對影響模型目標值的因素進行敏感性分析。不指定備選點的基于可變建設成本的配送中心選址－庫存模型10節點算例計算結果見表4。

利用Hakimi文獻中10節點網絡算例，以節點3、5、8為指定備選點，求解指定備選點的基于可變建設成本的配送中心選址-庫存模型，計算結果見表5。

指定備選點為節點3、5、8的 10節點算例決策變量部分計算結果如下：

當 θ＝0.1，β=0.1 時

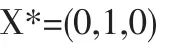
即在節點5修建配送中心。

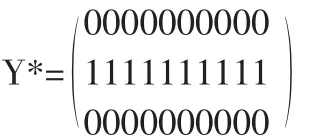
即配送中心5為所有零售商配送。

5.2 討論與分析

對上述結果進行分析可知，在其它參數不變條件下，運輸成本系數β與庫存成本系數θ的改變對模型優化結果有顯著影響。對運輸成本系數β、庫存成本系數θ進行敏感性分析，可得以下結論：

5.2.1 運輸成本系數β變化對優化結果影響分析

(1)庫存成本系數θ不變，運輸成本系數β與修建配送中心的個數呈正相關關系。表4顯示，當運輸成本系數β由0.1增長到1時，配送中心個數由2個增加到8個。

(2)庫存成本系數θ不變，運輸成本系數β與目標函數值、配送中心建設成本、配送中心運營成本以及安全庫存成本即呈正相關關系。根據表4計算結果，當運輸成本系數β由0.1增長到1時，目標函數值由5696增加到36184，增幅為6.21倍；配送中心建設成本由1656增長到4372，增幅為2.67倍；配送中心運營成本由3226增長到31058，增幅為9.62倍；安全庫存由1.37增長到2.6，增幅1.9倍。

為求得模型最優值，如運輸成本增加，配送中心建設成本相對減小，故修建配送中心的個數增加。隨著β增加，配送中心個數增加，根據安全庫存成本項公式，安全庫存成本增加。

5.2.2 庫存成本系數變化對優化結果影響分析

(1)運輸成本系數β不變，庫存成本系數θ與配送中心建設成本呈負相關關系。表4顯示，庫存成本系數θ由0.1增加到2.5，配送中心建設成本由3508減少到791。

(2)運輸成本系數β不變，庫存成本系數θ與配送中心運營成本、安全庫存成本呈正相關關系。表4顯示，庫存成本系數θ由0.1增加到2.5，配送中心運營成本由15659增長到17202，增長1.1倍；安全庫存成本由2.48增加到67，增長27倍。

運輸成本系數與庫存成本系數反映了運輸及商品庫存成本在總成本中占用比重的大小，決定目標函數值，同時決定配送中心的修建數量及相應成本。

5.2.3 指定備選點模型計算結果分析和與不指定備選點模型計算結果比較

(1)庫存成本系數、運輸成本系數對指定備選點模型目標值的影響與不指定備選點模型的基本相同。

運輸成本系數β與配送中心建設成本、配送中心運營成本以及安全庫存成本即呈正相關關系。選取10節點算例中的3、5、8為指定備選點，如表5顯示，當庫存系數θ為0.1時，運輸成本系數β由0.1增加到1，配送中心建設成本由1171增加到1575；配送中心運營成本由3094增加到30781。因只建一個配送中心，安全庫存成本不變，為 0.97。

庫存成本系數θ與配送中心建設成本呈負相關關系；庫存成本系數θ與配送中心運營成本、安全庫存成本呈正相關關系。表5顯示，當運輸成本系數β為0.5時，庫存成本系數θ由0.1增加到1.5，配送中心建設成本由1366減少到361；配送中心運營成本由15448增加到15838；安全庫存成本由0.97增加到14.55。

(2)指定備選點模型目標值不小于不指定備選點模型函數目標值，見表6。

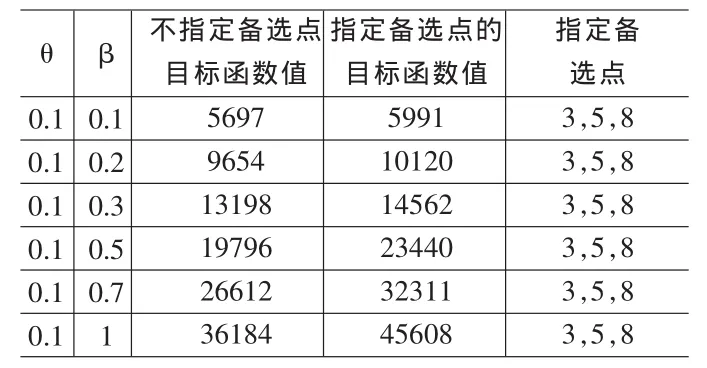
表6 不指定備選點與指定備選點的10節點算例結果比較

6 結論

根據物流企業規劃、經營遇到的實際情況，將固定建設成本風險共擔選址－庫存問題擴展為可變建設成本配送中心選址-庫存模型。同時針對配送中心修建區位的限制，構建了指定備選點的基于可變建設成本的配送中心選址-庫存模型，不指定與指定備選點的選址-庫存模型均為為二次非線性0-1整數規劃模型。結合粒子群算法的特點，分別設計J×J矩陣與I×J為不指定備選點和指定備選點的可變建設成本配送中心選址—庫存模型的初始粒子。在粒子群算法思路、流程指導下，用C＋＋編程，通過C++builder運算。利用Hakimi文章中算例，對運輸成本系數β、庫存成本系數θ進行敏感性分析，依據算例計算結果，認為：運輸成本系數與函數目標值、配送中心數量、建設成本、運營成本以及安全庫存成本正相關；庫存成本系數與配送中心運營成本、安全庫存成本正相關，與配送中心建設成本負相關。指定備選點模型目標值不小于不指定備選點模型函數目標值。

[1]Church,ReVelle.Theoretical and Computational Links between the P-median Location Set-covering and the Maximal Covering Location Problem[J].Geographical Analysis,1976,(40).

[2]Daskin,Stern.A Hierarchical Objective Set Covering Model for E-mergency MedicalService Vehicle Deployment[J].Transportation Science,1981,(15).

[3]Tansel,Francis.Location on Networks:A Survey[J].Management Science,1983,(29).

[4]Nozick and M.Turnquist,IntegratingInventoryImpactsintothe Fixed Charge Facility Location Model for Locating Distribution Centers[J].Transportation Research,1998,34(3).

[5]Nozick T,Turnquist M.A Two-echelon Inventory Allocation and Distribution Center Loacaion Analysis[J].Transportation Research,2001,(37).

[6]Shen Z J,Coullard MC,Daskin M S.A Joint Location-inventory Model[J].Transportation Science,2003,(37).

[7]Eppen H.Effects of Centralization on Expected Costs in a Multilocation Newsboy Problem[J].Management Science,1979(5).

[8]王非.基于可變建設成本的LMRP選址-庫存問題優化研究[D].西安交通大學博士論文，2008.

[8]Jiang M,Luo Y P.Stochastic Convergence Analysis and Parameter Selection[J].Information Processing Letters,2007,(102).

（責任編輯/浩 天）

F224.9

A

1002－6487（2010）18－0177-03

國家社科基金資助項目（07XJY015）；國家自然科學基金資助項目（70871097）；長安大學科技創新基金（CHD2009JC149）

王非，（1972-），男，陜西西安人，博士，副教授，研究方向：物流與供應鏈管理。