用于指導交流電橋實驗調零的矢量數學模型

張瑞斌,秦 穎,李敬安,黃曉明,賴 優

(大連理工大學物理與光電工程學院,遼寧大連116024)

用于指導交流電橋實驗調零的矢量數學模型

張瑞斌,秦 穎,李敬安,黃曉明,賴 優

(大連理工大學物理與光電工程學院,遼寧大連116024)

建立交流電橋的矢量分析模型,用圖示法討論交流電橋實驗,從理論上以更加直觀明了的方式指導調零步驟、進行實驗分析以及計算機模擬.

交流電橋;圖示法;調零

1 引 言

交流電橋電路如圖1所示,電橋達到平衡時,毫伏表示數為零,上下橋臂電位差為零,電橋相對橋臂的復阻抗乘積相等.平衡方程為[1-2]

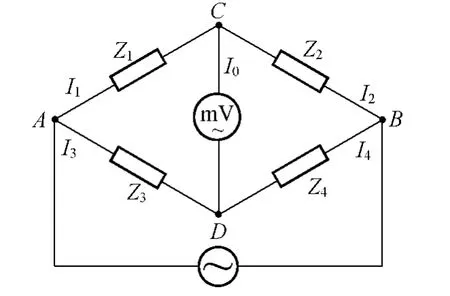
圖1 交流電橋原理圖

由(1)式可知,交流電橋與直流電橋的原理十分相近,但是交流電橋討論的是復阻抗(具有實部和虛部),通常的解決方法是將(1)式分解為分別關于實部和虛部的2個線性方程,這種數學模型很好地體現了交流電橋的本質特征,易于理解.但無法直觀再現交流電橋的平衡過程,難以討論和比較各種設計方案.另外,這種傳統的數學模型很難翻譯成計算機語言,難以數值模擬.

鑒于此,最好的解決辦法是提出新的數學模型.分析平衡方程(1)式,發現交流電橋與直流電橋的區別就是將電阻(標量)擴展為復阻抗(二維矢量).于是嘗試建立交流電橋的矢量分析模型,也就是用圖示法討論交流電橋實驗.

2 實驗選擇標準及優劣判據

電橋實驗設計的優劣判據如下:

1)盡量調節電阻.由于制作工藝上的差異,電容和電感在調節精度和穩定性上都遠遠小于電阻;另一方面,可變電容、電感的最小刻度也無法達到足夠的精度.因而為了提高精度,盡量選用可變電阻以及定值電容和電感.

2)盡量提高調節的速度和測量的精度.

3 運用圖示法討論交流電橋的成功案例

3.1 案例1:調節標準電阻R0和電感L0

先用最簡單的電橋配制方法來闡述圖示法的基本原理.

電路如圖2所示,用j代表虛數單位,則電橋平衡方程可寫成(2)式:其中,R1和R2是比率臂的2個可調電阻,L0為已知電感值,Lx和rx分別為待測電感值和內阻, ω為交流電的圓頻率.此處r0=R0+rL0,其中R0為外加可調電阻,rL0為已知電感的內阻.

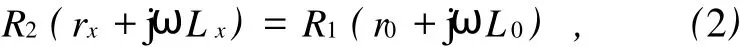
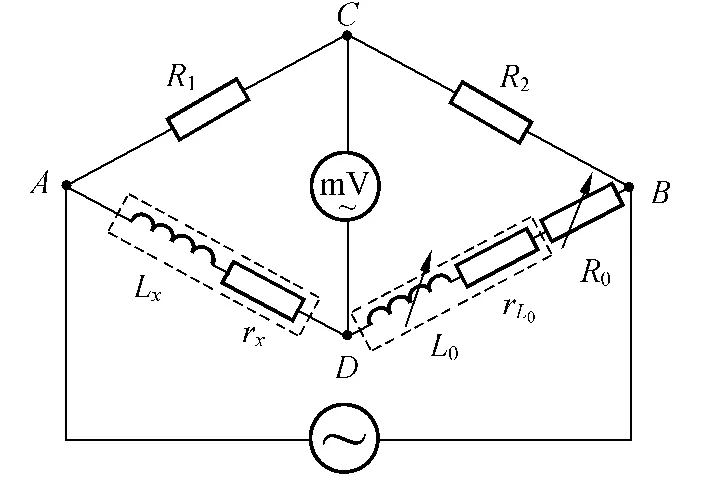
圖2 調節標準電阻和電感

在實際問題中可以對(2)式做如下變形:

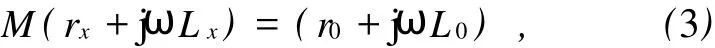
式中,M=R2/R1,在此選為定值(經驗表明,M取0.5～2比較合適).

設矢量OAi代表M(rx+jωLx),OBi代表(r0+jωL0),其中i=1,2….初始時刻狀態所對應的矢量為OA1,OB1,經過調節后OB1與OA1重合.根據交流電橋的平衡方程可以證明(證明略):OAi與OBi差值|AiBi|越小,越接近平衡狀態,當兩矢量差值為零時,毫伏表的示數為零,此時交流電橋達到平衡狀態[1].

利用(3)式設計如下步驟進行調節,矢量變化如圖3所示.

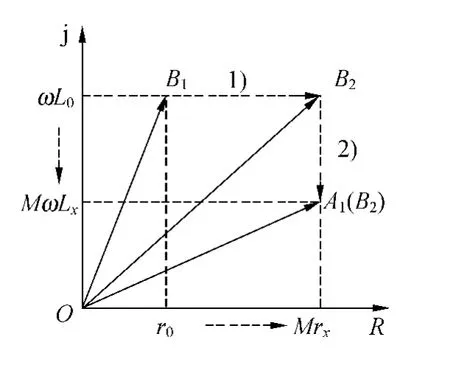
圖3 對應圖2的矢量變化軌跡

1)先調節R0值,就是調節向量OBi的實部,將復阻抗(r0+jωL0)的端點B在直線B1B2上滑移,直到毫伏表示數最小,如圖中矢量OB2的狀態,此時B1B2⊥A1B2,差值最小.

2)再調節L0值,對應于B2沿豎直直線滑移到A1,此時OA1=OB2,毫伏表示數為零,達到了平衡狀態.

3)加大電源電壓,重復實驗,直到所需精度.

上述調零方式十分簡便,物理過程顯得十分清晰.這種調零方式是實驗室里最常見的方法.但是該方法調節了電感L0,明顯違背了上文“盡量調節可變電阻”的約定,需要改進.

3.2 案例2:調節標準電阻R0及倍率M(R2)

分析圖2,發現一共有4個可調量:R1,R2, R0,L0.首先排除L0(不調電感).根據(3)式可知,調節R1,R2改變倍率M(M=R2/R1),為了簡單只需調節其中的一個,在此選調R2.因而確定R2和R0作為可調量,電路如圖4所示.仍采用(3)式,在此M不再是定值,調節R2則M變化.

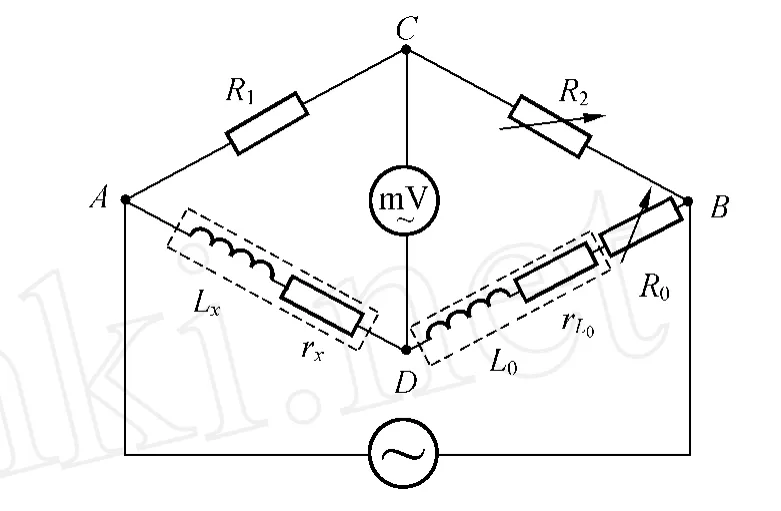
圖4 調節標準電阻R2和R0

用圖示法表示,改變M的值,會使矢量OAi在直線OA上線性地伸縮,調節R0的值,會使矢量OBi端點Bi在直線B1Bi上滑移[1-3].

如圖5所示,調節步驟如下:

1)調節R0使毫伏表示數最小;

2)繼而調節M(M隨R2線性變化),直到毫伏表示數最小;

3)重復步驟1)和步驟2),循環調節直到所需精度.

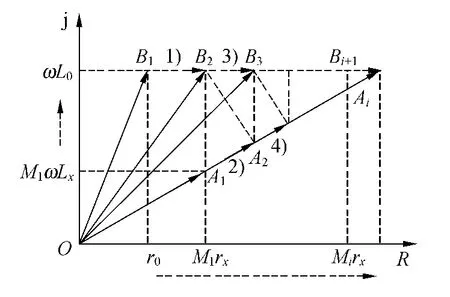
圖5 對應圖4的矢量變化軌跡

很明顯,通過上述調節步驟,OBi與OAi趨于重合,達到電橋平衡.

以上討論中,顯示了圖示法的優越性,將繁雜的交流電橋調節步驟用矢量圖簡易地表達出來,調節步驟清晰,提高了實驗效率.

3.3 案例3:調節被測端標準電阻Rx0及倍率(R2)

在以上2個案例的啟發下找到了更加快速準確的調節方法.設計電路如圖6所示,圖中Lx和rx分別為待測電感和內阻,在待測電感橋臂上串聯可調電阻Rx0,為便于描述,設Rx=rx+Rx0.

平衡方程為

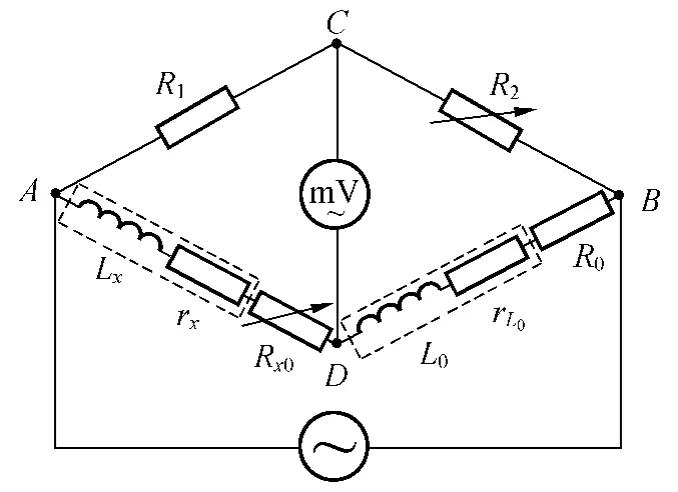
圖6 可調標準電阻接入被測端

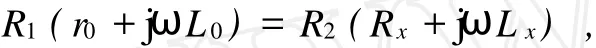
變形后為

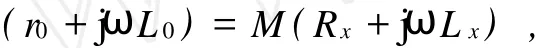
其中M=R2/R1.

設OAi表示矢量M(Rx+jωLx)和OB表示矢量(r0+jωL0);初始時刻的狀態對應于OA1和OB,經過步驟1),2)后對應于OA2,OB,以此類推.

根據上述分析,可得到調零過程如下:

1)調節Rx,使毫伏表示數最小,對應于A1水平滑移到A2,此時BA2與實軸垂直;

2)調節R2,使毫伏表示數最小,對應于A2沿直線OA2滑移到A3,此時OA3⊥BA3;

3)重復上述過程,直到所需精度要求.

矢量變化軌跡如圖7所示.從圖中很容易看出,OAi以更快的速度收斂于OB,此種調零方式比案例2更快地達到平衡.

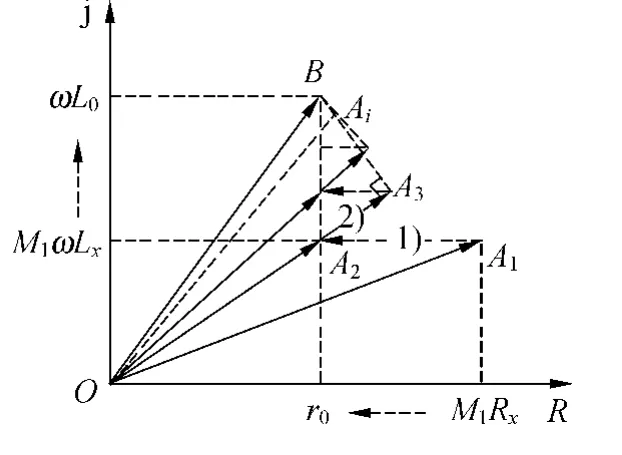
圖7 對應圖6的矢量變化軌跡

從案例2和3可以看出,圖示法挖掘出了交流電橋調零過程中的迭代關系(不斷地尋找垂線).根據垂直矢量點乘積為零,可以寫出對應的迭代算式.采用數值模擬的方法,定量地比較例2和3兩種方法的優劣,結果見表1.為了編程方便,已把電阻和電感無量綱化.設案例2和3中初始狀態相同,均為A=(2,1),B=(1,6)

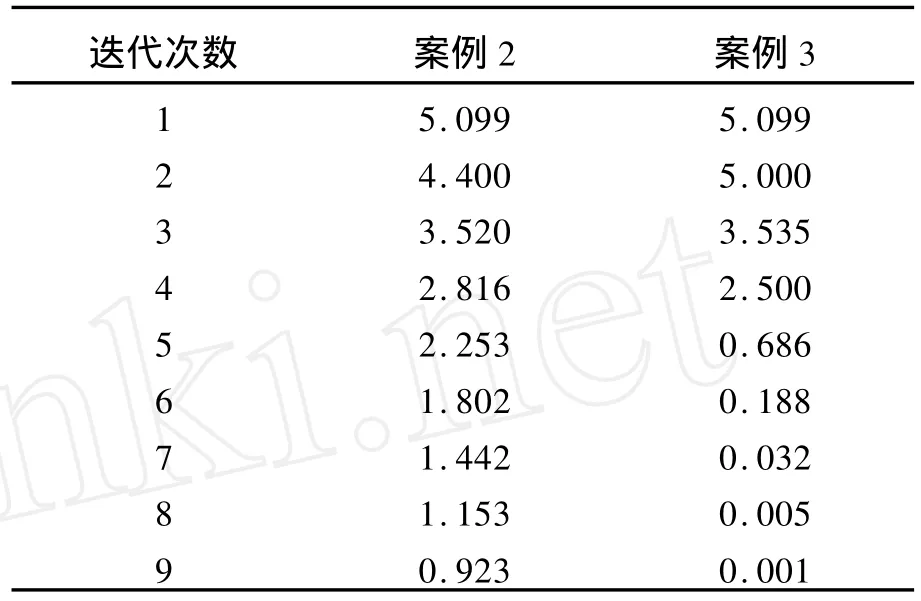
表1 向量A和B差量的模

模擬數據證明案例3所選方法明顯優于案例2,尤其是在精度要求高的情況下,案例3收斂速度快的優點尤為明顯.

比較案例2和3.如果用原來的數學模型來比較上述2種方法優劣非常困難,而圖示法卻一目了然.主要原因就在于圖示法挖掘實驗數據的數學本質(矢量和復數),并運用相應的數學工具建立了恰當的數學模型,能很好地解決有關問題.

3.4 案例4:調節與被測端并聯的標準電阻Rx0及倍率(R2)

下面把圖示法的應用推廣到元件并聯,設計電路圖如圖8所示.

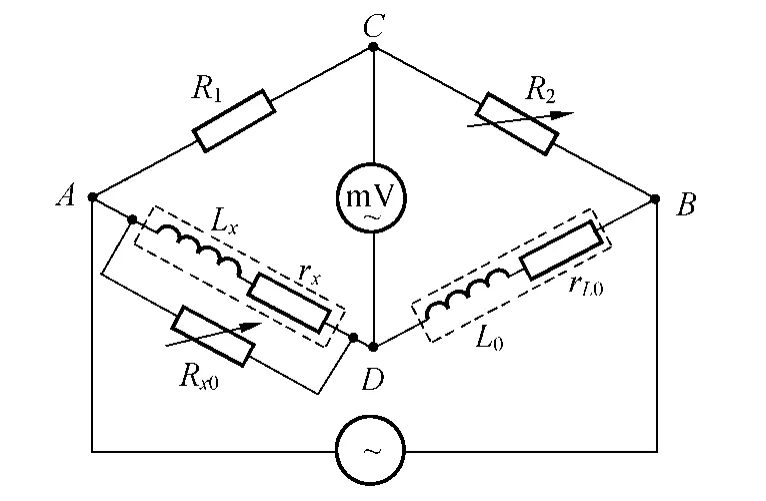
圖8 可調標準電阻與被測端并聯

首先把電橋平衡方程(1)改寫為

在本電路中,平衡方程的具體形式為

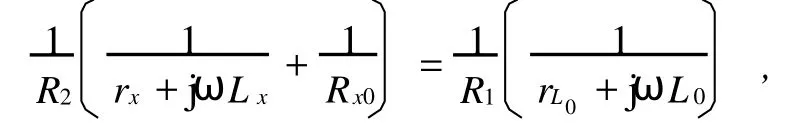
式中,R1和R2為上橋臂2個已知的電阻,Lx和rx為待測的電感和其內阻,L0和rL0為已知的標準電感和其內阻.

設M=R2/R1,則,有2個可調量:依次調節M和 Rx0就可以逼近平衡狀態.

設OAi代表矢量OBi代表矢量

如圖9所示,初始時刻的狀態對應于OA1和OB1,經過以下步驟1)和2)后對應于OA2和OB2,以此類推.

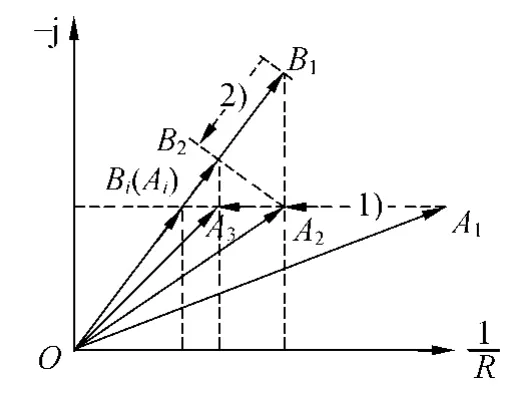
圖9 對應圖8的矢量變化軌跡

具體調節方法如下:

1)調節Rx0使毫伏表示數最小,對應于矢量OA1沿水平直線滑移到OA2,此時A2B1與實軸垂直;

2)調節R2使毫伏表示數最小,對應于OB1沿直線OB1滑移到OB2,此時A2B2⊥OB1;

3)重復步驟1)和2),直到所需精度.

上述調零過程與案例3相似,也可以很快的速度趨于平衡.這種方法最大特點是加入了并聯微調電阻.之所以稱其為微調電阻,是因為Rx0常取一個極大的阻值,導致1/Rx0變化極其緩慢(雙曲線的性質),從而可以實現及其細微的變化.這一點在高精度調節中是很有必要的.另外并聯元件在一定程度上還可以增大系統的抗干擾能力[4-5].

本例再一次說明了圖示法的巨大優勢.由于元件并聯公式較為復雜,用原來解析的方法來研究,復雜度將大大提高,而對于圖示法而言,經過復阻抗取倒數的變換,調零過程依然簡潔明了.

本文選擇了若干含電感的交流電橋討論圖示法的優點,其方法同樣適用于含電容的交流電橋.

[1] 董有爾.大學物理實驗[M].合肥:中國科學技術大學出版社,2006:125-130.

[2] 王愛中.利用直流電橋測量電容[J].物理實驗, 2008,28(4):34-35.

[3] 楊振萍,潘學軍.交流電橋臂的配置與靈敏度[J].四川師范大學學報,1999,22(3):214-218.

[4] 夏寶順.交流電橋有關實驗現象分析[J].物理實驗,2001,21(04):43-44.

[5] 孫伏優.“電感電容對交變電流的影響”演示實驗的改進[J].物理實驗,2008,28(2):21-22.

Vector mathematical model for guiding adjustment of AC bridge circuits

ZHANG Rui-bin,QIN Ying,LI Jing-an,HUANG Xiao-ming,LAI You
(School of Physics and Optoelectronic Technology,Dalian University of Technology,Dalian 116024,China)

A vector mathematical model of AC bridge is set up,and the experiment of AC bridge is discussed by the graphic method.The adjustment procedures,experimental analysis and computer simulation are put forward.

AC bridge;graphic method;zero adjustment

O441.1

A

1005-4642(2010)06-0042-04

[責任編輯:郭 偉]

2009-09-12;修改日期:2009-12-26

2008年大連理工大學大學生創新性實驗計劃項目

張瑞斌(1990-),男,山東濟寧人,大連理工大學物理與光電工程學院2007級本科生.

指導教師:秦 穎(1964-),女,吉林白山人,大連理工大學物理與光電工程學院副教授,博士,從事物理實驗教學與凝聚態物理研究.