參數序限制下最優同變預測區間的改進

劉 燕，肖玉山

(1.吉林農業大學發展學院 基礎部，吉林 長春 130600;2.長春大學 教務處，吉林 長春 130022)

參數序限制下最優同變預測區間的改進

劉 燕1，肖玉山2

(1.吉林農業大學發展學院 基礎部，吉林 長春 130600;2.長春大學 教務處，吉林 長春 130022)

考慮了位置分布族與尺度分布族中，當未知參數含有序限制時，對未知隨機變量的預測區間的問題。利用序限制下最優同變估計量的改進方法，在一定條件下，構造一族改進后的同變預測區間，從而解決了對未知隨機變量同變預測區間的改進問題。

序限制;同變預測區間;位置分布族;尺度分布族;TP2(total positivity of order 2);IERD(integrated expression of risk difference)方法

0 引言

在數理統計當中，設X=(X1，X2，…，Xn)是可觀測隨機向量，Y是未知且不可觀測的隨機變量。設(X，Y)的聯合分布f(x，y;θ)依賴于未知參數(參數向量)θ，基于X的觀測值來預測Y的問題叫做統計預測問題。

統計預測的主要形式之一就是利用X的觀測值給出Y的取值范圍。設l(X)與u(X)是隨機向量X的函數，對給定的實數α(0＜α＜1)，若對任意的θ∈Θ(Θ為參數空間)，有Pθ{l(X)≤Y≤u(X)}≥1-α，則稱［l(X)，u(X)］是具有置信水平為1-α的Y的預測區間。若對任意的θ∈Θ，有Pθ{l(X)≤Y≤u(X)}=1-α，則稱［l(X)，u(X)］是置信水平為1-α的Y的同等預測區間。

預測區間的優良性取決于其評價標準——置信度Pθ(l(X)≤Y≤u(X))和精確度Eθ(u(X)-l(X))，即Y落入預測區間的概率以及預測區間的平均長度。通常我們要在置信水平為1-α的Y的預測區間當中，尋找平均長度最短的區間，并將此預測區間定為最優預測區間。但是此類預測區間往往不存在，所以我們通常考慮將預測區間限制到同變預測區間里，以求得最優同變預測區間。

設樣本X=(X1，X2，…，Xn)，令δ1(X)=［l(X)，u(X)］是Y的置信水平為1-α的同等預測區間。若對任意實數c，有：δI(X+c)=［l(X+c)，u(X+c)］=［l(X)+c，u(X)+c］，則稱δI(X)是Y的位置同變預測區間。其中X+c=(X1+c，X2+c，…，Xn+c)。

設樣本X=(X1，X2，…，Xn)，(Xi＞0，i=1，2，…，n)，令δI(X)=［l(X)，u(X)］是Y的置信水平為1-α的同等預測區間。若對任意實數c＞0，都有δI(cX)=［l(cX)，u(cX)］=［cl(X)，cu(X)］，則稱δI(X)是Y的尺度同變預測區間。其中c(X)=(cX1，cX2，…，cXn)。

文獻［1］討論了位置分布族與尺度分布族中的分布參數含有序限制θ≤θ2(θ2未知)時，對未知隨機變量的最優同變點預測量進行改進;文獻［2］討論了位置分布族與尺度分布族中分布參數含有序限制θ≥θ1和θ1≤θ≤θ2(θ1，θ2未知)時，對未知隨機變量的最優同變點預測量進行改進。本文將利用未知參數的兩種序限制，即θ∈Θ1={θ|θ≥θ1}與θ∈Θ2={θ|θ≤θ2}，構造出精確度一致的預測區間，在只需評價置信度優良的情況下，借助IERD方法，運用置信概率差的積分表示法對位置分布族與尺度分布族中未知隨機變量的最優同變預測區間進行改進。

若函數K(x，y)對于任意的的x1≤x2，y1≤y2，都有成立，則稱函數K(x，y)為

1 位置同變預測區間的改進

設隨機變量(X，Y)服從密度函數為f(x-θ，y-θ)且依賴于未知參數θ的分布，參數空間Θ={θ|θ∈R}，X為可觀測隨機變量，Y為未知隨機變量。構造置信水平為1-α的最優同變預測區間為：δIc0(X)=［l(X)，u (X)］=［X+c0-d，X+c0+d］，其中c0和d由方程∫c0+dc0-dh(v)dv=1-α與h(c0+d)=h(c0-d)唯一確定［4］。

下面將利用θ的兩種序限制，即θ∈Θ1={θ|θ≥θ1}與θ∈Θ2={θ|θ≤θ2}，對同變預測區間δIc0進行改進，并在一定條件下構造改進后的預測區間。

改進過程中需要借助下述引理：

引理1 對任意給定的x與λ≥0，h(x-λ，y)與g(x，y)是正函數，且是y的非增函數，則對任意給定的正數c1＞0，c2＞0及y1＞y2，都有

1.1 θ∈Θ1={θ|θ≥θ1}

引入可觀測隨機變量X1，即(X1，X，Y)的密度函數形式為f(x1-θ1，x-θ，y-θ)。

設W=X1-X，V=Y-X，則(W，V)聯合密度函數形式為gl(w-λl，v)，其中λl=θ1-θ≤0，且gl(w，v)=設Y的同變預測區間為，則利用置信概率差的積分

定理1 設(ⅰ)Gl(w，v)是TP2;

(ⅱ)φl(w)為w的非降函數，

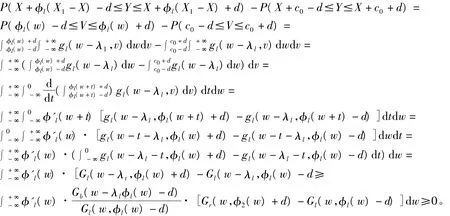
(引理1以及定理條件(ⅲ))

則P(Y∈δIφl)≥P(Y∈δIc0)，即δIφl(X)優于δIc0(X)。

1.2 θ∈Θ2={θ|θ≤θ2}

引入可觀測隨機變量X2，即(X，X2，Y)的密度函數形式為f(x-θ，x2-θ2，y-θ)，令U=X2-X，V=YX，則可知(U，V)的聯合密度函數形式為gr(u-λr，v)，其中設Y的同變預測區間為，則利用置信概率差的積分表示法可證明在一定條件下在下面的討論中，假設積分和求導運算可以換序。

定理2 設(ⅰ)Gr(u，v)是TP2;

(ⅱ)φr(u)為u的非降函數，

則對任意θ∈Θ2={θ|θ≤θ2}，有

0rr0

證明與定理1類似，故略。

2 尺度同變預測區間的改進

下面將利用θ的兩種序限制，即θ∈Θ1={θ|θ≥θ1}與θ∈Θ2={θ|θ≤θ2}，對同變預測區間δIc進行改進，并在一定條件下構造改進后的預測區間。

引理2 對任意給定的x與λ≥1， 是正函數， 是y的非增函數，則對任意給定的正數c1＞0，c2＞0及y1＜y2，都有下列不等式成立：

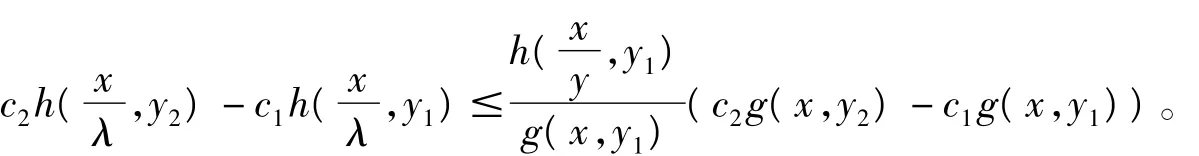
2.1 θ∈Θ1={θ|θ≥θ1＞0}

引入可觀測隨機變量X1(X1＞0)，即(X1，X，Y)的密度函數形式為則(W，V)的密度函數形式為根據尺度分布族的定義，可將

設Y的預測區間為作為評價預測區間優良性的標準之一，并可以此取代精確度。由于I(δIφl)=I(δIc)，則只需比較兩預測區間置信度即可。利用置信概率差的積分表示法可證明：在一定條件下，P(Y∈δIc)≤P(Y∈δIφl)，即δIφl優于δIc。在下面的討論中，假設積分和求導運算可以換序。

定理3 設(ⅰ)Gl(w，v)是TP2;

(ⅱ)φl(w)為w的非降函數

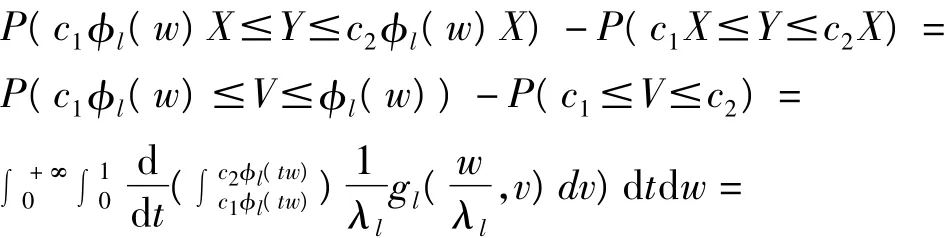
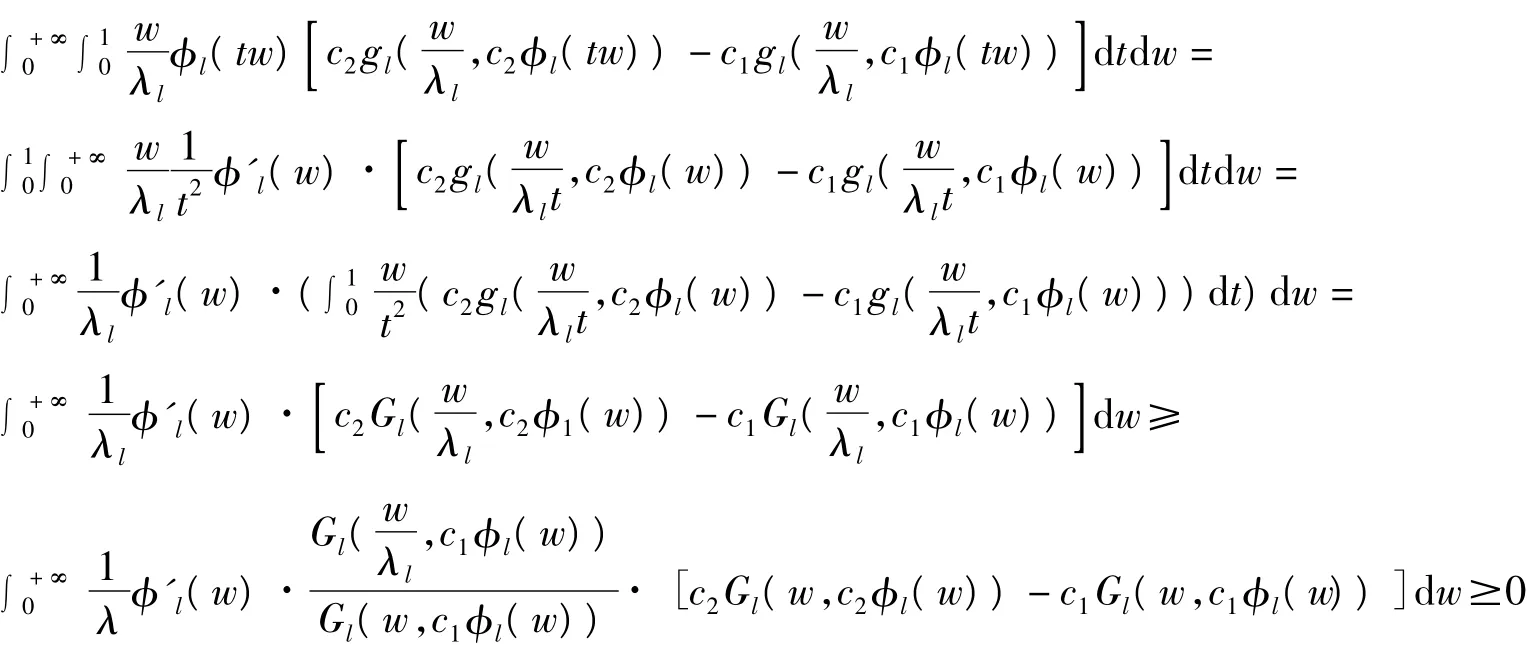
(由引理2以及定理條件(ⅲ))

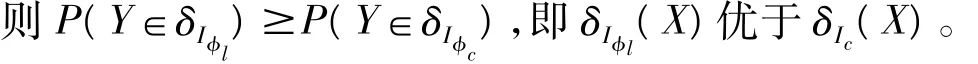
2.2 θ∈Θ2={θ|0＜θ≤θ2}

引入可觀測隨機變量X2(X2＞0)，即(X，X2，Y)的密度函數形式為則(U，V)的密度函數形式為令

定理4 設(ⅰ)Gr(u，v)是TP2;

(ⅱ)φr(u)為u的非降函數

證明與定理2.1類似，故略。

［1］ Xiao Yushan，Takada Y.Improvement of the best equivariant predictors under the ordered parameters［J］.Japan Statist.Soc，2006，36(1)：1-8.

［2］ Xiao YuShan，Takada Y.Statistical prediction under an order restriction.Northeast［J］.Math.J，2008，24(1)：1000-1778.

［3］ Karlin，S.Total Positivity［M］.Stanford CA：Stanforol University Press，1968.

［4］ Kubokawa，T.，Saleh，A.K.Estimation of location and scale parameters under order restriction［J］.Jour.Statistical Research，1994，28：45-51.

責任編輯：鐘 聲

The improvement of the best equivariant prediction interval under the ordered parameters

LIU Yan1，XIAO Yu-shan2
(1.Department of Fundamental Courses，Development College of Jilin Agricultural University，Changchun 130600，China; 2.Academic Affairs Office，Changchun University，Changchun 130022，China)

This paper considers the improvement of the best equivariant prediction interval under ordered unknown distribution parameters in the location or scale family.It constructs a class of improved prediction intervals under some conditions so that the problems of the unknown random variable have been solved by using the method of improving the best equivariant prediction.

order restriction;equivariant prediction interval;location family;sale family;TP2(total positivity of order 2);method of IERD(integrated expression of risk difference)

0212.5

A

1009-3907(2010)08-0014-04

2010-05-16

劉燕(1981-)，女，吉林長春人，助教，碩士，主要從事統計預測與決策理論以及貝葉斯分析理論的研究。