求解半定互補問題的一種非內點連續算法

楊曉麗，劉紅衛

(西安電子科技大學 理學院，陜西 西安 710071)

求解半定互補問題的一種非內點連續算法

楊曉麗，劉紅衛

(西安電子科技大學 理學院，陜西 西安 710071)

基于光滑FB函數理論和中心路徑原則，提出求解半定互補問題的一種非內點連續算法，在適當的條件下證得其全局線性收斂性和局部二次收斂性，并通過數值試驗驗證了算法可行性和有效性。

半定互補;非內點連續算法;光滑FB函數;全局線性收斂;局部二次收斂

0 引言

χ表示n×n對角實陣組成的空間，χ對矩陣加法X+Y，乘法XY，轉置XT，求逆X-1運算均封閉。χ的內積和范數：表示χ中的對稱矩陣組成的子空間，κ是S半正定陣組成的凸錐。所謂半定互補(SDCP)問題是：F是S→S的函數，尋找X∈S，使

1 光滑FB函數和中心路徑知識介紹

已知φμ：κ2→κ表示光滑的FB矩陣函數，μ＞0為光滑參數，I為n×n單位矩陣，

如果μ→0，那么

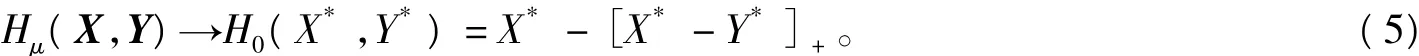
［X*-Y*］+是［X*-Y*］在κ上正交投影，H0(X*，Y*)=0?(X*，Y*)為(SDCP)(1)的解。

求解半定互補問題(SDCP)(1)思想：將之看成非光滑再生方程組H0(X，Y)=0，用光滑方程組Hμ(X，Y)=0逐步逼近它;在每次迭代中求一次光滑方程組Hμ(X，Y)=0，并通過逐步減小光滑參數μ，使μ→0，來達到‖Hμ(X，Y)‖減小的目地。然而實際中不可能得到方程組Hμ(X，Y)=0在μ＞0時的解。需引入(SDCP)(1)的中心路徑：

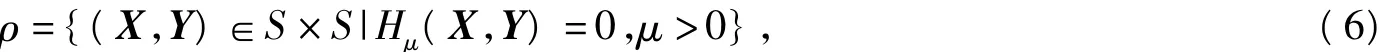
它的領域為

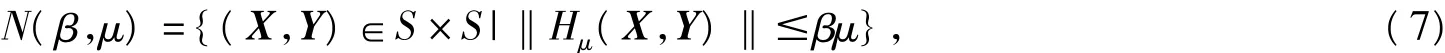
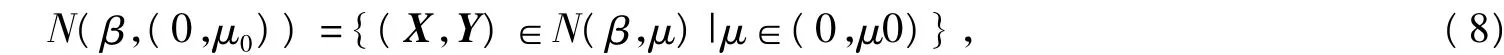
領域(7)一部分為

可求出Hμ(X，Y)=0一些近似解{X(μ)，Y(μ)}∈N(β，(0，μ0))。

φμ(X，Y)的性質：

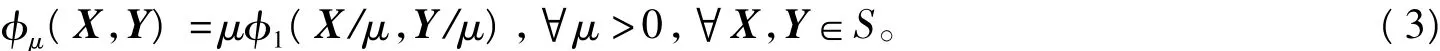
引理1［1］▽φμ是Lipschitz連續的。

再令

2 算法描述

算法1：Step0：選取δ，γ，σ∈(0，1)，任取(X0，Y0)∈S×S，μ0＞0，選β使

Step1：若μk=0，停止;(Xk，Yk)是(SDCP)(1)的一個解。否則，轉Step2。

Step2：若Hμk(Xk，Yk)=0，則令(Xk+1，Yk+1)=(Xk，Yk)，θk=1，轉Step4;否則，令(△Xk，△Yk)∈S×S為以下方程組的一個解

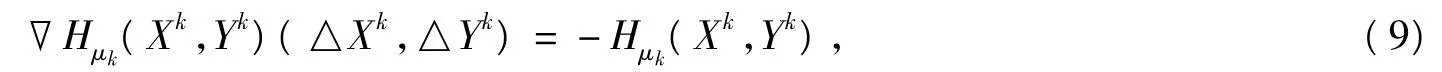
Step3：令θk=max{1，δ，δ}，并使

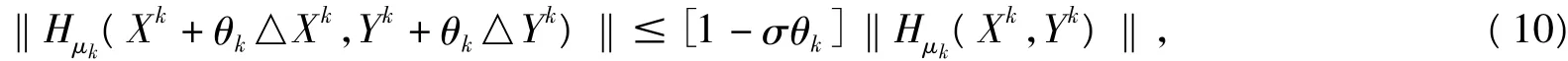
設定

Step4：令

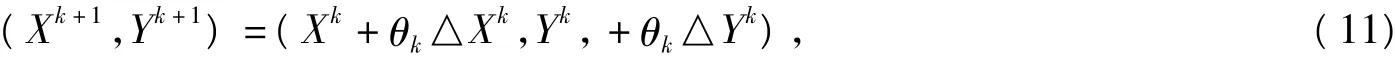
且ηk=max{1，γ，γ2，…}，使

(ii)理論上，把μk=0作為終止條件。然而實際中，經常把μk≤ε作為終止條件。

(iii)在算法第k次迭代中，若滿足條件‖Hμk(Xk，Yk)‖≠0，則需先解線性方程組(9)，再執行一次線搜索(10)即可;否則，算法不需要解方程組(9)和執行線搜索(10)。也就是說，在算法每次迭代中，至多需解一次線性方程組。

3 算法收斂性分析

假設A1 對任何β＞0和μ0＞0，(8)定義的領域N(β，(0，μ0))有界。

假設A2 對任何k≥0，0＜μk≤μ0，存在一常數ω＞0，使‖▽Hμk(Zk)-1‖≤ω。

假設A3 用Ω表示SDCP(1)的解集，對任何(X*，Y*)∈Ω，滿足條件X*+Y*＞0。

定理1 如果F是連續可微單調的，{(Zk，μk)}是算法產生的迭代序列，假設A1和A2均成立，▽F是Lipschitz連續的(k為Lipschitz連續常數)，那么存在一常數ρ∈(0，1)，

對所有的k，有μk+1≤ρμk。

證明：由(12)知，存在一個θ*∈(0，1］，對所有k，均有θk≥θ*。如果Hμk(Zk)=0，那么θk=1，以上結論顯然成立;另一方面，Hμk(Zk)≠0，由(9)和假設A2可知

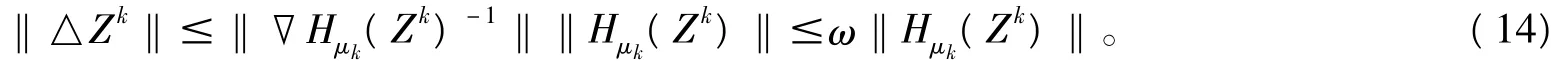
假設序列{0，1，2，…}存在一子序列K，當k→0時，有{θk}k∈K→0。考慮子序列K中的迭代，由(10)可得

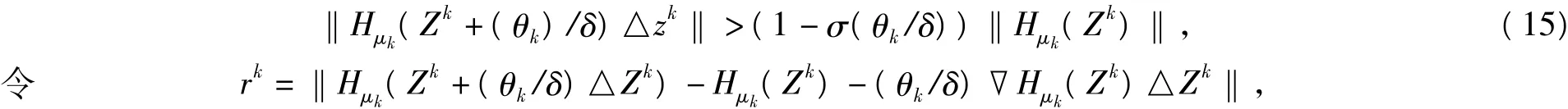
又由(10)可得

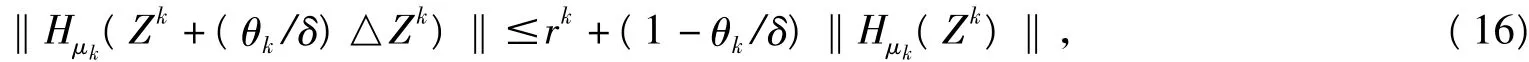
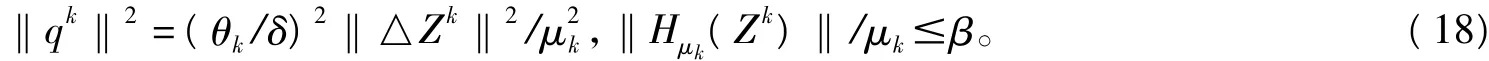
由引理1知▽φ1是Lipschitz連續的，設Lipschitz常數λ=2+8n，▽F也是Lipschitz連續的。那么由(3)，(14)和(18)，得到

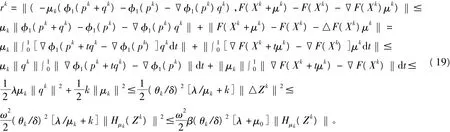
由(17)，(18)，(19)，得到

令(20)中k∈K，k→∞，已知θk→0，得到σ≥1，這與σ∈(0，1)矛盾。對所有k，有θk∈(0，1］，那么存在θ*∈(0，1］，對所有k，有θk≥θ*。由(12)知，對所有k，均有μk+1≤(1-σθk)μk≤(1-σθ*)μk，最后，令ρ= 1-σθ*，于是μk+1≤ρμk。定理得證。

以上定理1說明了算法的全局線性收斂性。下面定理2將說明其局部二次收斂性。

引理2 如果對任何(X*，Y*)∈Ω，假設A3均成立，那么X*-Y*可逆，▽φμ(X，Y)在任一點(X，Y)→(X*，Y*)是Lipschitz連續的。另外，對任何μ＞v≥0，存在一?＞0，

在任一點(X，Y)→(X*，Y*)，使

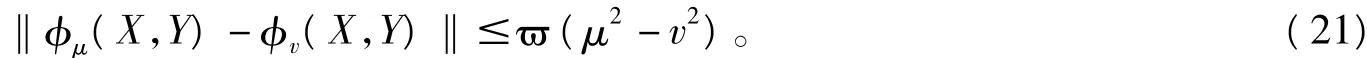
引理3 如果(i)F是單調連續可微的;(ii)(Z*，0)是算法迭代產生的序列{(Zk，μk)}的一個聚點; (iii)▽F是Lipschitz連續的;(iv)假設A1，A2，A3均成立;(v)存在一整數k0，對所有k＞k0，有Hμk(Zk)≠0。那么，存在一整數k∞＞k0，對所有的k＞k∞，有Zk+1=Zk+△Zk和μk=O(‖Zk-Z*‖)均成立［1］。

定理2 若引理3的(i)(ii)(iii)(iv)均滿足，則存在一kˉ，使μk+1=O()，?K=kˉ，kˉ+1，…。證明：不失一般性，假設{(Zk，μk)}收斂到(Z*，0)，那么存在一k^，對所有k＞k^，都有Zk∈N(Z*，ε)。令kˉ=max{k∞，k^}，于是，對任何k≥kˉ，考慮兩種情況：

如果Hμk(Zk)=0，那么根據引理2和算法定義，有=(1-σ)μk和

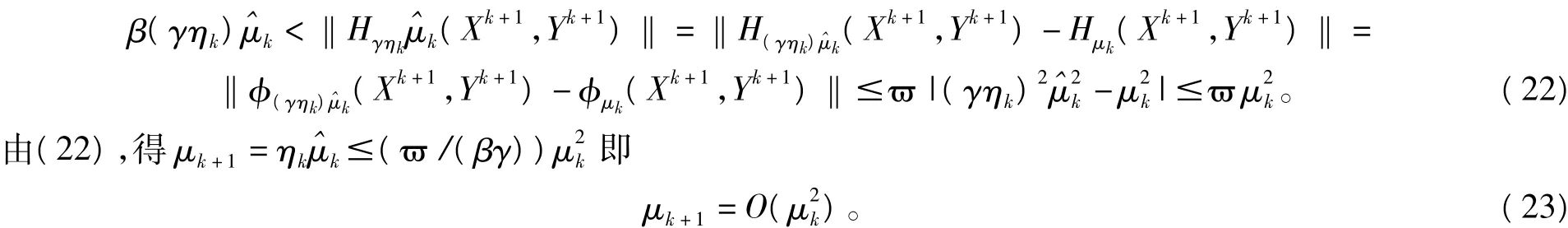
另一方面，如果Hμk(Zk)≠0，由假設A2，引理2和引理3，得

由A3，知道(X*-Y*)2＞0，因此它的特征值λ*i＞0，i=1，2，…，n。令Λ*=maxiλ*i，那

么存在一正交矩陣p，使

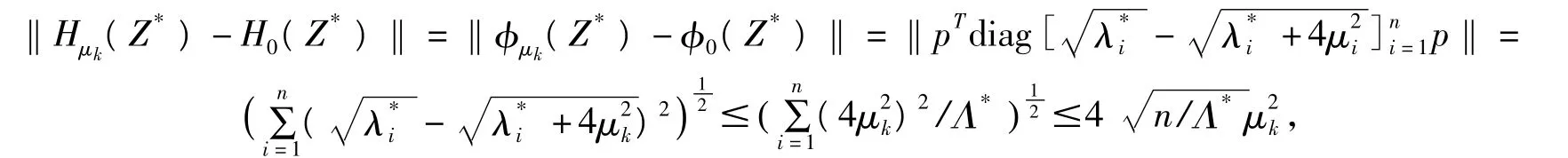
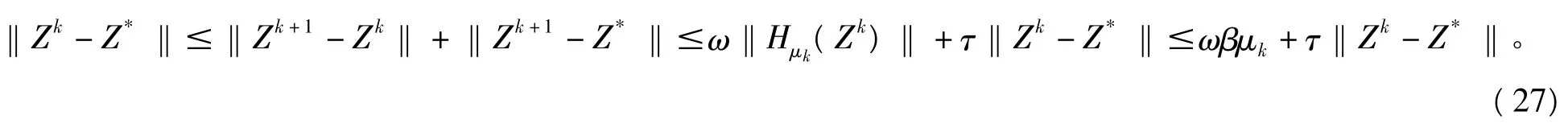
4 數值試驗

在試驗中，初始矩陣和參數值分別設為：X=3I，M=3I，Q=6I，Y=MX+Q，δ=0.5，γ=0.5，μ0=1，β=，允許誤差值ε=10-10，通過選取不同的σ，對n取不同值(即不同維數矩陣的情況)時，對算法1進行了試驗。試驗數據如表1所示：

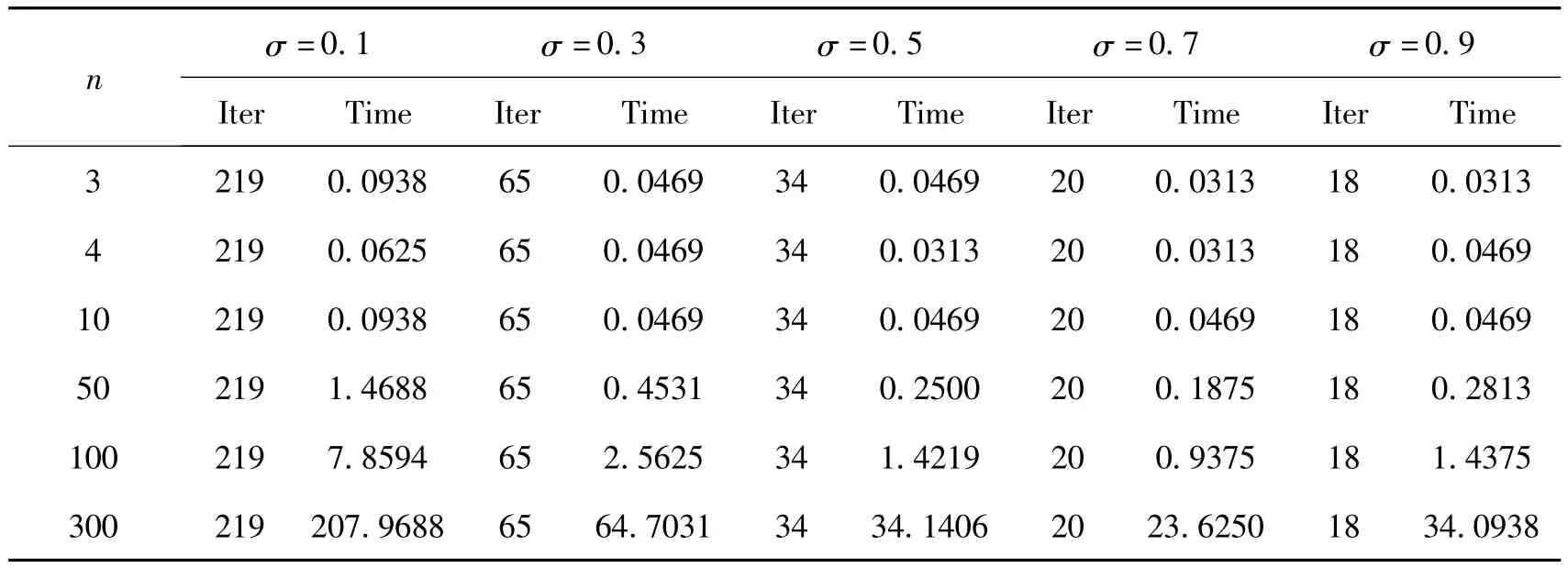
表1 算法1數值結果

以上表1，說明非內點連續算法1是求解半定互補問題的一種有效算法。

(i)從表1的列元素看，在σ取固定值，n取任何值時，數據有兩個明顯特征：一是算法的迭代次數都是固定的;二是算法運行時間幾乎是隨矩陣維數增加而變長。于是可以推得對于任何維的矩陣，算法1都是可行的、有效的。

(ii)從表1的行元素看，無論n取何值時，隨著參數σ的增長，算法的運行時間幾乎逐漸減短，迭代次數逐漸減少。于是可得出結論：參數σ值越大(不超過1)，非內點連續算法1越有效。

5結論

本文基于光滑的FB函數理論和中心路徑原則，提出了求解半定互補問題的一種非內點連續算法，數值試驗還說明了：參數σ的選取對算法的有效性有一定影響。

［1］ Chen，X.，Tseng P.Non-interior continuation methods for solving semidefinite complementarity problems［J］.Mathematical Programming，2003，95：431-474.

［2］ Burke，J.Xu，S.A non-interior predictor-corrector path following algorithm for the monotone linear complementarity problem［J］.Math program，2000，87：113-130.

［3］ Chen，B，Xiu，N.Superlinear noninterior one-step continuation method for monotone LCP in the absence of strict complementarity［J］.J.Optim. Theory Appl，2001，108：317-332.

［4］ 韓繼業，修乃華，戚厚鐸.非線性互補理論與算法［M］.上海：上海科學技術出版社，2006.

責任編輯：鐘 聲

A non-interior point continuation algorithm for solving semidefinite complementarity problem

YANG Xiao-li，LIU Hong-wei
(College of Science，Xidian University，Xi＇an 710071，China)

Based on the smoothing FB function theory and centre path principle，this paper gives a non-interior continuation algorithm for solving semidefinite complementarity problem and proves the global linear convergence and local quadratic convergence under some proper assumptions.Numerical experiments are made to show the feasibility and efficiency of the algorithm.

semidefinite complementarity;non-interior continuation algorithm;smoothing FB function;global linear convergence;local quadratic convergence

O224

A

1009-3907(2010)08-0006-04

2010-06-12

中央高校基本科研業務費專項資金資助［JY10000970004］

楊曉麗(1984-)，女，河北石家莊人，碩士研究生，主要從事最優化方法、半定規劃及其應用方面研究。