正弦電壓饋電的直線感應發射器加速特性

楊寶峰， 李耀華， 嚴陸光

(1.中國科學院 電工研究所，北京 100190;2中國科學院研究生院，北京 100049)

0 引言

直線感應發射器(linear induction launcher)的基本工作原理與傳統直線感應電機相同［1］，次級導體的感應電流在行波磁場的作用下產生電磁推力推動次級及其載荷沿發射器軸向運動。與傳統直線感應電機不同的是發射器的工作過程始終沒有進入穩態，電磁推力與速度一直處于動態變化過程中。建立直線感應發射器試驗平臺之前的必要準備工作之一便是預測其加速性能。

網孔矩陣法(mesh-matrix method)［2］或絲狀電流法(current filament method)［3］是分析線圈型電磁發射器的經典數值算法，其共同思想是將初級和次級沿垂直于軸線方向的平面進行環形剖分，每個剖分出來的圓環內電流沿周向均勻分布，通過計算圓環的自感，圓環間的互感、互感梯度、電磁力，從而得出線圈型電磁發射器的等效電參數和電磁推力。國際上幾家著名電磁發射研究機構根據這一思想，先后開發了自己的電磁發射仿真程序或軟件［2－6］。

基于正弦穩態電流的分析模型［7］為直線感應發射器的設計提供了理論參考基礎，但由于直線感應發射器一直處于瞬態運行模式，所以這種方法的預測結果與發射器特性會有很大的差距。鑒于直線感應發射器的主要饋電方式［8－12］，分析正弦電壓激勵的發射器特性則更具有代表性和普遍意義。本文以直線感應發射器的網孔矩陣方程為基礎，分析了三相正弦電壓觸發時序、幅值、頻率對直線感應發射器加速性能的影響。分析過程和結果為直線感應發射器的設計提供了理論參考。

1 直線感應發射器的物理模型與數值算法

1.1 基本結構與物理模型

直線感應發射器的基本幾何結構如圖1所示。發射器的初級由多個空心環型餅式線圈沿同一軸線排列構成;初級線圈內置套管，對初級線圈起保護作用，內膛作為次級的飛行軌道;次級為一般為圓柱型空心導體［4－5］。

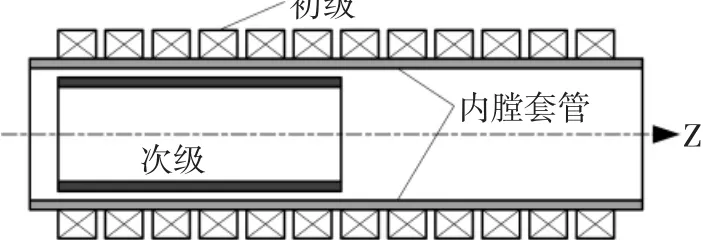
圖1 直線感應發射器的結構示意Fig.1 Construction of the linear induction launcher

基于網孔矩陣法的直線感應發射器集中參數電路等效模型如圖2所示。初級(驅動線圈，以字母d表示)和次級(彈丸線圈，以字母p表示)被沿垂直于軸線方向的平面進行環形剖分，每個剖分出來的圓環內電流沿周向均勻分布。實踐表明，忽略線圈的螺旋性和電流的不均勻性的分析方法應用于軸對稱線圈的磁場計算，不僅可以使計算工作量大為減輕，而且計算結果和實測數值之間僅有極小的誤差［13］。

根據網孔矩陣法，直線感應發射器的電路及運動特性方程為

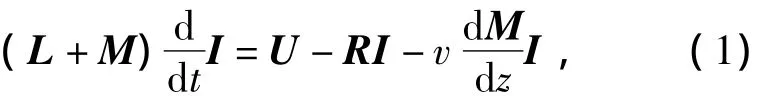
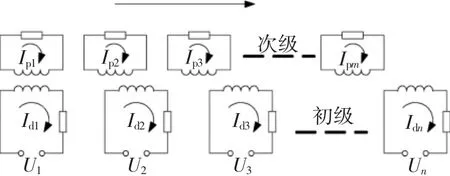
圖2 直線感應發射器的集中參數等效電路模型Fig.2 Equivalent lumped parameter circuit for linear induction launcher

式中:

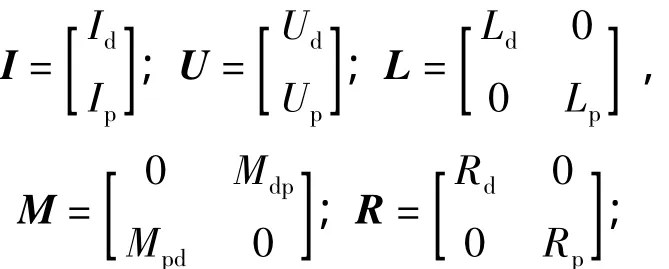
n和m表示線圈繞組的剖分單元數。I和U是兩種線圈的電流和電壓列矩陣，L和R是兩種線圈自感和電阻對角矩陣，M是兩種線圈互感方矩陣，dI/dt是電流對時間的變化率矩陣，dM/dt是兩中線圈互感對空間的變化率矩陣。mp是次級的質量，v是次級的速度，z是次級的位移。

當以三相正弦電壓激勵直線感應發射器時，特性方程中的電壓列向量矩陣為

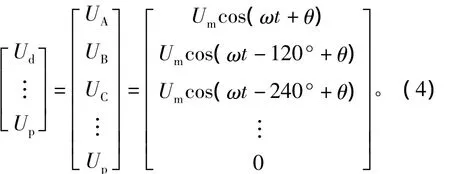
1.2 電感計算方法

直線感應發射器基于網孔矩陣法的集中參數電路等效模型計算的核心工作是每個剖分單元自感及任意兩個剖分單元之間互感的計算。

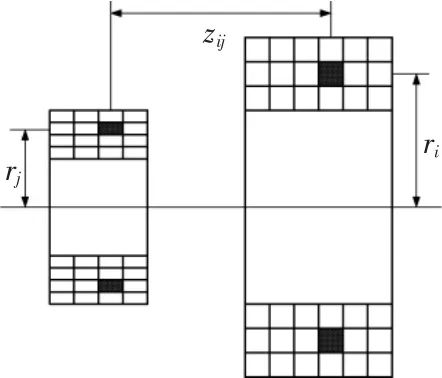
圖3 網孔矩陣法剖分線圈Fig.3 Subdivision arrangement of coils for mesh-matrix method

對兩同軸排列的耦合線圈進行如圖3所示的環形剖分，則兩個環形微元的互感

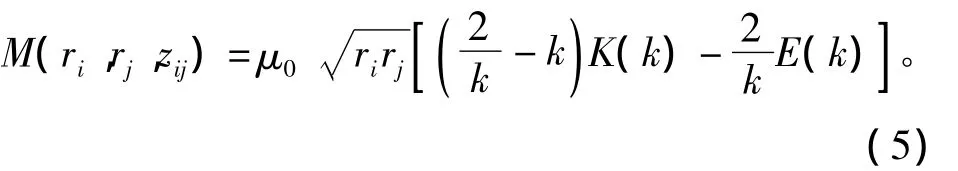
式中:ri和rj分別是兩線圈第i和j個基本微元的半徑;zij是這兩個基本微元的軸向中心距離;k與他們的關系為

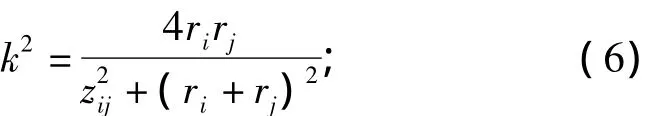
K(k)和E(k)分別是第一類和第二類完全橢圓積分，相應的表達式為

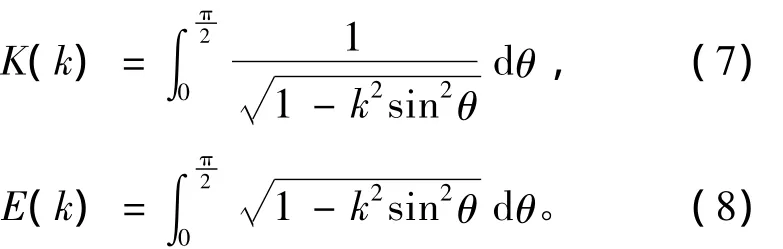
兩微元的互感梯度表達式可由式(5)導出，即

對所有微元的互感及互感梯度求和，得到兩線圈的互感及互感梯度

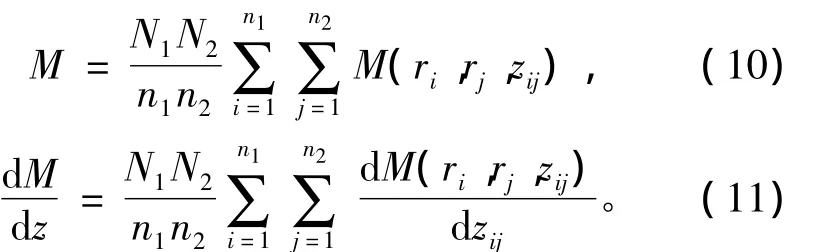
式中:N1和N2分別是兩個線圈繞組的匝數;n1和n2分別是兩個線圈的微元剖分數。

線圈的自感

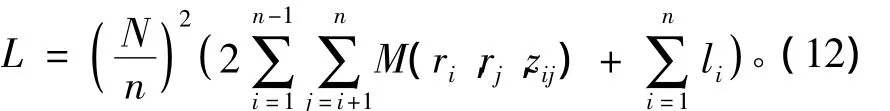
當剖分微元的橫截面為正方形時，li的計算式［14］

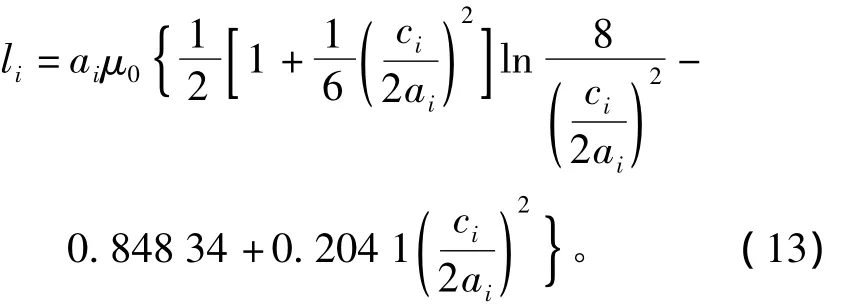
式中:μ0為真空磁導率;ci、ai分別為第i個剖分微元線圈的徑向厚度和平均半徑。

2 直線感應發射器在三相正弦電壓激勵下的加速特性分析

仿真所選直線感應發射器的初級由24個空心餅式線圈同軸排列構成，每個餅式線圈的軸向長度為0.04 m，初級軸向總長度為0.96 m，采用三相供電的方式，每相8個線圈。初級極距為0.12 m，極對數為4。每個餅式線圈的繞線匝數為60，線圈等效半徑為0.047 5 m。次級為圓柱型空心鋁筒，等效半徑為0.033，壁厚0.002 m，軸向長度0.24 m，質量0.274 8 kg，次級不攜帶其他負載。

2.1 電壓初始相位對發射器性能的影響

取電壓幅值Um=500 V，頻率f=500 Hz，ω=2πf，初始相位角θ=0。次級從左向右的運動方向為正方向，如圖1所示，次級左端面與初級左端面平齊的位置定為次級位移參考零點，則當次級初始位移為零時，初級繞組三相電流隨時間變化的曲線見圖4，為清晰起見，只給出了前5個周期的波形。

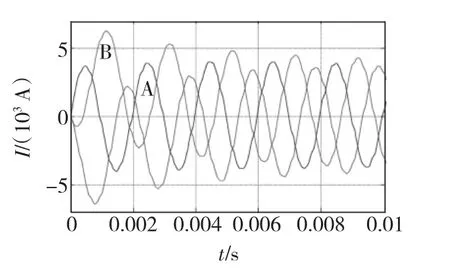
圖4 初級繞組電流Fig.4 primary currents

圖4中，三相電流不對稱，在通電的最初幾個電源周期內，B、C相電流有很大的直流分量。不對稱的三相電流，可能會對次級產生與運動方向相反的制動力。初始相位角θ=0時的電磁推力與時間的關系曲線如圖5所示。

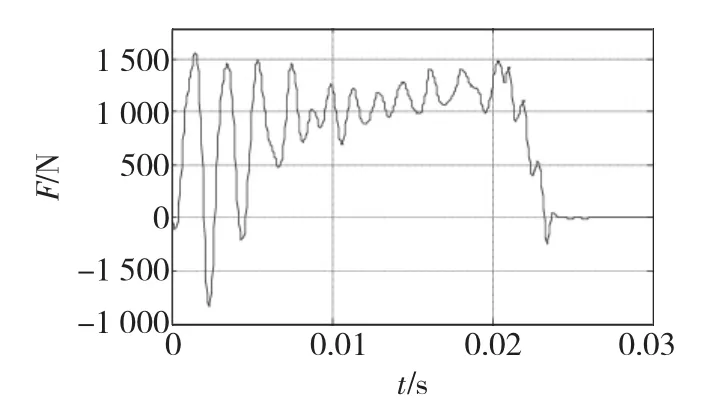
圖5 電磁推力與時間的關系(Um=500 V，f=500 Hz)Fig.5 Propelling force vs time(Um=500 V，f=500 Hz)

三相電壓的初始相位變化時，三相電流不對稱性也隨之變化，從而對發射器的加速過程產生不同的影響，導致次級的出膛速度的變化。次級出膛速度vm與三相電壓初始相位的關系見圖6。由圖可知，在相同的電壓作用下，存在使次級出膛速度最大的最佳電壓初始相位。對于不同規模的加速器，電壓初始相位對次級出膛速度的影響不同，對于選擇的仿真模型參數，電壓初始相位對次級出膛速度的影響并不明顯。

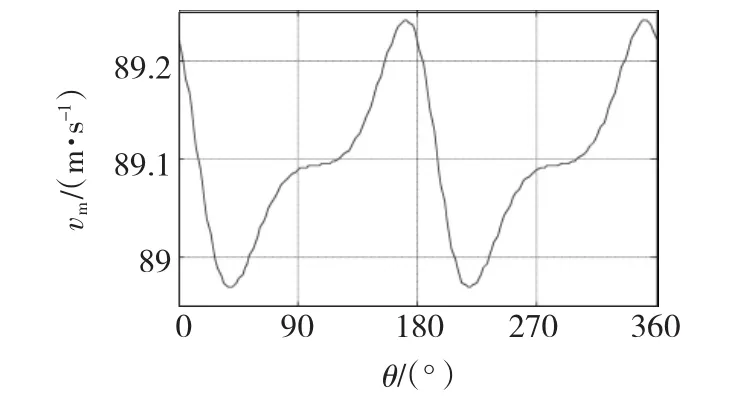
圖6 出膛速度與電壓相位角的關系Fig.6 Muzzle velocity vs phase angles

2.2 電壓幅值對發射器性能的影響

取三相交流電壓的頻率為f=500 Hz，次級出膛速度與電壓幅值的關系如圖7所示。電壓幅值小于600 V時，次級出膛速度隨電壓幅值的增大而提高;當電壓幅值大于600 V時，次級出膛速度隨電壓幅值提高的速度明顯變緩并出現波動，這是由于在次級即將出膛時，電磁推力迅速減小并出現負值，高電壓幅值可能會產生更大的制動力。在電壓幅值到750 V左右時，次級出膛速度已接近行波磁場的同步速度vs=120 m/s;電壓幅值，次級的出膛速度將在行波磁場同步速度值以下小范圍波動。如果希望次級出膛滑差控制在0.1～0.15，既出膛速度為102～108 m/s，則電壓幅值取值范圍為580～640 V。

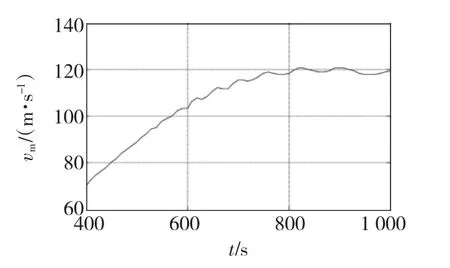
圖7 出膛速度與電壓幅值的關系(f=500 Hz)Fig.7 Muzzle velocity vs voltage amplitudes(f=500 Hz)

圖8示出了當電壓幅值分別為600 V和800 V時的電磁推力與時間的關系。由圖可見，電壓幅值為800 V時，電磁推力作用時間短，電磁推力最大值接近600 V時的兩倍，但次級出膛速度提高并不多。因此在次級出膛速度接近同步速度時，提高電壓幅值只是對繞組的絕緣提出更高的要求、電磁推力的沖擊值更高，而對提高次級出膛速度沒有貢獻。

2.3 電壓頻率對發射器性能的影響

取三相交流電壓的幅值為Um=500 V，次級出膛速度與電壓頻率的關系如圖9所示。當電壓頻率為430 Hz左右時，次級出膛速度達最大值96 m/s，此時的行波磁場同步速度vs=103 m/s，出膛滑差為0.068;當電壓頻率低于430 Hz時，次級出膛速度均比較接近于對應的行波磁場同步速度，不同的頻率時，次級出膛時的電磁推力波動情況不同，所以出膛速度隨電壓頻率值的增加而變化時的曲線并不十分光滑;當電壓頻率高于430 Hz時，次級出膛速度低于對應的行波磁場同步速度值較大，次級出膛時的電磁推力波動較小，出膛速度隨電壓頻率值的增加而變化時的曲線比較光滑。

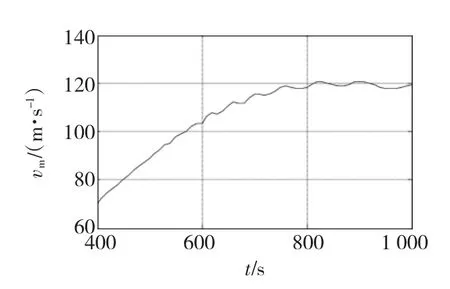
圖8 電磁推力與時間的關系(f=500 Hz)Fig.8 Propelling force vs time(f=500 Hz)

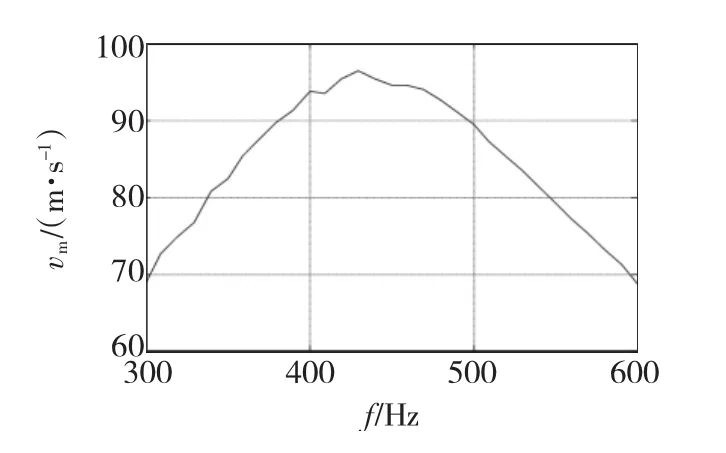
圖9 出膛速度與電壓頻率的關系(Um=500 V)Fig.9 Muzzle velocity vs voltage frequencies(Um=500 V)

圖10給出了電壓頻率為330 Hz、430 Hz、530 Hz時的電磁推力對時間的關系。電壓頻率為330 Hz時，電磁推力沖擊值較大，次級速度很快接近磁行波的同步速度，電磁推力值迅速減小，并在次級即將出膛前后出現正負波動;電壓頻率為430 Hz時，電磁推力的沖擊值小于330 Hz時的值，電磁推力作用時間長于330 Hz時的值，次級即將出膛前后電磁推力正負波動較小，次級出膛速度略小于磁行波的同步速度;電壓頻率為530 Hz時，電磁推力沖擊值最小，作用時間最長，次級出膛速度遠小于磁行波的同步速度。

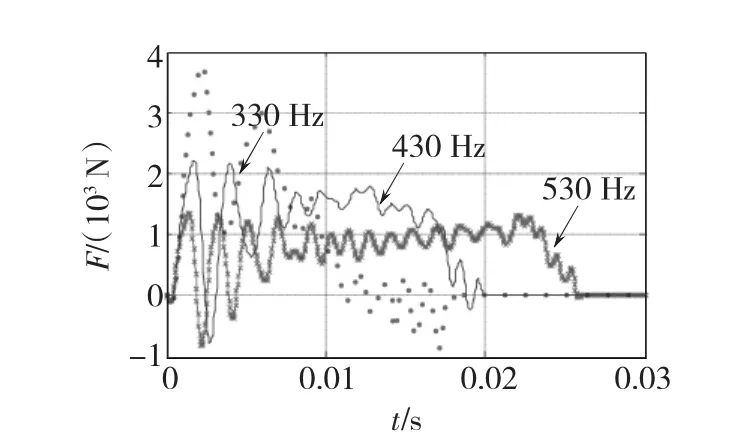
圖10 電磁推力與時間的關系(Um=500 V)Fig.10 Propelling force vs time(Um=500 V)

由以上分析知，為使次級出膛速度最大，對于一定的電壓幅值，有比較合理的電壓頻率值與之對應，過高和過低的電壓頻率都不利于發射器加速性能的充分發揮。

3 結語

本文討論了直線感應發射器在三相正弦電壓饋電方式下的加速特性。對于結構參數確定的直線感應發射器，為使次級獲得最高的出膛速度，存在最佳電壓初始相位;當電壓頻率給定時，應合理選擇電壓幅值，低電壓幅值時次級出膛速度遠低于對應的磁行波同步速度，過高的電壓幅值需要更高的繞組絕緣等級，無益于提高出膛速度;當電壓幅值給定時，存在最佳的頻率值，過高和過低的電壓頻率都不利于發射器加速性能的充分發揮。

［1］ZABAR Z，NAOT Y，BIRENBAUM L，et al.Design and power conditioning for the coil－gun［J］.IEEE Transactions on Magnetics，1989，25(1):627 －631.

［2］ELLIOTT D G.Mesh-matrix analysis method for electromagnetic launchers［J］.IEEE Transactions on Magnetics，1989，25(1):164－169.

［3］WU A Y.Parameter studies for traveling wave coaxial launchers［J］.IEEE Transactions on Magnetics，1991，27(1):617 －622.

［4］WIDNER M M.WARP 10:a numerical simulation model for the cylindrical reconnection launcher［J］.IEEE Transactions on Magnetics，1991，27(1):634－638.

［5］ANDREWS J A，DEVINE J R.Armature design for coaxial induction launchers［J］.IEEE Transactions on Magnetics，1991，27(1):639－643.

［6］MARDER B.A coilgun design primer［J］.IEEE Transactions on Magnetics，1993，29(1):701 －705.

［7］HE J L，LEVI E，ZABAR Z，et al.Equivalent circuits and parameters for induction-type electromagnetic launchers［J］.IEEE Transactions on Magnetics，1993，29(1):696 －700.

［8］HE Jianliang，LEVI Enrico，ZABAR Zivan，et al.Concerning the design of capacitively driven induction coil guns［J］.IEEE Transactions on Plasma Science，1989，17(3):429－438.

［9］ZABAR Z，LU X N，LEVI E，et al.Experimental results and performance analysis of a 500 m/s linear induction launcher(LIL)［J］.IEEE Transactions on Magnetics，1995，31(1):522 －527.

［10］LIAO M，ZABAR Z，LEVI E，et al.Analysis of generator-drive linear induction launchers［J］.IEEE Transactions on Magnetics，1997，33(1):184－189.

［11］LIAO M，ZABAR Z，CZARKOWSKI D，et al.On the design of a coilgun as a rapid-Fire grenade launcher［J］.IEEE Transactions on Magnetics，1999，35(1):148－153.

［12］BALIKCI A，ZABAR Z，CZARKOWSKI D，et al.Flywheel motor/generator set as an energy source for coil launchers［J］.IEEE Transactions on Magnetics，2001，37(1):280 －283.

［13］雷銀照.軸對稱線圈磁場計算［M］.北京:中國計量出版社，1991.

［14］GROVER Frederick W.Inductance Calculations［M］.New York:Dover Publications Inc，1946.