利用 Jacobi橢圓函數展開法求解特殊類型的方程

沈水金

(1.上海大學 理學院,上海 200444;2.紹興文理學院 數學系,浙江紹興 312000)

利用 Jacobi橢圓函數展開法求解特殊類型的方程

沈水金1,2

(1.上海大學 理學院,上海 200444;2.紹興文理學院 數學系,浙江紹興 312000)

利用未知函數的變換,將非線性演化方程轉換為以新未知函數及其偏導數為變元的多項式型的非線性偏微分方程,再應用 Jacobi橢圓函數展開法,求解 sine-Gordon方程和 Dodd-Bullough-M ikhailov方程的精確周期解,所得的周期解包含孤波解.該方法同樣適用于求解其他非線性演化方程.

非線性演化方程;Jacobi橢圓函數;精確周期解;孤波解

Abstract:By transformation of a dependent variable,a nonlinear evolution equation (NLEE) is converted into a nonlinear partial differential equation(NPDE)with apolynomial type of a new dependent variable and its partial derivatives.A Jacobi ellip tic function expansion method is p roposed to construct the exact periodic solutions of several nonlinear equations—sine-Gordon equation and Dodd-Bullough-Mikhailov equation.Periodic solutions obtained with this method include the solitary solutions and the shock wave solutions.Themethod can also be app lied to other nonlinear evolution equations.

Key words:nonlinear evolution equation;Jacobi ellip tic function;exact periodic solution;solitary solution

自 1834年 Russell第一次發現孤波現象、1967年 Gardner等利用反散射方法求得 KdV方程的孤波解之后,尋找非線性演化方程[1-2](nonlinear evolution equation,NLEE)的顯示解成為非線性領域中的熱門課題之一,尤其是尋找高維非線性演化方程的孤波解和類孤波解.為了獲取非線性演化方程更多的精確周期解,人們提出了許多種方法,如 Hirota雙線性算子、B?cklund變換、Darboux變換、Painlevé展開法等.近年來,劉適達等[3-4]提出的 Jacobi橢圓函數展開法在求解非線性演化方程中得到了廣泛應用.該方法不僅能求得非線性演化方程 (組)的精確周期解 (其中包含孤波解),并且通過對 Jacobi橢圓函數展開形式進行適當修改[5-6],得到更多的精確周期解.但無論如何,Jacobi橢圓函數展開法都需要通過對 Jacobi橢圓函數次數的平衡[7]來求得 n值.因此,對于方程中出現的類似 sin u,eu等無法直接通過次數的平衡來求 n值的特殊式子,必須要對其進行等價替換,從而滿足次數平衡的要求.本工作主要通過用未知函數的等價替換,將非線性演化方程替換為,以新未知函數及其偏導數為變元的多項式型[8]的非線性偏微分方程,再通過 Jacobi橢圓函數展開法求解精確周期解.

1 Jacobi橢圓函數展開法

考慮非線性波動方程

其行波解為

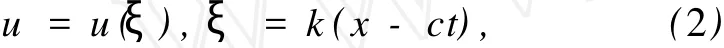
式中,k和 c分別為波數和波速.

將 u(ξ)展開為 Jacobi橢圓正弦函數 snξ的級數,有

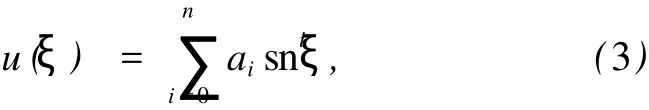
其最高階數為 O(u(ξ))=n.因為

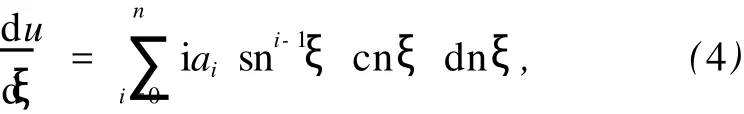
式中,cnξ和 dnξ分別為 Jacobi橢圓余弦函數和第三種 Jacobi橢圓函數,且具有如下性質:

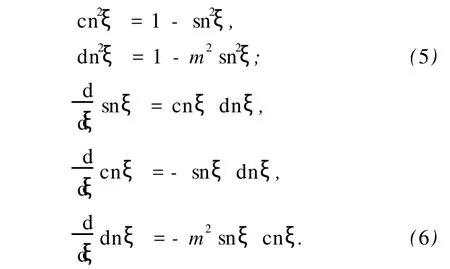
類似地,可以認為

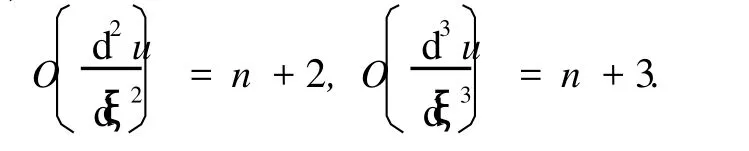
在式 (3)中選擇 n,使得非線性方程 (1)中的非線性項和最高階導數項平衡,從而求得方程的精確周期解.特別地,當 m → 1時,snξ=tanhξ,式 (3)就轉化為

所以,Jacobi橢圓函數法包含了雙曲正切函數展開法.

2 特殊方程的等價替換

Jacobi橢圓函數展開法需要通過對式 (1)中的非線性項和最高階導數項平衡來求式 (3)中的 n值.對于個別特殊類型方程中存在的類似 sin u,eu等的式子,無法直接通過平衡求解,因此,有必要對類似 sin u,eu等的式子進行等價替換.不妨作未知函數的替換:

顯然,若 v(x,t)是方程 (10)的解,則替換式 (7)所得到的 u(x,t)必定是方程 (9)的解,因此,方程 (9)與方程 (10)等價.

3 求解方程

3.1 sine-Gordon方程的精確周期解

由未知函數的替換公式 v=eiu,得

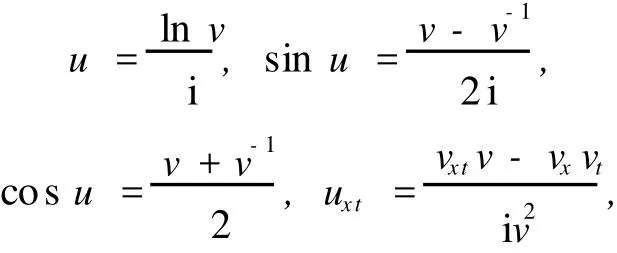
則方程 (9)與方程 (10)等價,因此,只需求方程 (10)的精確周期解.令

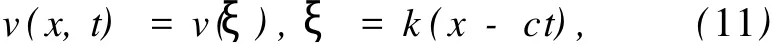
將式 (11)代入方程 (10),得

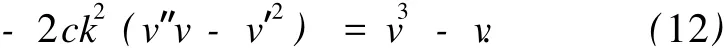
通過對最高階導數項和非線性項平衡,得 n=2,因此,可以假設方程 (12)有如下形式的解:

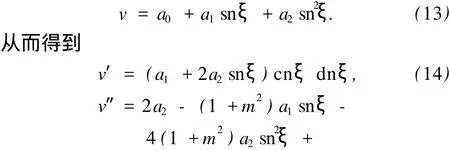
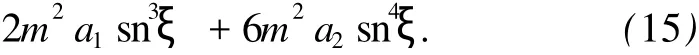
將式 (13)～(15)代入式 (12),得

通過吳消元法求得此方程組的解,情況如下.

情況1:

此時,方程 (12)的解為

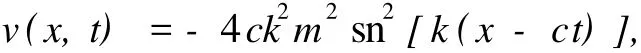
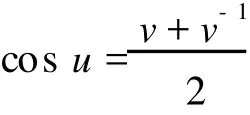
這就是 sine-Gordon方程的雙曲正切函數解,利用此解能求得該方程的孤波解.

情況2:

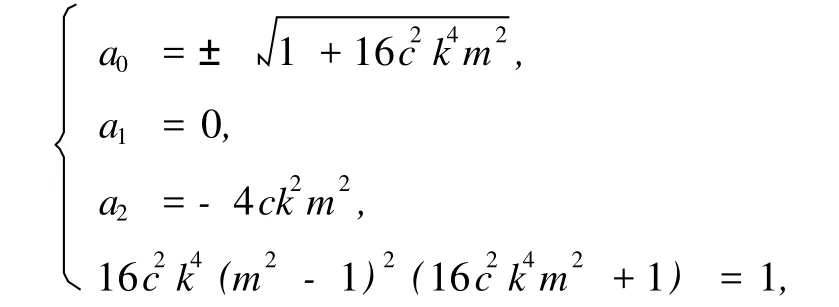
此時,方程 (12)的解為

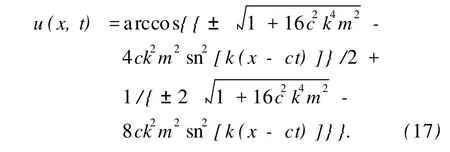
3.2 Dodd-Bullough-M ikha ilov方程的精確周期解

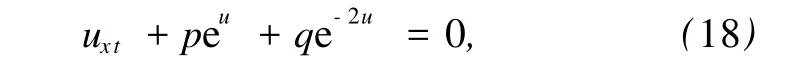
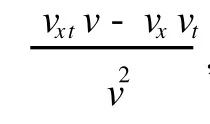
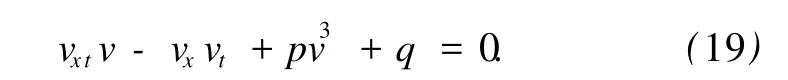
將式 (11)代入方程 (19),得

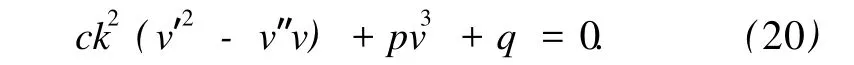
通過次數平衡,求得 n=2,因此,可以假設方程 (20)有如下形式的解:

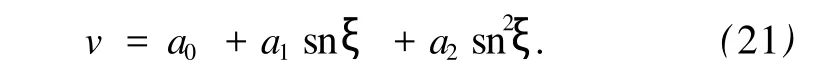
將式 (21)代入方程(20),令所得方程的各項系數為0,得

通過吳消元法,求得該方程組的解為

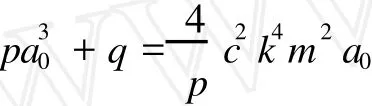
4 結 束 語

本工作利用 Jacobi橢圓函數展開法求解特殊類型的方程,關鍵在于利用未知函數的等價替換,將非線性演化方程轉變成為多項式形式的非線性偏微分方程.不同類型的未知函數需要不同類型的等價替換公式,從而得到非線性演化方程的精確周期解.最后指出,對于各種替換得到的等價方程,可以利用不同的求解方式來求得精確周期解.

致謝:衷心感謝導師夏鐵成教授的指導和幫助.

[1] 范恩貴.可積系統與計算機代數 [M].北京:科學出版社,2004:14-24.

[2] YANG L,ZHU Z G,WANG Y H.Exact solutions of nonlinear equation[J].Physics Letters A,1999,260(1/2):77-84.

[3] 劉式適,傅遵濤,劉適達,等.Jacobi橢圓函數展開法及其在求解非線性波動方程中的應用 [J].物理學報,2001,50(11):2068-2073.

[4] L IU SK,FU Z T,L IU SD,et al.Jacobi elliptic function expansion method and periodic wave solution of nonlinear wave equations[J].Physics Letters A,2001,289(1/2):69-74.

[5] ZHOU Y B,WANG M L,WANG Y M.Periodic wave solutions to a coupled KdV equations with variable coefficients[J].Physics Letters A,2007,308(1):31-36.

[6] 張善卿,李志斌.Jacobi橢圓函數展開法的新應用 [J].物理學報,2003,52(5):1066-1069.

[7] FAN E G. Extand tanh-function method and its app lications to nonlinear equations[J].Physics Letters A,2000,277(4/5):212-218.

[8] WU W T. Polynomial equation-solving and its application,algorithms and computation[M].Berlin:Sp ringer-Verlag,1994.

(編輯:孟慶勛)

Applications of Jacobi Elliptic Function Expansion M ethod to Several Special Nonlinear Equations

SHEN Shui-jin1,2
(1.College of Sciences,Shanghai University,Shanghai200444,China;2.Department of Mathematics,Shaoxing University,Shaoxing 312000,Zhejiang,China)

O 175.2

A

1007-2861(2010)04-0383-04

10.3969/j.issn.1007-2861.2010.04.011

2009-01-12

沈水金 (1980～),男,碩士,研究方向為計算數學.E-mail:zjssj595@yahoo.com.cn