分形的意義及應用
李雙雙,李 探
中國礦業大學信息與電氣工程學院,江蘇徐州 221116
1 分形的介紹
1.1 定義
分形(Fractal)是指具有自相似特性的現象、圖像或者物理過程等。分形學誕生于1970年代中期,屬于現代數學中的一個分支。分形一般有以下特質:
1)分形有無限精細的結構,即有任意小比例的細節;
2)分形從傳統的幾何觀點看如此不規則,以至于難以用傳統的幾何語言來描述;
3)分形有統計的或近似的自相似的形式;
4)分形的維數(可以有多種定義)大于其拓撲維數;
5)分形可以由簡單的方法定義,例如迭代。
1.2 來源
fractal一詞源于拉丁文形容詞fractus,對應的拉丁文動詞是frangere(“破碎”、“產生無規碎片”)。此外,與英文的fraction(“碎片”、“分數”)及fragment(“碎片”)具有相同的詞根。在70年代中期以前,曼德勃羅一直使用英文fractional一詞來表示他的分形思想。因此,取拉丁詞之頭,擷英文之尾的fractal,本意是不規則的、破碎的、分數的。曼德勃羅是想用此詞來描述自然界中傳統歐幾里德幾何學所不能描述的一大類復雜無規的幾何對象。例如,彎彎曲曲的海岸線、起伏不平的山脈,粗糙不堪的斷面,變幻無常的浮云,九曲回腸的河流,縱橫交錯的血管,令人眼花僚亂的滿天繁星等。它們的特點是,極不規則或極不光滑。直觀而粗略地說,這些對象都是分形。
1.3 分形的種類
逃逸時間系統:復迭代的收斂限界。例如:Mandelbrot集合、Julia集合、Burning Ship
分形迭代函數系統:這些形狀一般可以用簡單的幾何“替換”來實現。例如:康托集合、Koch雪花、謝爾賓斯基三角形、Peano曲線等等。
吸引子:點在迭代的作用下得到的結構。一般可以用微分方程確立。例如:Lorenz吸引子。
2 分形的意義
2.1 分形幾何的基本思想
1)客觀事物具有自相似的層次結構,局部與整體在形態、功能、信息、時間、空間等方面具有統計意義的相似性;
2)分數維是刻劃分形的特征量。
2.2 分形幾何與歐氏幾何的比較
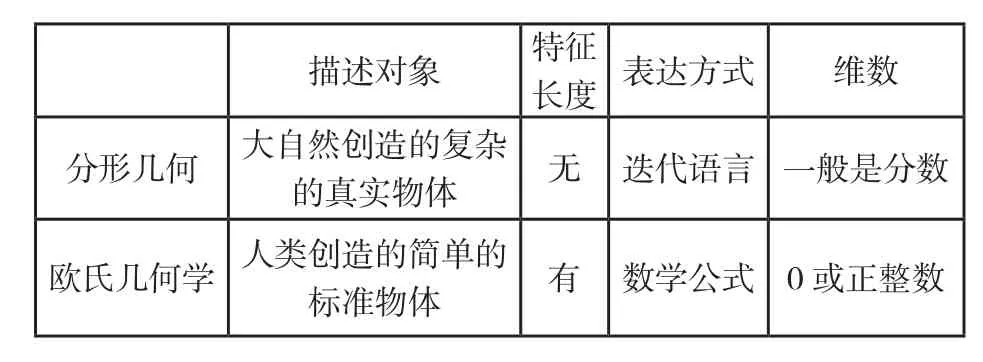
描述對象 特征長度 表達方式 維數分形幾何 大自然創造的復雜的真實物體 無 迭代語言 一般是分數歐氏幾何學 人類創造的簡單的標準物體 有 數學公式 0或正整數
3 分形的應用
3.1 運用分形的方法研究金融市場
分形的理論和方法是用來研究復雜事物的,是目前為止人類所能找到的最新的和最好的方法,也是相對簡單的方法。而金融市場是人類經濟領域最為復雜的市場,在分形的觀念出現之前,所有的方法因為線性的致命局限而從未達到市場的實質,人們只能在摸索中一步步探索市場的奧秘。分形的理論出現之后,人們終于可以向復雜事物的內部前進,可以更好地認識金融市場。
3.2 將分形應用與醫學
分形還能用于描述和預示不同生態系統的演化,有一些科學家認為分形幾何有助于他們理解被觀察的正常活細胞的結構和組成癌組織的病細胞的結構。所以通過建立與健康的或患病的組織相像的分形生長模型,科學家們也能夠了解存在于基因密碼的控制生長的信息,以及如果這種生長結果的信息被破壞時,癌組織是如何發展的。
3.3 研究分形建筑陶瓷紋樣、分形紡織紋樣設計及其印染工藝
長沙馬王堆漢墓出土的紡織品圖案紋樣很令人吃驚,圖案設計大膽豪邁、熱情奔放、生動流暢、不規則之中隱藏著高度的規則性、復雜的對稱代替了簡單的幾何對稱。這分明具有分形圖形的氣勢、風格。
3.4 設計分形時裝
現代西方時裝重色彩、質料而輕圖案裝點,而各國傳統民族服裝則正相反。對幾何紋樣的態度似乎是,西方重不規則、非對稱圖案,而各國傳統服裝重規則、對稱圖案(特別是伊斯蘭社會)。
4 結論
分形理論既是非線性科學的前沿和重要分支,又是一門新興的橫斷學科。作為一種方法論和認識論,其啟示是多方面的:一是分形整體與局部形態的相似,啟發人們通過認識部分來認識整體,從有限中認識無限;二是分形揭示了介于整體與部分、有序與無序、復雜與簡單之間的新形態、新秩序;三是分形從一特定層面揭示了世界普遍聯系和統一的圖景。它的應用將越來越廣泛。
[1]李水根.分形.北京:高等教育出版社,2004.
[2]譚芳.分形幾何的價值與研究.
[3]Mandelbrot.B.B,1982,The Fractal Geometry of Nature,San Francisco,Freeman.

