具有模糊搶修時間的震后道路搶修排程研究

霍建順，薛 梅，李愛慶

（西南交通大學 經(jīng)濟管理學院，成都 610031）

0 引言

強震對于交通網(wǎng)絡的影響非常巨大，會造成地面塌陷、龜裂，山體滑坡掩埋道路，橋梁的垮塌等等，這些都使得救援工作受阻。在5.12汶川地震中，多次由于道路受阻使得對汶川救援工作進展緩慢。由于地形復雜，強余震不斷、惡劣天氣、次生災害等，又使得道路搶修工作進行地極為艱難。再者震后應急期，緊急救援資源(營救設備、營救車輛、救護車和相關營救人員、通訊電力搶修人員等)通常都很有限，因而如何最有效地利用這些有限的資源，盡快地將道路搶通變得非常重要。實際中，應急階段對道路搶修的排程計劃通常根據(jù)決策者的經(jīng)驗進行安排，沒有考慮整個系統(tǒng)的目標，所做方案在理論上只是可行解，在實際運作時這些方案的實施效果可能會非常差。目前對震后道路災點的搶修排程問題，國內(nèi)外學者有了一定的研究。Cheng-Min Feng[1]將應急期界定為災后的72小時，并對高速公路的道路災點搶修排程進行了研究。Hitoshi FURUTA et al[2]則考慮了震后不確定性環(huán)境，如：余震，火災，天氣等因素，應用遺傳算法得到一個具有魯棒性的道路恢復排程的決策支持系統(tǒng)。Shangyao Yan et al[3,4]提出一種時空網(wǎng)絡模型來解決震后道路搶修排程的模型，并進一步地結(jié)合賑災物流情形進行討論。

本文考慮到強震后情況的復雜性，道路搶修不確定性很高，擬將道路災點的搶修時間設為三角模糊變量，使道路災點搶通時間滿足一定的置信度水平，并用機會約束規(guī)劃建構(gòu)數(shù)學模型，針對5.12地震后四川省什邡市的道路災點數(shù)據(jù)進行求解，并進行分析。

1 模型及算法

機會約束規(guī)劃是由Charnes和cooper提出的第二類隨機規(guī)劃，其顯著特點是約束條件至少以一定的置信水平成立。Baoding Liu et al[5,6]提出了模糊的機會約束規(guī)劃，并在文獻[7]中針對模糊決策系統(tǒng)構(gòu)建了minmax的機會約束模型。Yongshuang Zheng et al[8]針對旅行時間為模糊變量的車輛路徑問題構(gòu)建了一個機會約束規(guī)劃的模型，在有時間窗的情形下，最小化行駛距離，并設計了一種混合算法來求解此模糊車輛路徑問題。張建勇等[9]通過引入決策者主觀偏好值的概念，建立具有模糊特征的車輛路徑問題的模糊機會規(guī)劃模型，并設計了混合遺傳算法，在最小化總行駛距離的目標下進行了求解。

在強震應急期，政府交通主管部門根據(jù)收集到的道路受損情況，派出搶修工作隊進行道路搶修，對道路災點搶通的界定為至少有一條車道可通過即可。根據(jù)實際情況，本文對有關情形作如下假設：

（1）每個道路災點僅有一個工作隊進行搶修；

（2）各個工作隊的工作能力相同；

（3）在交通網(wǎng)絡中，工作隊的車輛優(yōu)先或?qū)Ｓ玫缆罚?/p>

（4）工作隊已掌握所有道路災點信息。

因為在震后應急期內(nèi)人民的生命依然受到直接威脅，為了盡快的開展救援工作，必須使得道路盡快搶通，因此在應急階段考慮的目標為最小搶修時間。在整個交通網(wǎng)路圖中，我們將有關符號進行如下說明：

i=0：工作站；

i=1,2,3,…,n：災點；

k=1,2,3,…,m：工作隊；

Lij：從災點i到j的旅行距離；

Tij：從點i出發(fā)至災點j的時間，由于旅行時間相對于維修時間非常小，故將旅行時間忽略。將Tij表示為從點i到點j的模糊維修時間；

[ai,bi]：維修 i點的時間窗，ai，bi分別為 i開始的時間和結(jié)束的時間。

我們用x，y和t三個決策變量刻畫運行計劃，其中：

x=(x1,x2,…,xn)：整數(shù)決策變量，表示n個不同的災點，對于所有的 i≠j，有 1≤xi≤n 和 xi≠xj，i,j=1,2,…,n。 實際上它是序列{x1,x2,…,xn}的一個重排。

y=(y1,y2,…,ym-1)：整數(shù)決策變量，y0≡0≤y1≤y2≤…≤ym-1。

t=(t1,t2,…,tm)：tk代表車輛k從工作站出發(fā)的時間，k=1,2,…,m。因工作隊投入搶修工作有序，其出發(fā)時間可能有差別。本文假定工作隊同時被指派，僅僅指派時間不全相同的情況，考慮在滿足道路搶修的時間窗下，各隊應在何時出發(fā)。

注意到運行計劃可以由x，y和t按下面的方式完全確定。對于每個k(1≤k≤m)，如果yk=yk-1，表示車輛k沒有運行；如果yk＞yk-1，則表示車輛k已運行，并且離開配送中心的時間為tk，它的行駛路線為

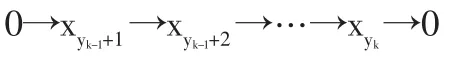
這種方法比較直觀，且只有n+2m-1個決策變量。另外，注意到以上定義的決策變量x，y和t保證了：（1）每個維修隊最多被派遣一次；（2）所有的路線都以工作站為出發(fā)和結(jié)束點；（3）每個災點有且僅有一個維修隊進行維修；（4）路線中沒有子圈。

設fi(x,y,t)為維修隊抵達災點i處的時間函數(shù)，它由決策向量x，y和t決定，i=1,2,…,n。由于當維修隊到達災點時候，應該立即進行維修，以爭取最短時間內(nèi)將道路搶通。如果維修隊 k 被派遣維修（即 yk＞yk-1），1≤k≤m，則對任何 2≤j≤ykyk-1，有

其中∧表示在兩者中取小（即搶修隊如果早到，立即投入搶修），由于Tij是模糊的，因此抵達時間 fi(x,y,t)，也是模糊變量，并且完全由上面兩式?jīng)Q定。

設g(x,y)是所有維修隊的旅行距離，有

其中

決策者根據(jù)實際情況給出災點i以置信水平βi在其指定的時間窗口[ai，bi]內(nèi)維修完成，于是 Cr{fi(x,y,t)∈[ai,bi]}≥βi,i=1,2,…,n。

可以應用痕跡檢驗方法檢驗油漆附著物，在發(fā)生多車碰撞交通事故的情況下，可以對同一部位印壓、刮擦痕上的油漆附著物進行檢驗，從而明確碰撞順序。具體而言，交通事故往往發(fā)生于瞬間，車輛相互作用力較大，車表面在外力的相互作用下容易出現(xiàn)破損、變形等情況。車輛表面往往會具有裝飾、保護功能的漆膜，因外力作用可能發(fā)生脫落、破損等狀況，遺落在其它相關車輛表面。基于此，當發(fā)生多車碰撞的事故時，以著力點為中心，進行痕跡檢驗，對油漆附著情況進行分析，即最上層所附著的油漆，為車輛最后碰撞所留，依次展開分析，有助于交通事故處理人員判斷車輛碰撞順序。

最后給出機會約束規(guī)劃模型

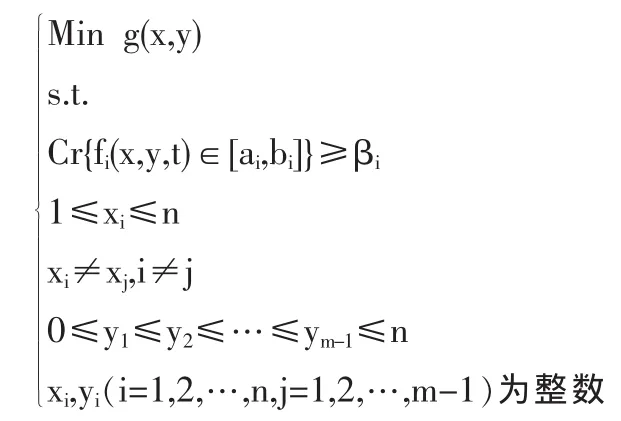
本文的利用隨機模擬和遺傳算法融合而成的混合智能算法進行求解，見Yongshuang Zheng[9]，劉保碇等[10]文中的算法描述。

2 案例

本文收集5.12汶川地震后四川省什邡市的有關數(shù)據(jù)，對什邡市的震后道路搶修排程問題進行研究。什邡市民政局提供的5.12汶川地震受災人口及其受災程度，如表1。

根據(jù)什邡市交通局提供的道路的受損情況，對道路災點進行整理如表2，其中連接重災區(qū)的道路災點以“*”表示。

由于什邡市的重災區(qū)很多，連接重災區(qū)的道路災點很多，假定工作隊每小時可搶修的受災路段長度為1km。搶修時間由前置災點的搶修時間加前置災點中最大的搶修時間表示。因震后道路搶修不確定性因素很多，本文將道路災點的搶修時間用三角模糊數(shù)表示，搶修時間列表略。

各災點由于連接的災區(qū)受損程度不同，因此在設定時間窗時，將結(jié)合災區(qū)情況予以考慮。本文將連接重災區(qū)的道路災點搶通須在60小時內(nèi)，連接一般災區(qū)的道路災點須在72小時內(nèi)搶通。將地震發(fā)生時點定義為0時，道路災點的搶修須在72小時內(nèi)完成，以便及時地對重災區(qū)民眾進行救助。各災點時間窗如表3。

在應急階段，道路搶修的目標是在最短時間內(nèi)搶通道路。因每個道路災點都需要搶修，因此道路災點搶修時間不再考慮，僅考慮旅行時間，旅行時間又依賴于旅行距離，所以將旅行時間最小化轉(zhuǎn)化為旅行距離最小化，各災點之間的距離見表4。

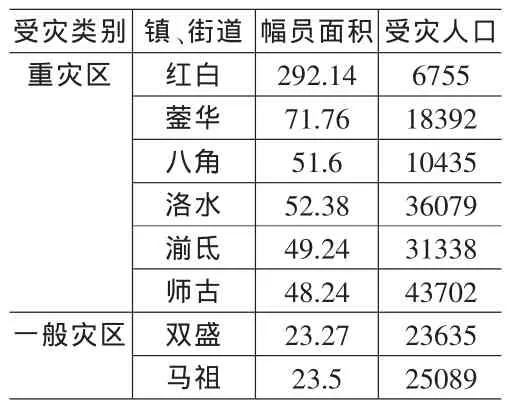
表1 什邡市“5.12”地震災害受災范圍表

表2 道路災點分布情況

續(xù)表

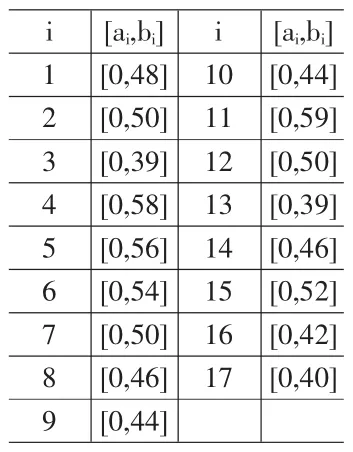
表3 時間窗

所有的工作隊從什邡市出發(fā)進行搶修，本文設定有4個工作隊，在0.9的置信水平下?lián)屝逓狞c。本文使用混合算法，用vc++6.0編程求解，其結(jié)果如下

工作隊1：什邡市→14→什邡市

工作隊 2： 什邡市→12→2→7→6→8→9→10→3→5→17→13→15→4→什邡市

工作隊3：什邡市→11→什邡市

工作隊4：什邡市→1→16→什邡市

此時的置信度為 Cr{fi(x，y，t)∈[ai，bi]，i=1，2， …，17}=0.985，四隊最遲分別于震后的4.9小時，3.0小時，1.2小時和3.1小時出發(fā)。從結(jié)果可以看出工作隊2承擔的工作量非常重，也說明在工作隊2的工作線路在滿足整個時間窗非常重要，這也符合什邡市交通網(wǎng)路“一縱兩橫”的特點，在實際中則需加強工作隊2的工作能力，如可以協(xié)調(diào)工作隊1，3，4協(xié)助工作隊2完成這條工作線路。

在變換工作隊數(shù)目時，在規(guī)定的時間內(nèi)完成的置信水平0.9的情況下，其置信度水平及總距離改變?nèi)绫?。

表4

表5

從表中可以看出，隨著工作隊數(shù)目的增加，在時間窗內(nèi)修通道路災點的置信水平是增加的，增加的幅度逐漸降低，但工作隊行駛的距離也是增加的，其與本文設置的M有關，使得工作隊在通過某些災點時其行駛距離有很大增加。

3 結(jié)論

地震應急期內(nèi)，對交通路網(wǎng)的搶修工作面臨的不確定性條件很多，在此種情況下，本文將搶修時間視為模糊變量，在總成本最小化的目標下，采用模糊約束規(guī)劃的方法構(gòu)建模型，并使用混合算法對問題進行了求解。

本文僅考慮一個災點僅被一個工作隊搶修的情況，實際中往往是會有多個工作隊搶修一個災點，將此假設條件放松，進而求解該問題是今后應繼續(xù)討論的。

[1]Cheng-Min Feng,Tsai-Chu Wang.Highway Emergency Rehabilitation Scheduling in Post-Earthquake 72 Hours[J].Journal of the Eastern Asia Society for Transportation Studies,2003,.5.

[2]Hitoshi Furuta,Ken Ishibashi,Koichiro Nakatsu,Shun Hotta.Optimal Restoration Scheduling of Damaged Networks Under Uncertain Environment by Using Improved Genetic Algorithm[J].Tsinghua Science And Technology,2008,13.

[3]Yan S.,Shih Y L.A Time-Space Network Model for Work Team Scheduling after a Major Disaster[J].Journal of the Chinese Institute of Engineers,2007,30.

[4]Shangyao Yan,Yu-Lin Shih.Optimal Scheduling of Emergency Roadway Repair and Subsequent Relief Distribution[J].Computers&Operations Research,2008.

[5]Baoding Liu,Kakuzo Iwamura.Chance Constrained Programming with Fuzzy Parameters[J].Fuzzy Sets and Systems,1998,94.

[6]Baoding Liu,Kakuzo Iwamura.A Note on Chance Constrained Programming with Fuzzy Coefficients[J].Fuzzy Sets and Systems,1998,100.

[7]Baoding Liu.Minimax Chance Constrained Programming Models for Fuzzy Decision Systems[J].Information Sciences,1998,112.

[8]Yongshuang Zheng,Baoding Liu.Fuzzy Vehicle Routing Model with Credibility Measure and Its Hybrid Intelligent Algorithm[J].Applied Mathematics and Computation，2006,176.

[9]張建勇,李軍.模糊車輛路徑問題的一種混合遺傳算法[J].管理工程學報,2005.

[10]劉保碇，趙瑞清，王綱.不確定規(guī)劃及應用[M].北京：清華大學出版社，2003.

[11]李軍，曾鸚，李妍峰.基于汶川地震的震后交通受損評估研究[J].管理評論，2008,(12).