運用遺傳算法對大學生體能教學訓練要素進行優化設計

金 萍，龍 駒2

（1.西華大學體育學院，四川 成都 610039；2.西華大學電氣信息學院，四川 成都 610039）

運用遺傳算法對大學生體能教學訓練要素進行優化設計

金 萍1，龍 駒22

（1.西華大學體育學院，四川 成都 610039；2.西華大學電氣信息學院，四川 成都 610039）

本文將排序自適應遺傳算法與單純形法相結合，設計了一種改進的、具有全局優化能力的混合遺傳算法，用該算法對大學生體能強弱（以心臟功能和肺功能作為主要考察依據）的教學訓練要素進行了優化設計，并在西華大學學生中進行了實驗研究。實驗結果表明，采用該法進行體能教學訓練比傳統方法具有更好的訓練效果，對提高大學生的體質健康具有創新意義。

遺傳算法；單純形法；大學生；體能；訓練要素

1 前 言

當前在大學生體能（以心臟功能和肺功能作為主要考察依據）教學訓練中，大都采用傳統的教學訓練方法，傳統方法雖能滿足基本的教學訓練要求，但在實踐中還缺乏一種優化的教學訓練模式，以進一步提高大學生的體能教學訓練效果。據此，我們采用了混合遺傳算法對大學生的體能教學訓練要素進行了優化設計，從而較快提高大學生體能教學訓練效果。

2 研究對象與方法

2.1 研究對象

運用遺傳算法對大學生體能教學訓練要素進行優化設計。其中選取西華大學2008級學生50人（男25人，女25人），年齡18～21歲，其中男生平均身高173.1厘米，體重60.6千克；女生平均身高159.9厘米，體重52.1千克。

2.2 研究方法

分別使用TJY-1高精度數顯電子臺階試驗測定儀和RCS-10000高精度數顯電子肺活量計對兩種模式教學訓練后學生的心肺功能進行了對比測試，獲取了相應的心肺功能數據。

3 應用遺傳算法設計體能教學訓練模式

大學生體能強弱（以心臟功能和肺功能作為主要考察依據）的教學訓練效果主要由運動量和運動強度兩個要素決定。本文針對這兩個要素用遺傳算法進行了優化設計，其具體的設計思路如下。

3.1 遺傳算法的算法設計

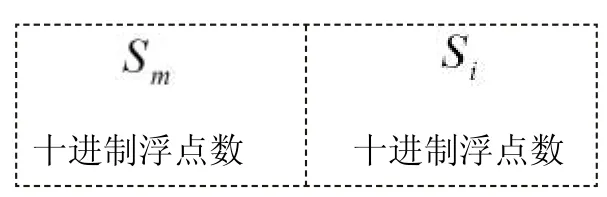
3.1.2 重要參數的選擇 遺傳算法要考慮的重要參數主要有：種群規模N（本設計中取N=100）、交叉概率和變異概率按照公式（2）進行設計。

3.1.3 適應度函數的設計 為了獲得滿意的動態特性，在引入懲罰功能的前提下，本文將目標函數取為

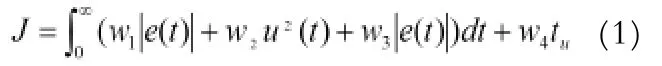
3.1.4 選擇運算設計 本文采用按照個體適應度大小排序的選擇方法設計相應的選擇算子。

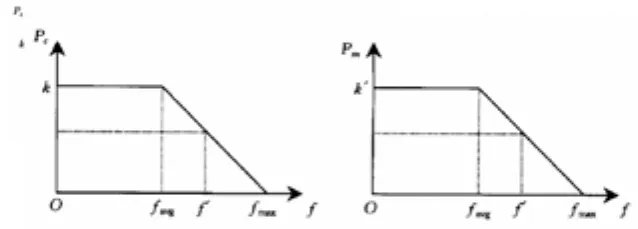
圖1 自適應交叉概率和變異概率示意圖

3.1.6 單純形局部搜索算法的設計 由于本文所設計的遺傳算法是遺傳算法與單純形法有機結合的一種混合算法,局部搜索能力很強的單純形法的加入執行過程如圖2中的流程圖所示。在加入單純形法的過程中主要考慮以下兩個方面的問題：（1）單純形搜索算法所需時間的分配問題：如果簡單地將遺傳算法和單純形法相結合，則整個算法的大部分運算時間將被單純形搜索算法所占據，而僅有很少的時間用于遺傳運算，這樣就不易體現出遺傳算法全局搜索能力強的優點；另外，單純形法搜索并不需要精確求解。因此，本文從兩個方面對單純形法搜索的時間加以限定，一是單純形法搜索迭代的次數 N ，在本文中經過多次實驗，限定對參與局部搜索的個體數加以限制），本文中經過多次實驗，單純形法參數的設置：反射系數,擴張

3.1.7 判斷算法終止條件是否滿足 用改進方法產生的初始種群通過混合遺傳運算后得到了新一代種群，將該代種群再次代入適應度函數進行檢測評估運算，觀察是否滿足算法終止條件，若滿足，則輸出最優解，尋優結束；若不滿足，則返回重復以上操作直到滿足為止。

3.2 應用遺傳算法進行優化設計的算法實現流程（圖2）

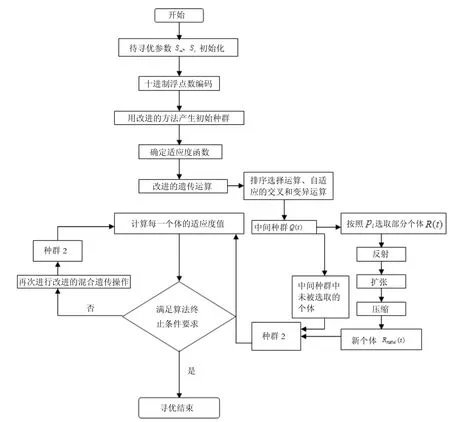
圖2 應用遺傳算法對學生體能教學訓練模式進行優化設計的算法流程

4 實驗結果

筆者分別使用心臟功能和肺功能測試儀對西華大學2008級學生（男25名，女25名）進行了兩種教學訓練模式（模式1為常規模式，模式2為遺傳算法模式）下臺階試驗和肺活量實驗指數的測定，其對比測試結果如表1、表2所示。

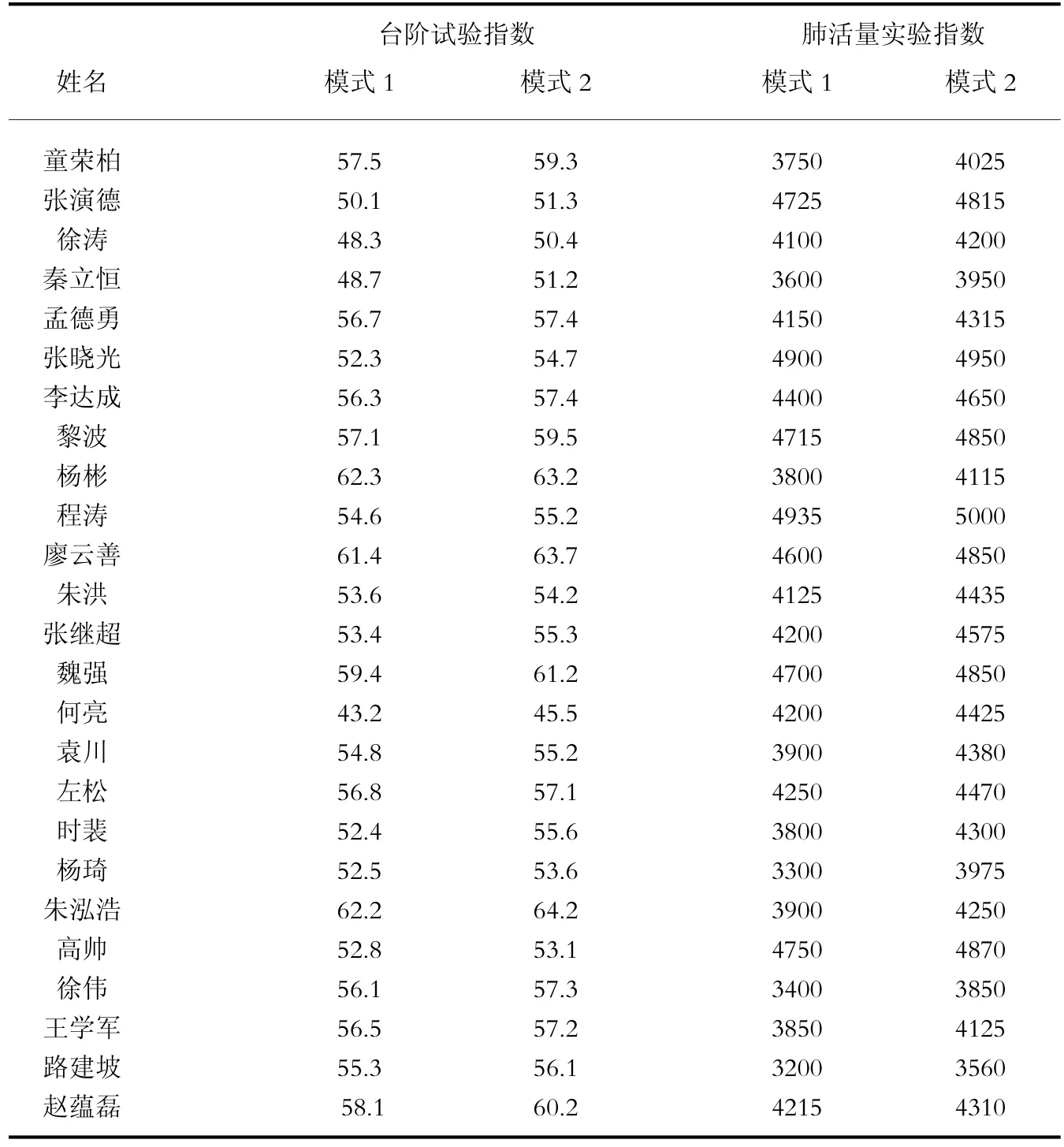
表1 男生實驗指數對比表

4.1 上述實驗結果表明，應用遺傳算法對大學生體能教學訓練要素進行設計后的教學訓練方法對大學生進行體能訓練，其訓練后的體能指標明顯優于傳統的教學訓練方法，從而說明了該方法對增強大學生的體能（心肺功能）具有明顯的效果，對提高大學生體質健康具有現實意義。

4.2 實驗結果還顯示，應用遺傳算法對大學生體能教學訓練要素進行優化設計后的方法對提高大學生的體能具有實用價值，是一種客觀、有效、快速的教學訓練方法，這種方法很容易推廣到其他體育教學訓練項目中，從而從新的視角提出了增強大學生體質健康的一種新的教學訓練模式。

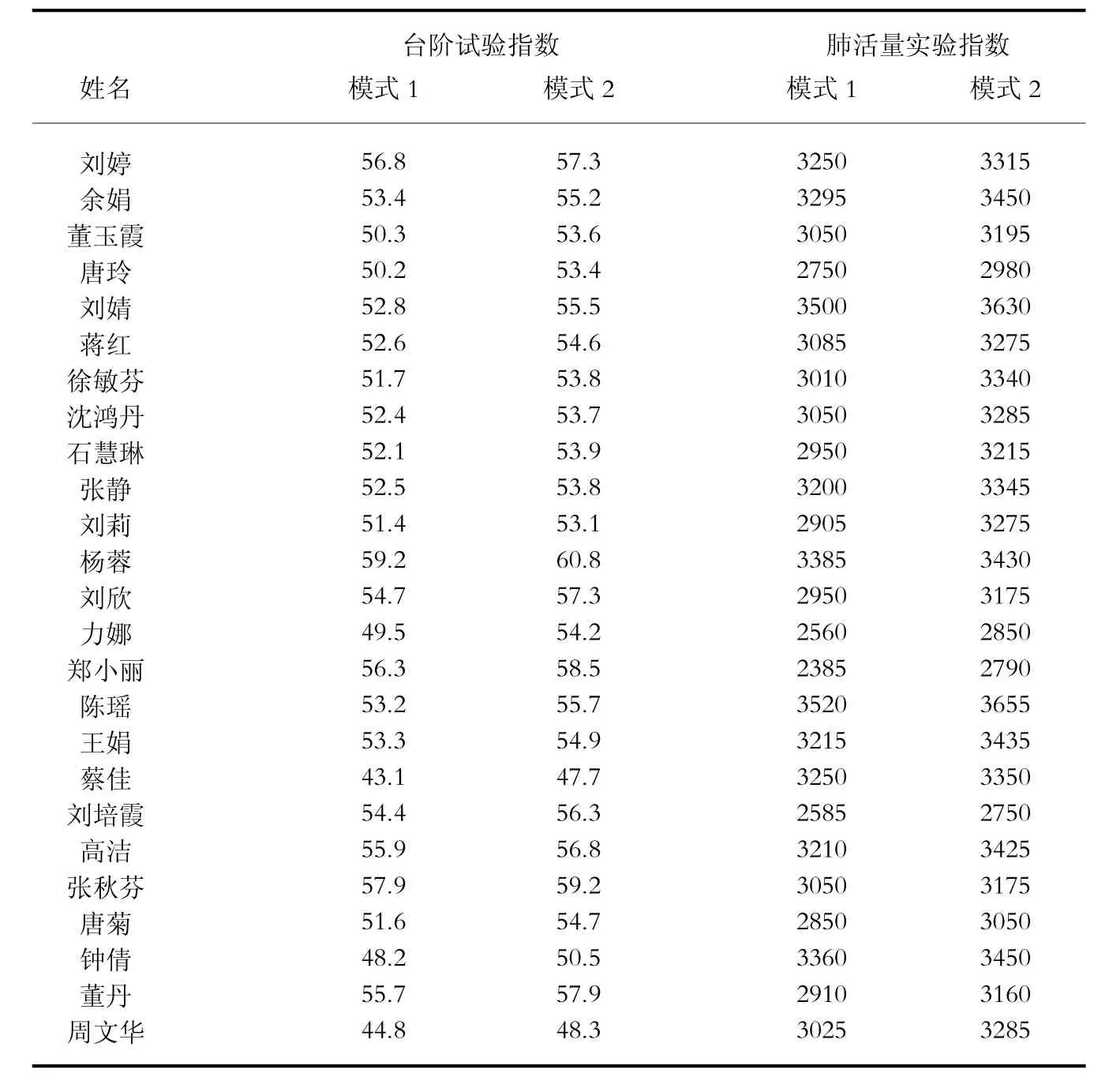
表2 女生實驗指數對比表

[1]周明，孫樹棟.遺傳算法原理及應用[M].北京：國防工業出版社，1999.

[2]牛志華.一類混合遺傳算法的研究[D].西安：西安交通大學，2002.

[3]王文平.遺傳算法：理論、應用與軟件實現[M].西安：西安交通大學出版社，2002.

[4]龍駒.永磁無刷直流電動機轉速控制系統的優化設計[M].成都：西南交通大學出版社，2006.

[5]Srinivas M, Patnaik L. M. Adaptive Probabilities of Crossover and Mutations in Gas. IEEE Trans. On SMC, 1994, 24（4）.

[6]陳德平.Kohonen神經網絡在體育運動聚類分析中的應用[J].體育科學，2005（3）.

G807.4

A

1674-151X（2010）10-104-03

10.3969/j.issn.1674-151x.2010.10.054

投稿日期：2010-07-29

金萍(1964 ～），副教授。研究方向：體育社會學。