軋機液壓壓下系統的特性分析＊

萬 巍,邱正明

(安徽工業大學工程實踐與創新教育中心,安徽馬鞍山 243002)

軋機液壓壓下系統的特性分析＊

萬 巍,邱正明

(安徽工業大學工程實踐與創新教育中心,安徽馬鞍山 243002)

通過建立液壓壓下系統位移控制方式下的數學模型,以及使用Matlab軟件對此方式下液壓壓下系統的動態特性進行了仿真,我們能夠確定:該系統是穩定的.從這可見系統建立的數學模型對液壓壓下系統的設計具有一定的參考價值.

液壓壓下;AGC;伺服閥;MATLAB仿真

液壓輥縫控制系統是提高板厚精度的重要技術措施.它的主要目標是在負荷狀態下動態消除因擾動引起的輥縫變化,減少鋼板在縱向上的厚度差,即同板差.由于現在的軋機自動化水平及對板帶材的質量要求越來越高,對液壓輥縫控制系統的控制要求也越來越高.而液壓壓下系統是液壓輥縫控制系統的主要執行機構,其動、靜態品質的好壞直接影響系統的穩定性、響應的快速性和控制精度.因此,對液壓壓下系統進行動態特性仿真的分析為以后優化這一系統,進一步提高板厚的控制精度有著重要的意義.

1 液壓壓下系統的工作原理

液壓壓下系統的方框圖如圖 1所示,液壓壓下裝置一般由位移傳感器、液壓缸和電液伺服閥等所組成.系統通過電液伺服閥對液壓缸的流量和壓力的調節來控制液壓缸上、下移動的行程來調節軋輥輥縫值.軋輥輥縫設定值經放大后輸出給電液伺服閥,驅動液壓缸動作,進行輥縫預設定.同時,液壓缸內的位移傳感器將實際軋輥位置信號反饋回來.當輥縫給定與反饋值相等時,液壓缸停止動作,輥縫調整完成.在軋制過程中,當軋制壓力發生變化時,其波動量由壓力傳感器測量出來,經位移轉換環節轉換成位移補償信號Δs.該信號再乘以調節系數,輸出給輸入環進行輥縫調節.當液壓缸的位移調整量達到Δs時,由位移傳感器反饋的信號與通過壓頭測量的補償信號相等.這時,調節完畢,由軋制壓力波動造成的軋機彈跳得到完全補償.

圖1 液壓壓下系統的方框圖

之后,轉換為大功率的液壓信號 (流量與壓力)輸出.公式為:

式中:Wsv—伺服閥的傳遞函數;

ωsv—伺服閥的頻寬,由樣本可得ωsv=194.78 rad/s;

ξsv—伺服閥的阻尼系數,參考樣本頻率響應曲線,計算出ξsv=0.258,則伺服閥的傳遞函數為:

動力元件的傳遞函數:

當以 Q0為輸入,Xp為輸出時,其傳遞函數為:

伺服放大環節的傳遞函數:

考慮到伺服放大器頻寬比伺服閥高得多,于是:

式中:Wa—伺服放大器的傳遞函數;

Ka—放大器 (PI D)的比例增益,取 Ka=0.146;

Gc(s)—校正環節的傳遞函數.位移傳感器:

由于系統中選用高精度、高響應的位置傳感器 ,因此:

式中:Wf—位移傳感器的傳遞函數;

Kf—檢測環節增益,取 Kf=100.

如圖 2所示.

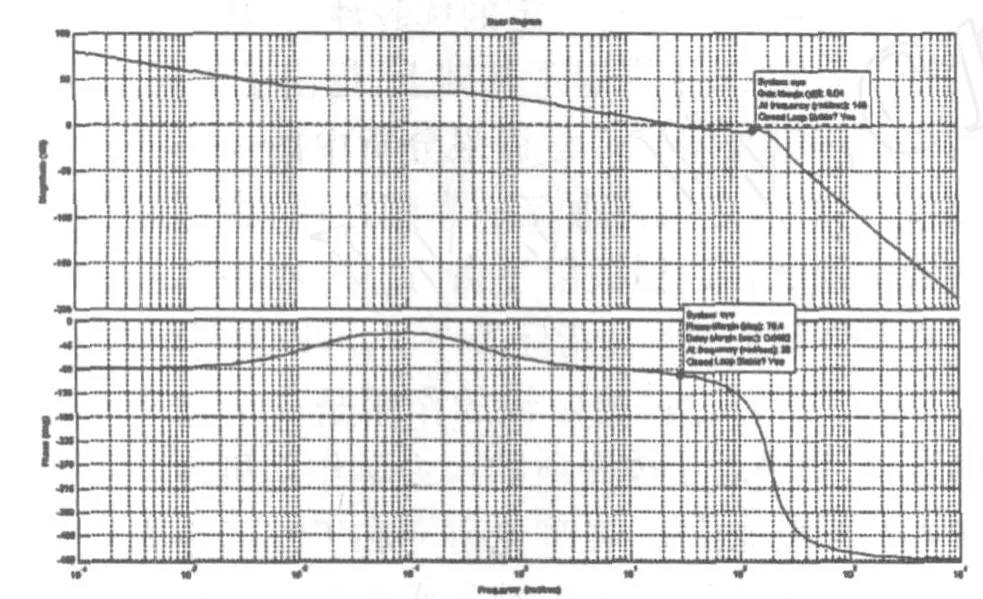
圖2 液壓壓下系統的 Bode圖

在 Simulink環境下,建立如下的系統模型:

圖3 液壓壓下系統的 Simulink仿真模型

對液壓壓下系統進行 matlab仿真,其單位階躍響應曲線如圖 4所示:

圖4 液壓壓下系統仿真結果

2 結論

由液壓壓下系統Bode圖可知,系統的幅值裕量Kg=6.04dB,相位裕量γ =79.4°,系統的幅值裕度大于 6 dB,相角裕度大于 60℃,說明此系統是穩定的,能滿足設計要求.

由液壓壓下系統單位階躍響應圖則可知系統的上升時間 tr=0.307s,最大超調量Mp=33.8%,調整時間(2%)ts=2.86s,調整時間 (5%)ts=2.06s,穩態誤差 ess=0,具有較好的時域響應特性.

[1]王春行.液壓控制系統 [M].北京:機械工業出版社,2001.

[2]黃忠霖.控制系統 MATLAB計算及仿真 [M].北京:國防工業出版社,2001.

[3]劉長年.液壓伺服系統優化設計理論[M].北京:冶金工業出版社,1989.

[4]肖志權,等.長行程閥控非對稱缸建模分析 [J].流體傳動與控制,2007,(1):19-22.

[5]王棟梁,等.非對稱閥控制非對稱缸的分析研究 [J].濟南大學學報,2003,(2):118-121.

TP271+.32

A

1008-4681(2010)02-0042-02

2010-01-04;

2010-02-10

萬巍 (1967-),男,湖南湘鄉人,安徽工業大學工程實踐與創新中心教師,工程師,碩士.研究方向:工程實踐教學與科研.

(責任編校:簡子)