LRC電路系統的對稱性與守恒量
錢華峰 王其申
(安慶師范學院數學與計算科學學院,安徽 安慶 246011)
LRC電路系統的對稱性與守恒量
錢華峰 王其申
(安慶師范學院數學與計算科學學院,安徽 安慶 246011)
Lagrange力學在類力學系統中有著重要的應用,利用Lagrange方程,可用來處理一些類力學系統的問題。本文運用Lagrange方程處理LRC電路系統,通過引入群的無限小變換,可以獲得該類力學系統的對稱性和守恒量。
類力學系統;LRC電路;對稱性;守恒量
Lagrange力學是分析力學的重要組成部分,但在很多非力學和非物理領域有著重要的應用,Lagrange方程的優點之一,可用來處理一些類力學系統的問題。本文運用Lagrange方程來處理由電感L,電阻R,電容C和電動勢E所組成的電路系統的問題。在LRC電路系統中,通過引入群的無限小變換,可以獲得該類類力學系統的對稱性和守恒量。
1 預備知識
我們首先分析最簡單的LRC串聯電路,如圖1所示

圖1
這是一個最基本的振蕩電路,如果電源是電動勢E=E0ejωt的穩態振蕩,則由電路中各元件的物理性質和歐姆定律,電路中的電流所滿足的方程是
這一方程與圖2所示的力學振動系統的振動微分方程

有著完全相同的形式。
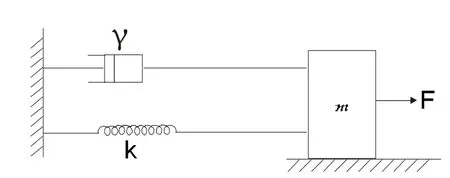
圖2
比較以上兩式,可以看到存在以下類比關系:

機械振動 質點位移(x) 質量(m) 彈簧常數(K) 阻尼系數(γ) 強迫力(F)電磁振蕩 電容帶電量(q) 自感系數(L) 電容量的倒數(C-1) 電阻(R) 電動勢(E)
根據這一對應關系,進一步可以指出兩個系統之間存在如下的能量之間的對應關系:

動能 勢能 耗散能 補充能源機械振動 1 2mx˙2 1 2kx2 1 2 γx˙ 2 F電磁振蕩 1 2Lq˙2 1 2cq2 1 2Lq˙2 E
此表說明:LRC電路中磁場能量相應于動能,電場能量相應于勢能,電阻耗損的能量相應于阻尼力所耗損的能量。
2 LRC電路系統的Lagrange方程
假設LRC電路系統由m個回路組成,每個回路由導線和電容,電感組成。用ik(k=1,2,…m)表示第k個回路中的電流,qk表示電容器中的電荷,它與電流之間的關系為q˙k=ik,Rk和Ck,Lk分別表示為第k個回路中的電阻和電容,電感。系統受理想,完整的約束,取qk為廣義坐標,LRC電路系統如圖3所示:
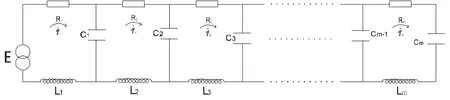
圖3
系統的Lagrange函數為:

系統的能量耗散函數為:
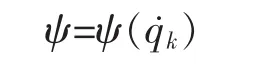
則系統的Lagrange方程為:
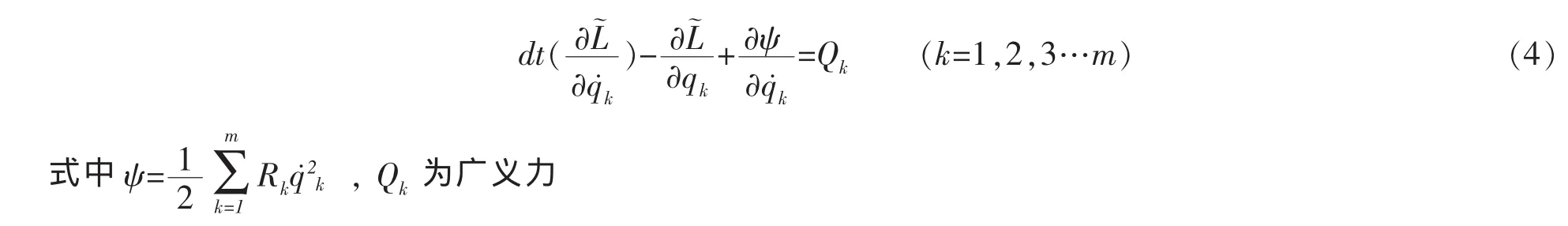
T,V分別為系統的動能和勢能
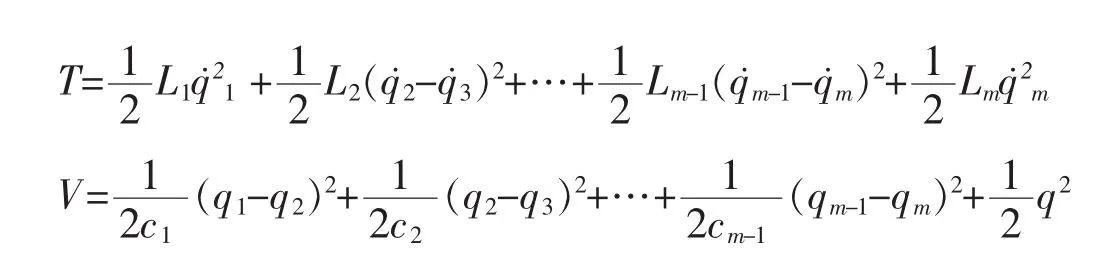
假設方程(4)非奇異,由(4)可解得:

3 LRC電路系統的Noether對稱性與守恒量
引進群的無限小變換:
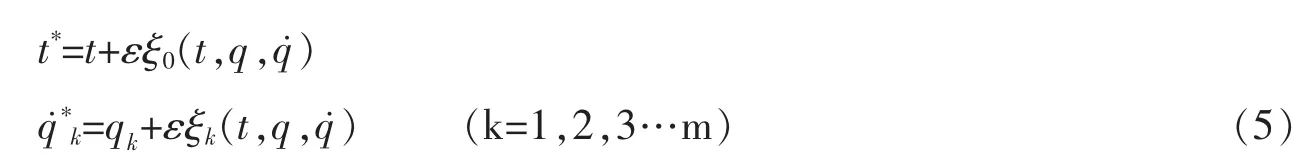
其中ε為無限小參數,ξ0,ξk為無限小變換的生成元或生成函數。取無限小生成元向量

式中右式為第二項對重復指標從1到m求和(下同)。其一次擴展為

以及二次擴展為
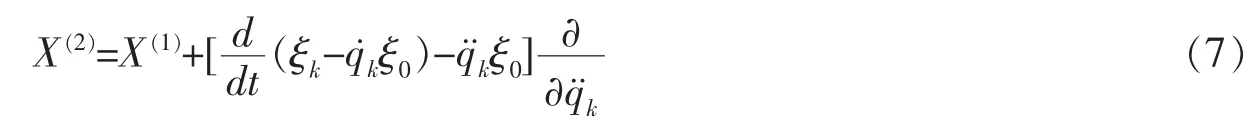
若LRC電路系統在變換(5)下,使Noether等式成立
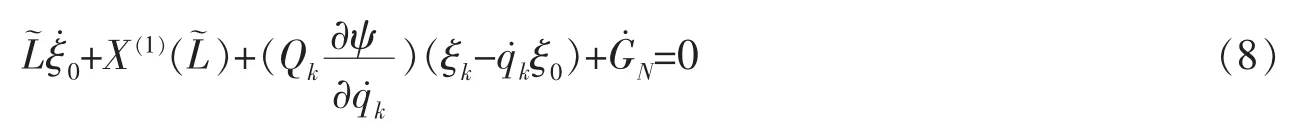
其中 GN=GN(t,q,q˙)稱為規范函數,則系統具有 Noether對稱性,并存在 Noether守恒量
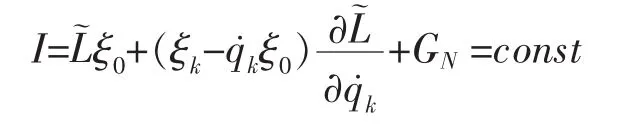
證明:
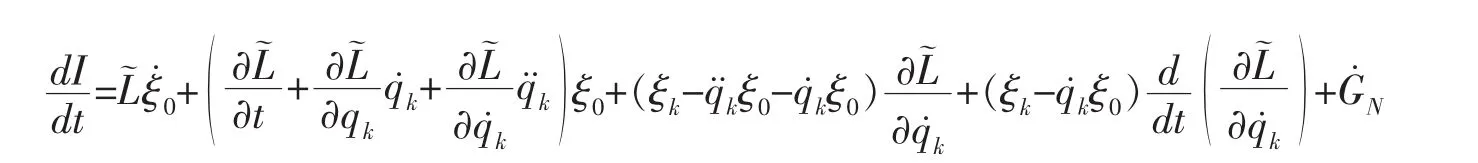
將(8)式中的 代入得:

將(4)代入上式得:
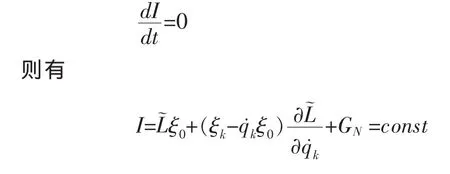
4 LRC電路系統的Lie對稱性與守恒量
方程(2)在無限小變換(5)下,Lie對稱性確定方程為:

利用(6),(7),(8)式得到

此方程為關于無限小生成元ξ0,ξk相對于LRC電路系統的確定方程。
對于滿足方程(9)的 ξ0, ξk如果存在滿足
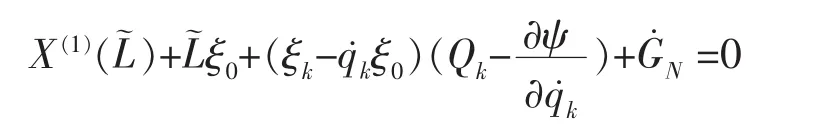
的函數 GN=GN(t,q,q˙),則存在對應于 Lie 對稱性的守恒量
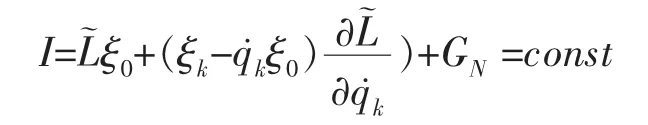
證明見(3)中的證明。
5 LRC電路系統的Mei對稱性與守恒量
假設在無限小變換(5)下,取無限小生成元向量
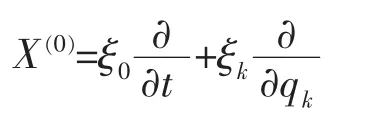
X(1)是無限小生成元向量X(0)的一次擴展,有
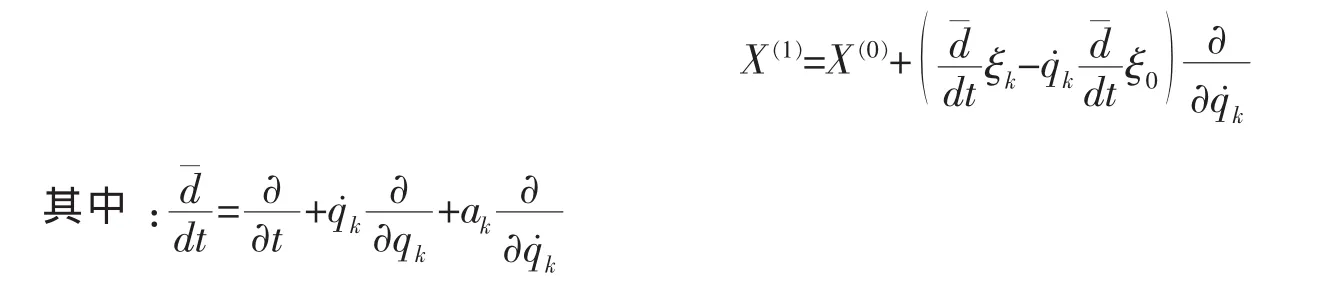
對LRC電路系統,生成元滿足如下方程
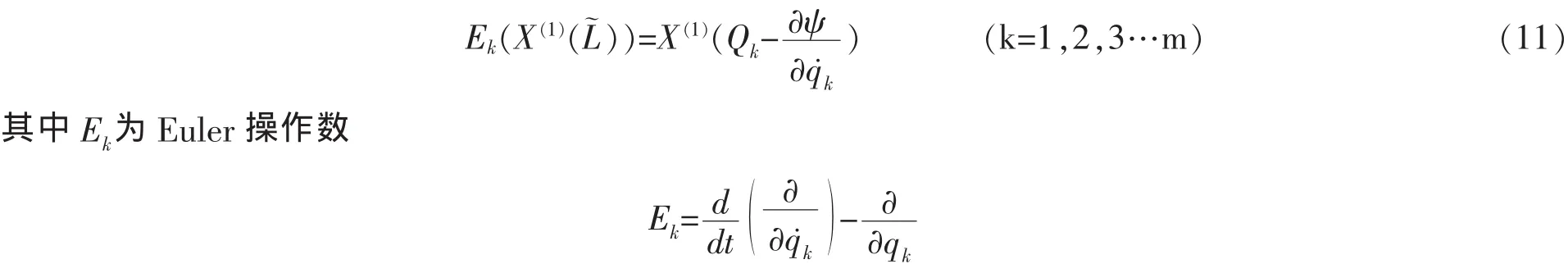
則相應的對稱性為LRC電路系統的Mei對稱性。
如果無限小變換(5)是系統的 Mei對稱性變換,且存在規范函數 GN=GN(t,q,q˙),滿足方程:
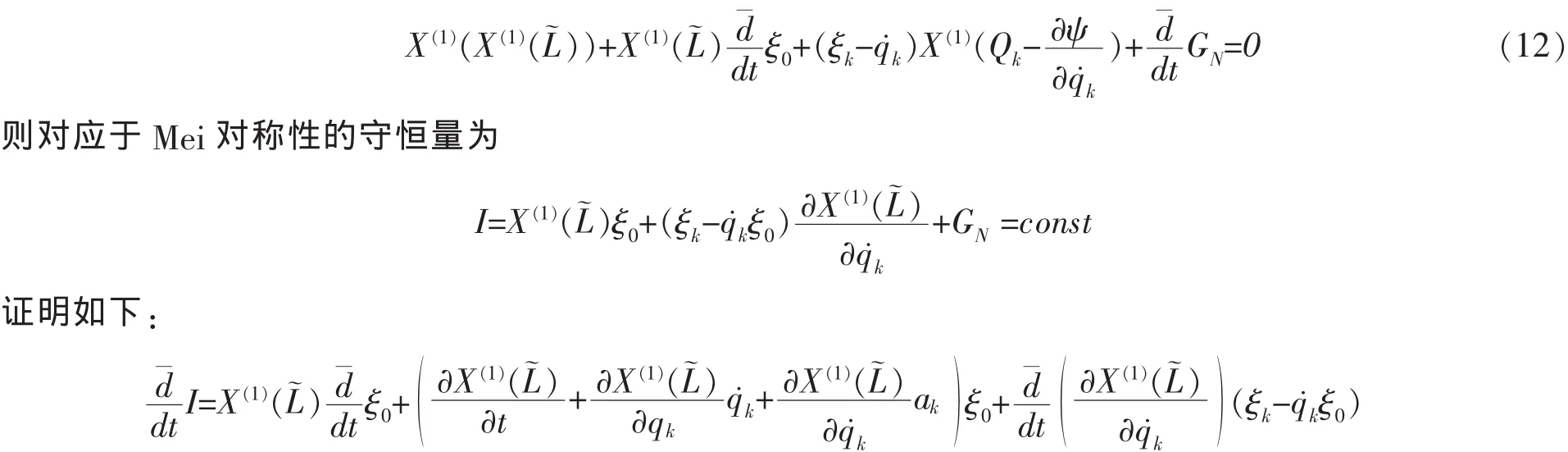
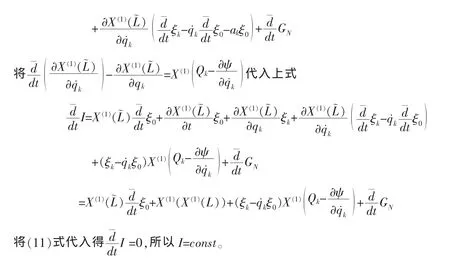
6 總結
本文中研究結果表明:群的無限小變換,在LRC電路系統同樣具有Noether對稱性,Lie對稱性,Mei對稱性,當其生成元ξ0,ξk滿足一定的確定方程時,便可獲得相對應的守恒量,從而可以開辟應用Lagrange力學來研究這些領域的新途徑。
[1]趙躍宇,梅風翔.力學系統的對稱性與守恒量[M].北京:科學出版社,1999.
[2]傅景禮,陳向煒,羅紹凱.Lagrange-Maxwell系統的 Lie對稱性與守恒量[J].固體力學學報,2000,21(2):157~160.
[3]張毅,葛偉寬.相對論性力學系統的 Mei對稱性導致的新守恒律[J].物理學報,2005,54(04):1464~1467.
[4]梅風翔,劉瑞,羅勇.高等分析力學[M].北京:科學出版社,1999.
[5]王其申.經典力學[M].合肥:中國科學技術大學出版社,2005.
SYMMETRIES AND CONSERVED QUANTITIES OF THE LRC CIRCUIT SYSTEM
Qian Hua-feng Wang Qi-shen
(School of Mathematics and Computation Science of Anqing Teacher College,Anqing Anhui 246011)
The important applications are obtained for the Lagrange mechanics in the class-mechanical system.Taken use of the Lagrange equation,we can deal with some the class-mechanical system questions.Used the Lagrange equation under the group infinitesimal transformations,the symmetries and conserved quantities of the LRC circuit system are obtained.
the class-mechanical system; LRC circuit; symmetry; conserved quantities
O302
A
1672-2868(2010)06-0057-05
2010-09-05
錢華峰(1973-),男,安徽桐城人。安慶師范學院數學與計算科學學院研究生。
責任編輯:宏 彬

