卡爾曼濾波粗差修正方法應用
齊公玉,邱衛寧,花向紅
(1.武漢大學 測繪學院,湖北 武漢 430079;2.武漢大學 災害監測與防治研究中心,湖北 武漢 430079)
卡爾曼濾波粗差修正方法應用
齊公玉1,2,邱衛寧1,2,花向紅1,2
(1.武漢大學 測繪學院,湖北 武漢 430079;2.武漢大學 災害監測與防治研究中心,湖北 武漢 430079)
基于標準卡爾曼濾波,提出對含有粗差的觀測值進行整體修正和局部修正。最后,通過工程實例驗證,兩種修正方法均能夠有效抵抗粗差的影響,并可獲得比標準卡爾曼濾波更準確的濾波結果。
卡爾曼濾波;粗差修正;應用
卡爾曼濾波理論作為一種重要的最優估計理論被廣泛用于各種動態數據處理中。其采用線性狀態方程描述系統,結合觀測方程,采用遞推形式計算系統的最優估值[1]。它無需存儲大量觀測數據,便可進行參數估計。但是,卡爾曼濾波容錯能力很差,觀測值中有很小的粗差,會使濾波發散,使濾波估值發生大的偏移。所以,如何有效地探測和修正動態測量數據中粗差觀測值是非常值得研究的問題。
目前,粗差的定位常用的方法有以均值漂移模型為基礎的粗差探測法和以污染誤差模型理論為基礎的抗差估計[2-3]等方法,但是,這些方法要求觀測網必須具有一定的幾何圖形強度和多余觀測數。在實際工程中,如水準檢測網中,一般多余觀測數很少,如果將含有粗差的觀測值剔除將使一些狀態參數無法得到估計。這樣就需要對含有粗差觀測值進行修正,而不能簡單的舍棄。本文將粗差修正分為兩類—整體修正和局部修正,并根據實際的工程數據,分析兩種方法均可以獲得比標準卡爾曼濾波更加準確的濾波結果,因此,這種方法的研究具有實際的工程應用價值。
1 標準卡爾曼濾波
設一線性系統的狀態方程和觀測方程為
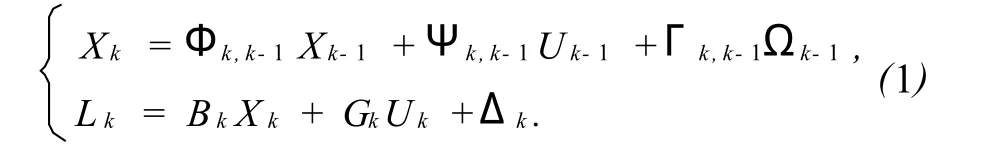
式中:Xk為狀態向量,Lk為觀測向量,Φk,k-1為狀態轉移矩陣,Uk-1為控制向量,一般不考慮,Γk,k-1,Bk為系數矩陣,Ωk-1為系統動態噪聲向量,Δk為觀測噪聲向量,其隨機模型為
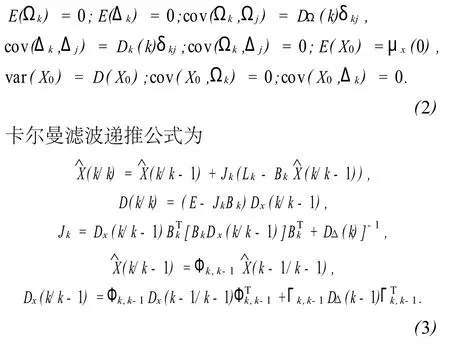
2 粗差探測方法
令
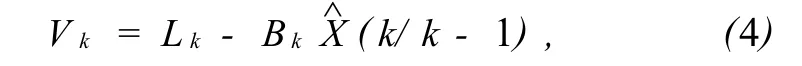
由統計性質可知,Vk是均值為0的高斯隨機量,根據式(4),可以得到其協方差陣為
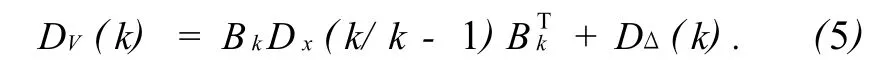
式中:Dx(k/k-1)為預測誤差協方差陣,DΔ(k)為觀測誤差協方差陣。
假定濾波模型是正確的,需要判斷觀測值是否存在粗差,根據文獻[4]中,構造檢驗統計量 Tk=VkTDV(k)Vk~χ2(nk,0),對于給定的顯著水平α,當Tk<χ2a時,認為濾波正常,反之認為濾波不正常,即觀測值存在粗差。
3 粗差修正
在判斷觀測值存在粗差后,粗差的修正可以分為2種方法,一種為整體修正,一種為局部修正。整體修正為對k期的觀測值統一進行迭代運算;而局部修正是對探測到的個別粗差觀測值進行迭代修正。
3.1 整體修正法
設k期的觀測值Lk,探測到存在粗差觀測,假設 k期以前濾波均正常,并且已經求得^X(k-1/k-1),則加入粗差修正過程的第k期卡爾曼濾波過程為
1)根據式(1)的狀態方程,可知 k期的預測值X^(k/k-1),并計算出其協方差陣;

5)迭代結束后,選擇修正后的L′k計算參數的濾波估值。
3.2 局部修正法
在文獻[5]中提出根據式(5)判別粗差觀測值的判別式為
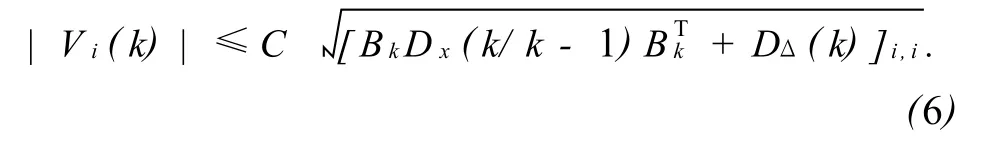
式中:i,i為對角線上第i個元素;Vi(k)為V(k)第 i個分量。C為常數,可根據實際物理背景確定。根據式(6),探查到含有粗差觀測值的具體位置。
設k期的觀測值Lk,探查到第 j個觀測值Lkj存在粗差,假設 k期以前濾波均正常,并且已經求得^X(k-1/k-1),則加入粗差修正過程的第 k期卡爾曼濾波局部修正過程如下:
1)根據式(1)的狀態方程,得到 k期的預測值X^(k/k-1),并計算出其協方差陣;
2)按照標準卡爾曼濾波進行計算,得到濾波結果^X(k/k);
Lk的修正值,將第 j個觀測值換為L′k中第j個值;
4)對步驟2)、3)進行迭代運算,并計算每次迭代 后 的 單 位 權 方 差 因 子 σ^2
5)迭代結束后,選擇最后修正后的 L′k計算參數的濾波估值。
4 實驗分析
為驗證本方法的計算精度,文中采用某一地表沉降監測項目中的對動態水準監測網數據進行處理。監測網中共有12個未知地表點D1~D12和1個已知點。數據采樣時間為3~4 d,共監測20期。本文對3期數據進行處理,根據前2期確定的初值,對第3期數據進行濾波。選取未知點的高程和高程的變化率為狀態參數,其中Δt=4。
濾波參數初值的選取:X0選取第2期高程平差結果。X˙0選取為第1期和第2期平差結果之差與數據采樣間隔的比值。X(0/0)=X0;DΩ=E;D(0/0)=E。狀態方程和觀測方程為
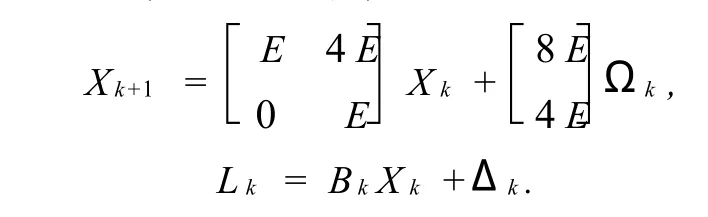
數據處理過程:首先,根據僅有偶然誤差時的觀測值進行粗平差得到結果作為真值。其次,在觀測值 H2,H9中分別加入5 cm的觀測誤差,用標準卡爾曼濾波及整體修正和局部修正法分別進行求解,并分別求出與真值的差值。最后,對數據結果進行比較,得出結論。
假設預測值準確,通過MA TLAB程序解算得到表1中的數據。

表1 數據計算結果比較
通過表1中數據比較,可以得到如下結論:
1)整體和局部修正方法都可以有效地抵抗粗差的影響,獲得比較接近平差值的濾波結果。
2)整體修正法比局部修正法收斂較快。
3)局部修正結果比整體修正總體上結果要準確。但是局部修正需要提前進行粗差定位。經檢驗,如果粗差定位時存在未被探測到的粗差觀測,則濾波結果會變壞。但是如果定位粗差觀測值多于實際的粗差觀測值,濾波結果仍然較好。
5 結束語
本文提出卡爾曼濾波在進行有粗差觀測值的濾波時發散的問題,基于此問題在標準卡爾曼濾波的基礎上,并在假定濾波模型正確后,將卡爾曼濾波粗差修正分為整體修正和局部修正兩方法,并給出各自的計算步驟。最后,將兩種方法應用于工程實際數據的解算中,通過與標準卡爾曼濾波比較計算可以得出,兩種修正方法在含有粗差時的濾波中均能夠有效抵抗粗差觀測值的影響,獲得比較接近真值的濾波結果。但從結果分析可以發現,兩種方法又有各自的優缺點。計算結果表明,卡爾曼濾波粗差修正方法具有實際的應用價值和研究價值。但如何快速準確的粗差定位仍需要進一步的研究。
[1]王秋平,陳 娟,王顯利,等,一種新的自適應非線性卡爾曼濾波算法[J].光電工程,2008,35(7):17-21.
[2]朱建軍,曾卓喬.污染誤差模型下的測量數據處理理論[J].測繪學報,1999(3):215-220.
[3]宋力杰,楊元喜.均值漂移模型粗差探測法與LEGE法的比較[J].測繪學報,1999(4):295-300.
[4]許國輝,張新長.卡爾曼濾波模型粗差的探測及其在施工變形中的測量[J].中山大學學報:自然科學版,2003,42(3):89-91.
[5]祝轉民,秋宏興,李濟生,等.動態測量數據野值的辨識與剔除[J].系統工程與電子技術,2004,26(2):147-149.
[6]劉大杰 ,于正林,陶本藻.形變測量動態數據的處理方法[M].北京:測繪出版社,1992:185-193.
[7]HAMPEL.Robust Statistics App roach Based on Influence[M].John Wiley Press,1986.
Themethod of grosserror modification in Kalman Filtering and itsapplication
Q IGong-yu1,2,Q IU Wei-ning1,2,HUA Xiang-hong1,2
(1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Hazard Monitoring and Prevention Research Center,Wuhan University,W uhan 430079,China)
M ethods of integralmodification and part modification are raised to modify gross error based on the standard Kalman Filtering.In the end,the resultsof an engineering examp le indicate that themethods can both effectively control the effects of gross error and obtain the more accurate results.
Kalman Filtering;gross error modification;app lication
P207
A
1006-7949(2010)01-0050-03
2009-04-22
國家863計劃資助項目(2008AA 12Z308);國土資源大調查項目(1212010914015);武漢市科技計劃資助項目(200760323113)
齊公玉(1986-),女,碩士研究生.
[責任編輯李銘娜]

