例說數學課堂的類比創新教學

● ●

(海鹽高級中學 浙江海鹽 314300) (臺州市第一中學 浙江臺州 318000)

例說數學課堂的類比創新教學

●王鵬鋒●湯香花

(海鹽高級中學 浙江海鹽 314300) (臺州市第一中學 浙江臺州 318000)

1 問題的提出

翻開普通高中課程標準實驗數學教科書，首先呈現的是教材的主編、北京師范大學劉紹學教授撰寫的“主編寄語”.在這篇寄語中，劉先生對為什么要學數學，如何才能學好數學等問題提出了自己的看法，并建議：在對數學有一個正確認識的基礎上，要摸索自己的學習方法學數學，做到類比地學、聯系地學.既要從一般概念中看到它的具體背景，不使概念“空洞”，又要在具體例子中想到它蘊含的一般概念，以使事物有“靈魂”．在日常的數學學習中，該如何類比、聯系一般概念與具體背景呢？

2 一個教學片斷

不等關系與相等關系都是客觀存在的基本數量關系，是數學研究的重要內容．建立不等觀念、處理不等關系與處理等量問題是同樣重要的．在處理問題的方式、方法上,兩者是否具有相似性？學生能否利用數學內容之間的內在聯系，特別是蘊含在數學知識中的數學思想方法，學習類比、推廣、特殊化、化歸等數學思考的常用邏輯方法，學會數學思考與推理，不斷提高數學思維能力？為此，筆者設計以下題組：

1.(1)已知x=2，y=3，求x+y與x-y的值；

(2)已知x+y=5，x-y=-1，求x與y的值．

2．(1)設實數x,y滿足1≤x≤2，3≤y≤4，求x+y與x-y的取值范圍；

(2)設實數x,y滿足4≤x+y≤6，-3≤x-y≤-1，求x與y的取值范圍．

對于這2個問題，學生的看法是：第(2)小題是第(1)小題的逆運算，問題2是由問題1類比得到的，因此不等式的解題方法可以參考等式的解題方法．但在嘗試解決問題時，學生們提出疑問：在等式運算中，條件與結論可以交換，但在不等式運算中，當結論變為條件時，所得結論卻與原來的條件不同，解題方法正確嗎？

問題意識指的是學生面臨需要解決的問題時的一種清醒、自覺，并伴之以強烈的困惑、疑慮及想要去探究的內心狀態．正是這種內心狀態驅使著學生積極地思維，不斷地產生解決問題的辦法，不斷地提出新的問題．

生B：類比加減消元法解方程，得到y的取值范圍縮小了．

師：x與y的取值范圍能繼續縮小嗎？

類比地學，能引發學生的學習動機，有助于學生批判性地思考，幫助學生重建知識結構．

生C：采用特值法．

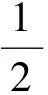
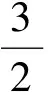
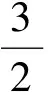
這說明生B的解答是正確的．

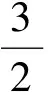
因此

1≤x-y≤3，

與已知-3≤x-y≤-1矛盾，這說明生A的解答是不正確的．

利用相等關系去分析不等關系，學生容易理解，但又產生了新的問題：在不等式的解題過程中，生A的每一個步驟都很合理，解答為什么是不正確的？

提出新的問題、新的可能性，從新的角度去看舊的問題，有助于學生聯系地學，從而找到新知識的生長點．

生D：在等式中，x與y的值是確定的，可以通過代入x的值去求y的值．而在不等式中，x與y之間存在的是一種不等關系，當x取得最大(小)值時，y并不能同時取得最大(小)值．生A解法的問題正在于此，由于忽略了x與y的相互制約關系，所得出的取值范圍比實際的范圍要大．生B的解法整體上保持了x與y的相互制約關系，從而得出的范圍是準確的．

3 體驗學習方法

筆者認為，學生要獲取重要的數學知識，更要體驗學習數學、研究數學的方法，做到類比地學、聯系地學．

3.1 問題拓展

在不等式求解過程中，必須在整體上保持x與y的相互制約關系，即根據不等式的性質，將所求代數式用已知代數式表示．因此學生容易將問題拓展為：

已知4≤x+y≤6，-3≤x-y≤-1，求3x+4y的取值范圍．

解法1由

3x+4y=

可得

解法2設3x+4y=m·(x+y)+n·(x-y)，

則

解得

3.2 問題創新

聯系等式中的運算：加、減、乘、除、乘方、開方，學生會類比不等式的加減運算性質，嘗試得到不等式的乘、除、乘方、開方的運算性質，將問題創新為：

類比加減運算的解法，學生嘗試將問題化歸為如何在整體上保持x與y的相互制約關系，即根據不等式的性質，將所求代數式用已知代數式表示．得到如下解題過程：

因為

又

所以

學生通過體會各種運算之間的聯系與區別，總結數學學習的經驗，在課堂生成中領悟數學研究的方法．

3.3 問題延伸

例1設函數f(x)=x3+3bx2+3cx有2個極值點x1,x2，且x1∈[-1,0],x2∈[1,2].

(1)求b,c滿足的約束條件，并在坐標平面內畫出滿足這些條件的點(b,c)的區域；

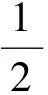
(2009年全國數學高考試題Ⅰ)

解(1)略．

(2)由題意得

又

(2)

消去b可得

因為

x2∈[1,2]，且c∈[-2,0],

所以

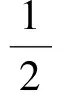
另解由題意得

x1+x2=-2b,x1·x2=c,

因為x1∈[-1,0],x2∈[1,2],所以