非貫通節理巖體多層結構模型研究Ⅰ:理論部分

彭從文 曹 芳

(長江大學城市建設學院，湖北 荊州 434023) (荊州市江漢建設工程施工圖審查事務所，湖北 荊州 434020)

非貫通節理巖體多層結構模型研究Ⅰ:理論部分

彭從文 曹 芳

(長江大學城市建設學院，湖北 荊州 434023) (荊州市江漢建設工程施工圖審查事務所，湖北 荊州 434020)

巖體的力學性狀與其結構面分布及特性有關，對于非貫通節理巖體，當節理定向排列,特別是巖橋長度遠小于節理長度時，一般發生共面剪切破壞。針對壓剪荷載下非貫通節理巖體，將共面節理及其間巖橋構成的剖面稱為等代結構面，結合斷裂力學方法，研究了非貫通節理巖體多層結構模型。模型包括彈性變形、滑移、開裂直至貫通等階段。等代結構面剪切強度由節理與巖橋2部分組成，其中，節理強度表現為基本摩擦角與粗糙角，巖橋強度表現為等效粘聚力。節理貫通時，退化為Zienkiewicz節理巖體模型。

非貫通節理；巖體；多層結構模型；斷裂力學

巖體的力學特性取決于結構面的分布與力學性態。巖體結構面包括微裂隙、節理、層面、斷層及整個斷裂帶等，其中，非貫通節理面在巖體中大量存在。非貫通節理巖體變形破壞有以下幾個特點：①荷載作用下,裂紋一般沿裂尖擴展，裂紋類型有翼狀裂紋、次級裂紋；②破壞模式有張拉破壞、剪切破壞及復合破壞等，其類別與法向應力及節理空間相對位置有關，對于共線節理，一般發生共面剪切破壞；③變形破壞過程具有明顯的階段性。隨荷載增加,經歷線彈性變形、節理面錯動、節理起裂、擴展直至貫穿巖橋等過程。

非貫通節理巖體的計算方法主要采用等效連續體方法，包括基于解析方法的變形等效方法、能主量等效方法以及基于數值解的單元體法與漸近展開法。考慮節理擴展時，常采用損傷力學方法。等效連續體模型沒有考慮節理個體性狀差異，適用于節理在空間隨機分布情形，當節理定向排列,特別是巖橋長度遠小于節理長度時，一般發生共面剪切破壞，巖體沿節理面滑移[1]。此種情況下，巖體性狀主要取決于節理及其巖橋組成的擬結構面。節理巖體一般有多組結構面，不同的結構面處于不同的受力狀態，對巖體性狀有不同的影響。Zienkiewicz等[2]針對貫通節理巖體提出了多層結構模型。下面，筆者考慮節理面細觀形態及巖橋阻力的影響，將巖體破壞考慮為由非貫通結構面向貫通結構面轉化的過程，建立了共面非貫通節理巖體多層結構模型。

1 概念模型

圖1 非貫通節理巖體宏細觀結構示意圖

研究對象為壓剪荷載下非貫通節理巖體。巖體中含一組或多組節理，將共面節理及其間巖橋構成的剖面稱為等代結構面(以下稱結構面)，如圖1(a)中AB所示。一般情況下，平面模型有2組結構面，空間模型有3組結構面，計算模型有如下假定：①節理為齒狀、無厚度、無充填物、初始閉合；②節理共線，巖橋長度遠小于節理長度，受荷時發生共面剪切破壞；③受荷后節理經歷彈性變形、滑移、開裂直至貫通等階段；④巖體非線性變形來源于結構面，總非線性變形為各層結構面非線性變形之和；⑤結構面剪切強度由節理與巖橋2部分組成，節理強度表現為基本摩擦角與粗糙角(突臺傾角)，巖橋強度表現為等效粘聚力，其值隨著裂紋擴展不斷弱化直至貫通時為零；⑥巖體總應變為巖塊應變與節理應變之和。

2 節理滑移模型

圖2 節理面形態示意圖

(1)

寫成張量形式有:

(2)

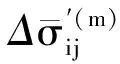
假定裂紋面法向與總體Z坐標夾角為ψ；局部X坐標在總體坐標XY平面內,且與總體Y坐標夾角為θ。總體坐標節理巖體應變為:

(3)

將巖塊與節理應變相加,得到節理巖體平均應變為:

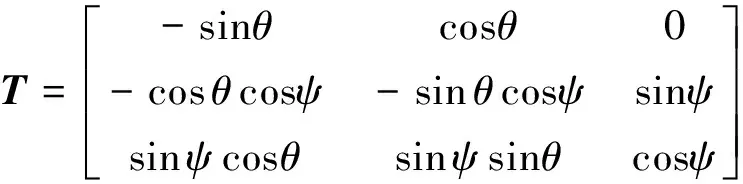
(4)

3 節理擴展模型

圖3 節理開裂斷裂力學模型

對于共線非貫通節理，一般發生共線剪切破壞[4～6]，假定裂紋沿已有節理面擴展，采用Ⅱ型斷裂韌度作為開裂準則，研究非貫通節理多層結構模型。模型不考慮裂紋增長的亞臨界狀態(即過程區)，也不考慮裂紋的非穩定擴展。

3.1節理開裂準則

當剪應力超過等代結構面抗剪強度后，裂紋開始擴展。巖橋的斷裂力學示意圖如圖3所示。巖橋長度為2b,節理中心距為2w,在遠場應力作用下,Ⅱ型應力強度因子[7]為:

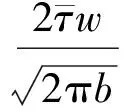
(5)

考慮裂紋面的摩擦作用力時,式(5)可改寫為(受壓為負):

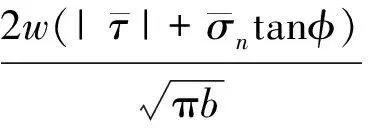
(6)

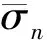
采用斷裂力學方法，應力強度因子KII等于斷裂韌度KIIC時裂紋開始擴展，有：

(7)

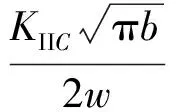
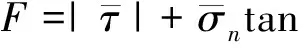
(8)

3.2裂紋流動勢

采用非關聯流動法則，流動勢取G為：

(9)

材料剪脹由不平整界面引起。對于非貫通節理巖體，節理貫通前，剪脹性與巖橋有關，剪脹性不明顯。貫通后與界面突臺構形及圍壓有關，剪脹應較貫通前增大許多。

3.3裂紋演化方程

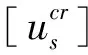
(10)

式中，2b0為初始巖橋長度；η為試驗參數。

3.4本構關系

多層結構模型認為結構非線性變形主要由結構面的變形組成，計算非線性變形時，模型以結構面為對象，而非單元體。當巖體中只有一組節理時，多層結構模型描述的是橫觀各向同性材料的本構關系；當巖體中沒有節理時，該模型便成為各向同性材料的本構模型。

1)單層結構 節理巖體應變dε分為彈性應變dεes(含滑移)與節理開裂應變dεcr：

dε=dεes+dεcr

(11)

將節理考慮為無厚度結構面，節理開裂相對位移微量[8]為：

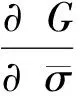
(12)

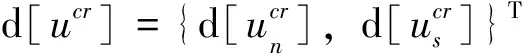
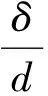
(13)

由應力應變關系：

(14)

及一致性條件：

(15)

得：

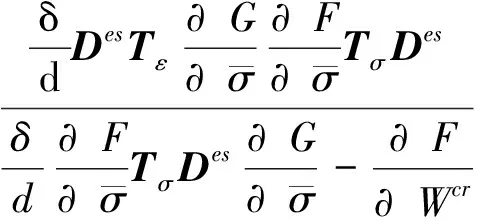
(16)

(17)

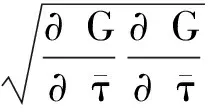
當節理貫通時，式(16)中硬化項Wcr為零，模型中尺寸參數消失，退化至Zienkiewicz節理巖體模型。

2)多層結構 對于多組節理同時開裂，應力增量為：

dσ=Desdεe=Des(dε-dεcr(1)-dεcr(2)-dεcr(3)-…)

(18)

由式(13)得每組節理開裂應變，代入式(18)得:

(19)

結合m個一致性條件:

可得本構關系。假定有2組節理，本構矩陣為:

(20)

式中:

4 結 語

以壓剪荷載下非貫通節理巖體為研究對象，將共面節理及其間巖橋構成的剖面稱為等代結構面，結合斷裂力學方法推導了非貫通節理巖體多層結構模型。模型包括彈性變形、滑移及開裂等階段，考慮了節理細觀形態，等代結構面強度由節理及巖橋共同組成，節理貫通的過程就是巖橋等效粘聚力逐漸減小的過程。模型假定發生共面剪切破壞，適用于巖橋長度遠小于節理長度的情形。當節理貫通時，巖橋等效粘聚力為零(或小值)，模型中尺寸參數消失，退化至Zienkiewicz節理巖體模型。

[1]Kemeny J. the time-dependent reduction of sliding cohesion due to rock bridges along discontinuities: a fracture mechanics approach[J]. Rock mechanics and rock engineering, 2003,36(1):27～38.

[2] Zienkiewicz O C,Pande G N.Time Dependent Multilaminate Model of Rocks-A Numerical Study of Deformation and Failure of Rock Masses[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1977,1:219～247

[3] Yoshida H, Horii H. Micromechanics-based continuum model for a jointed rock mass and excavation analyses of a large-scale cavern[J].International Journal of Rock Mechanics amp; Mining Sciences, 2009, 41: 119～145.

[4]Robina, Wong H C, Chau K T. Crack Coalescence in a Rock-like Material Containing Two Cracks[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 147～164.

[5] Mughieda O. Fracture mechanisms of offset rock joints-A laboratory investigation[J]. Geotechnical and Geological engineering, 2004, 22: 545～562.

[6] Mughieda O. Stress Analysis for Rock Mass Failure with Offset Joints[J]. Geotechnical and Geological Engineering, 2008, 26:543～552.

[7] Rooke D, Cartwright D. Compendium of stress intensity factors[M]. London:H M S O,1976.

[8] Cai M, Horri H. A constitutive model and FEM analysis of jointed masses[J]. International Journal of Rock and Mining Sciences amp; Geomechanical Abstracts,1993,30(4):351～359.

[編輯] 洪云飛

2010-06-22

國家自然科學基金資助項目(51078331)。

彭從文(1969-)，男，1990年大學畢業，博士，副教授，現主要從事準脆性材料細觀斷裂機理及多層結構模型方面的教學與研究工作。

TU452

A

1673-1409(2010)03-N131-05