基于重要抽樣的強弱鏈安全系統失效概率計算

鎖 斌,程永生,曾 超,李 軍

(中國工程物理研究院電子工程研究所,四川綿陽 621900)

0 引言

要害系統[1]一旦發生安全性事故,后果往往是災難性的。為了確保要害系統在火燒、跌落、雷擊等意外環境中的安全性,美國Sandia國家實驗室提出了“第一原理”[2],并在此基礎上形成了“增強引爆安全”(ENDS,Enhance Nuclear Detonation Safety)技術[3]。

ENDS系統中最重要的部件是強鏈和弱鏈。一旦發生火燒、跌落等意外事故,必須保證弱鏈先于強鏈失效,實現事故窒息,從而保證整個系統的安全性,否則就認為系統安全性失效。

目前,ENDS系統的設計、評估技術在國外已經比較成熟,但由于技術壁壘等原因,未見詳細、系統的報道。國內相關單位已經具備了ENDS系統的設計能力,但對ENDS系統在異常環境下安全性評估方面的工作尚待深入。

火燒是最常見的異常環境之一。在火燒事故中,溫度沖擊下強弱鏈安全系統的失效概率計算中,傳統的蒙特卡洛仿真方法(Monte Carlo Simulation,MCS)存在抽樣效率低、收斂較慢的缺點。針對這些不足,本文將改進的蒙特卡洛方法——重要抽樣方法(Importance Sampling,IS)引入到失效概率的計算中,以期減小抽樣次數,提高運算效率和精度,為ENDS系統的安全性評估提供一定的參考。

1 強弱鏈安全系統

強鏈、弱鏈是 ENDS系統中的重要部件。ENDS系統主要由禁區(Exclusion region)、強鏈(Strong Link)、弱鏈(Weak Link)和獨特碼(Unique Signal,UQS)組成[3],如圖1所示。

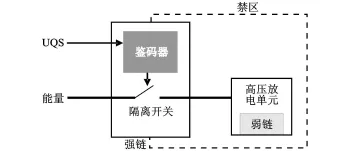
圖1 ENDS系統基本要素構成圖Fig.1 Basic elements of ENDS system

禁區是一種特殊材料構成的能量屏障,將安全關鍵件保護起來。強鏈則守住禁區的入口,強度與禁區相當,禁止一切非授權能量進入禁區,只有輸入正確的授權UQS才能使強鏈閉合。弱鏈則是在異常環境的強度可能超過強鏈和禁區的承受能力時,以一種安全的、可以預料的方式先于強鏈失效,從而保證整個系統的安全性。

在溫度沖擊下,由于強、弱鏈的結構、材料和安裝位置不同,因此隨著時間的推移有著不同的溫度變化規律。另外,由于強、弱鏈裝置的復雜性、加工工藝存在隨機不確定性等,導致對強、弱鏈的失效溫度的認識帶有不確定性。通過實驗和Ansys熱傳導仿真等方法,可以得到強、弱鏈時間-溫度曲線和失效溫度的分布規律。溫度沖擊下強、弱鏈安全系統的失效概率(Failure Probability under Temperature Impulsion,FPTI)被定義為強鏈先于弱鏈失效的概率。

2 失效概率計算的重要抽樣方法

當溫度函數和失效溫度概率密度函數較為簡單時,FPTI的計算相對容易。但當被積函數較為復雜時,尤其是溫度函數的反函數難以求解時,通常的數值積分方法就會變得很困難。而蒙特卡洛方法的本質則在于隨機模擬,因此在用于多重積分的數值計算時,誤差與積分維數和積分區域無關,從而廣泛的應用于失效概率的分析[4-5]。

然而,蒙特卡洛方法的顯著缺點是抽樣效率較低,對于高維稀有失效概率計算的工作量很難為工程所接受。改進的蒙特卡洛方法——IS方法則可以較好地克服這個缺點。

IS方法的主要思想是通過尺度變換(Change of Measure,CM)來修改決定仿真輸出結果的概率測度,使本來發生概率很小的稀有事件頻繁發生,從而加快仿真速度,能夠在較短地時間內得到稀有事件[6-7]。

IS方法的關鍵是選擇合適的重要抽樣密度函數,以有效地減少方差,且只需要很少的樣本數便可以得到的一個可靠的估計;否則IS方法的效率可能很差。

目前,尋找最優重要抽樣密度函數的方法有很多種,如極小化方差法(Variance Minimization,VM)[8-10]、極小化交叉熵法(Cross Entropy,CE)[11-12]及其他方法[13-14]。

本文采用最常用的一種選擇重要抽樣密度函數的方法,即將抽樣中心平移到設計點(極限狀態域上距離標準正態空間原點最近的點),方差不變,即以設計點為均值、原密度函數的方差為方差的正態密度函數作為重要抽樣概率密度函數。這樣,抽樣時大量的樣本點落在設計點附近,在失效面的非線性程度不是很高的情況下,抽樣效率可達50%左右。對于失效面的非線性程度較高的情況,也可以達到較好的效果。基于重要抽樣方法計算FPTI的基本算法流程圖如圖2所示。

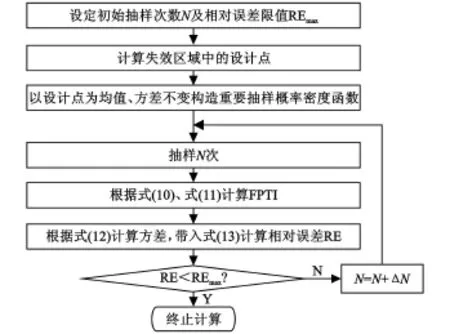
圖2 基于重要抽樣方法計算FPTI流程圖Fig.2 Flow Chart of Calculation of FPTIBased on IS Method

3 理論推導

設已知強、弱鏈的時間(t)-溫度(T)函數分別為TSL(t)和TWL(t),如圖3所示。失效溫度的概率密度函數分別為PDFSL(T)和PDFWL(T)。假設TSL(t)和TWL(t)相互獨立。

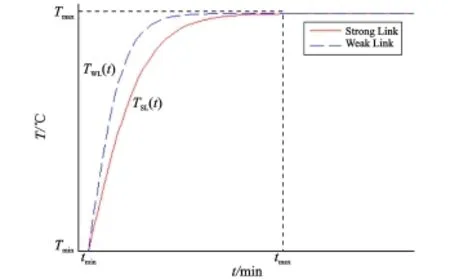
圖3 強鏈、弱鏈時間-溫度曲線Fig.3 Time-Temperature Curve of Strongand Weak Link

強、弱鏈的失效溫度分別為TF_SL和TF_WL,失效的時刻分別為tF_SL和tF_WL。起始溫度和最高溫度分別為 Tmin和Tmax,相應的時刻為tmin和 tmax,則失效概率FPTI的集合可定義為:

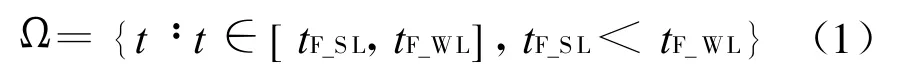
集合 Ω可以表示為:

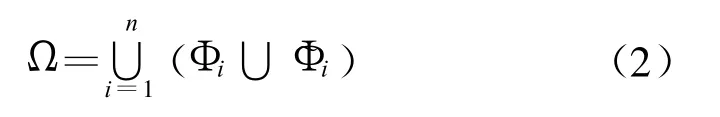
其中:

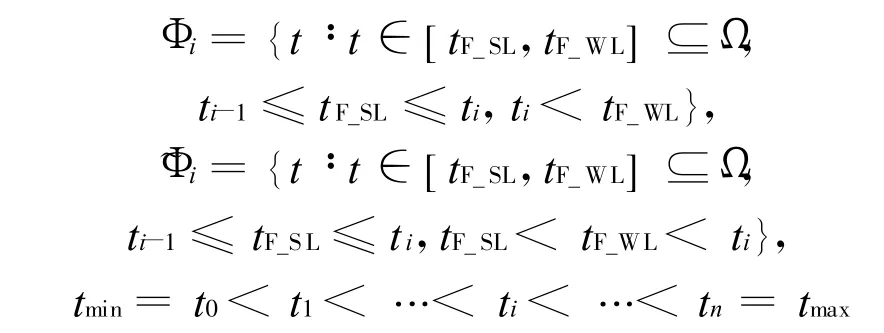
則失效概率為:

對于 i=1,2,…,n,有 :

由式(4)、式(5)可得:

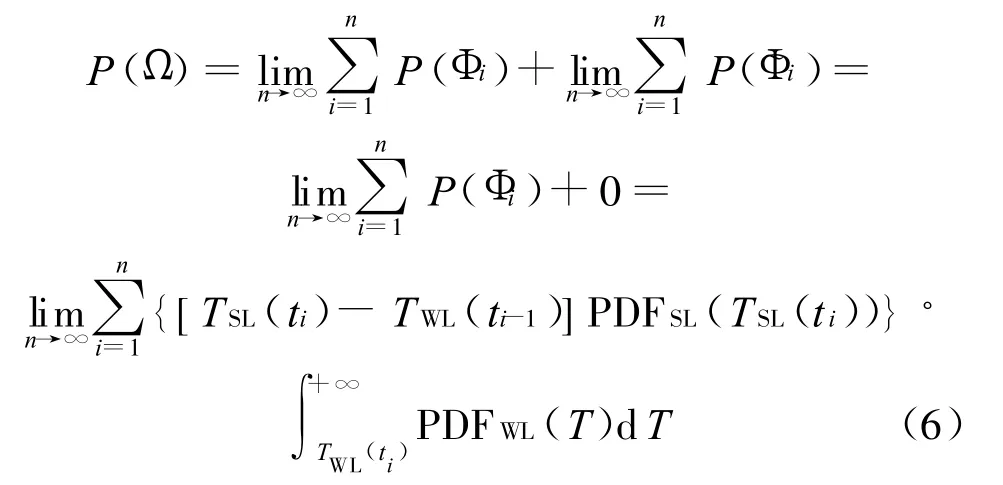
由式(6)可得:

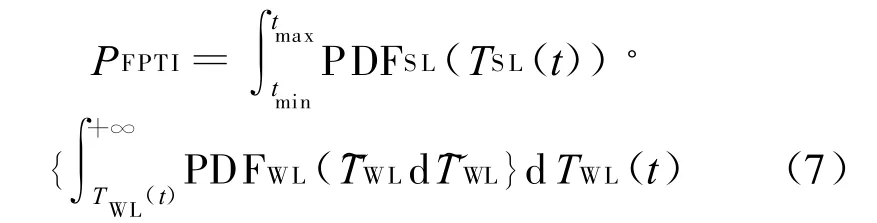
由如下積分變換公式[4]:

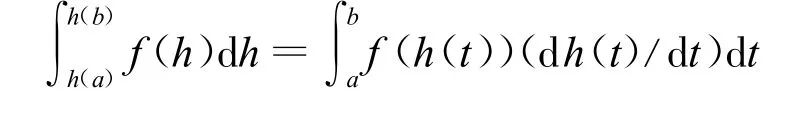
式(7)可改寫為:

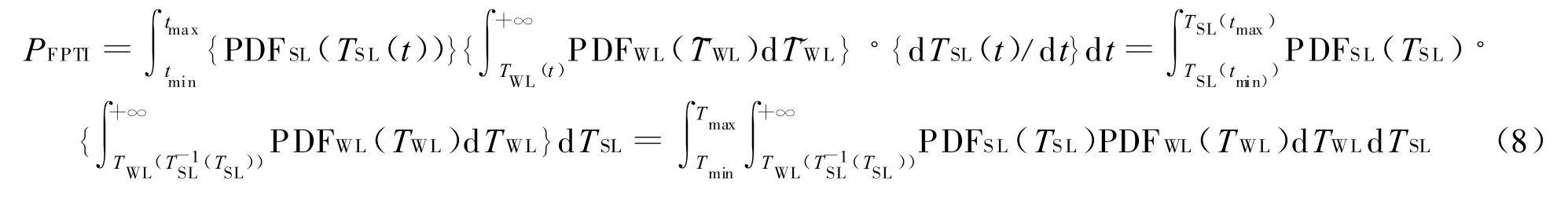
為便于采用重要抽樣方法,式(8)可改寫為:

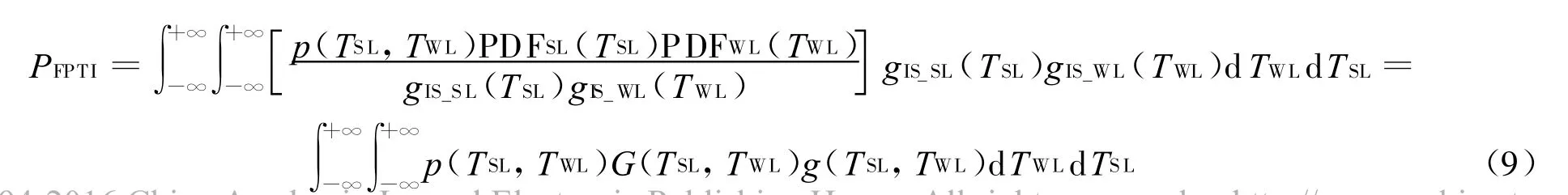
式中:

G(TSL,TWL)稱為似然比函數,g(TSL,TWL)為任意的概率密度函數,稱為重要抽樣密度函數。

根據IS方法的原理[7-8]可知PFPTI的無偏估計為:

變異系數(Coefficient of Variation)即相對誤差(Relative Error,RE)為:

4 實例仿真

設強、弱鏈的時間-溫度函數分別為[15]:

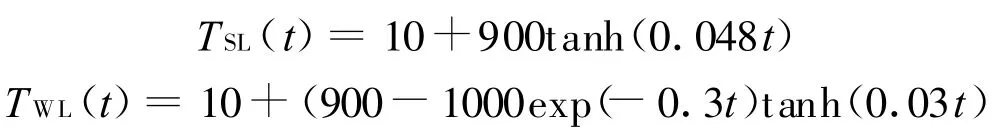
強、弱鏈的失效溫度服從正態分布:

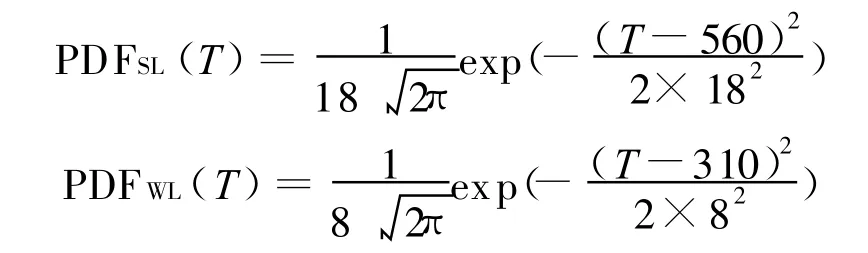
利用第2節中的重要抽樣方法計算出失效概率和相對誤差,結果列于表1。作為對比,表中也列出了標準MCS方法的計算結果。

從表1中可以看出,IS方法的抽樣效率明顯高于MCS方法,在相對誤差同樣為1.5%左右時,IS方法只需要4×105次抽樣,而MCS方法則需要2×107次左右的抽樣次數才能達到,抽樣次數遠大于前者。

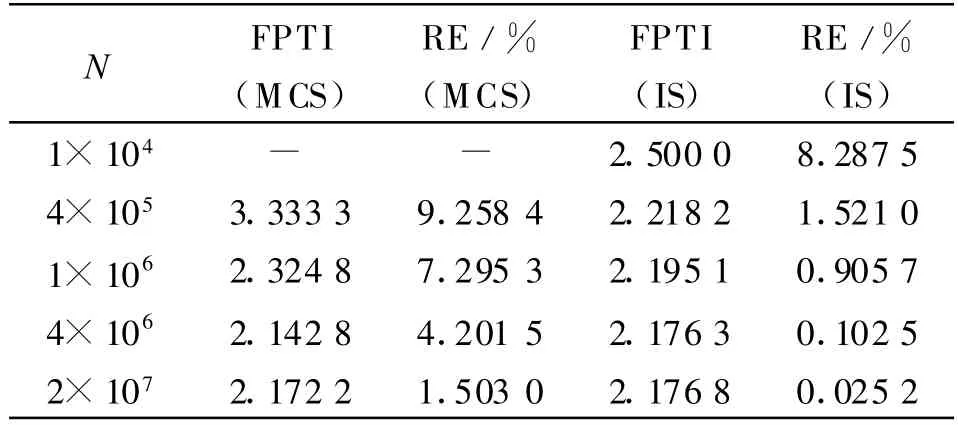
表1 MCS和IS數值仿真的失效概率和相對誤差Tab.1 Failure Probability and Relative Error of MCS and IS Methods

5 結論

本文提出了基于重要抽樣的強弱鏈安全系統失效概率的計算方法。以溫度沖擊下強弱鏈安全系統失效域中的設計點為均值、方差不變構造了重要抽樣概率密度函數,給出了相對誤差的計算方法,并結合一個實例進行了數值仿真。仿真表明:與傳統蒙特卡洛法相比,重要抽樣方法效率更高、誤差更小。

[1]Randall Gary T.High consequence system surety process description,SAND94-3223[R].US:Sandia National Laboratories,1995.

[2]Cooper J Arlin.System safety based on a coordinated principle-based theme,SAND98-1590C-PF.2[R].US:Sandia National Laboratories,1998.

[3]Dvorack M A,Jooes T R.System safety assessments combining first principles and model based safety assessment methodologies,SAND98-0162C[R].US:Sandia National Laboratories,1998.

[4]金治明,羅建書.應用數學的現代基礎[M].長沙:國防科技大學出版社,1998.

[5]王敏,王航宇.蒙特卡羅方法在集成電路可靠性分析中的應用[J].探測與控制學報,2008,30(4):63-66.WANG Min,WANG Hangyu.Application of monte carlo method in assessment of the integrated circuit reliability[J].Journal of Detection&Control,2008,30(4):63-66.

[6]周泓,邱月,吳學靜.基于重要抽樣技術的稀有事件仿真方法[J].系統仿真學報,2007,19(18):11-14.ZHOU Hong,QIU Yue,WU Xuejing.Rare event simulation method based on importance sampling technology[J].Journal of System Simulation,2007,19(18):11-14.

[7]謝國鋒,童節娟,何旭洪,等.用 M onte Carlo方法計算HTR-10余熱排出系統物理過程的失效概率[J].核動力工程,2008,29(2):85-87.XIE Guofeng,TONG Jiejuan,HE Xuhong,et al.Calculation of physical failure probability of HTR-10 residual heat removal system by M onte Carlo method[J].Nuclear Power Engineering,2008,29(2):85-87.

[8]Au S K,Beck J L.Important sampling in high dimensions[J].Structural Safety,2003,25(2):139-163.

[9]Biondini G,Kath W L,et al.Importance sampling for polarization-mode dispersion[J].IEEE Photon Tech Lett,2002,14(3):310-312.

[10]Sandmann,Werner.Rare event simulation methodologies and applications[J].Simulation,2007,83(11):749-750.

[11]Ridder Ad,Rubinstein Reuven R.Minimum cross-entropy methods for rare-event simulation[J].Simulation,2007,83(11):769-784.

[12]Qiu Yue,Zhou Hong,et al.An importance sampling method with applications to rare event probability[C]//IEEE International Conference on Grey Systems and Intelligent Services.US:GSIS 2007:1 381-1 385.

[13]Nicola VF,Shahabuddin P,Nakayama MK.Techniques for fast simulation of models of highly dependable systems[J].IEEE Transaction on Reliability,2001,50(3):246-64.

[14]Shahabuddin P.Importance sampling for the simulation of highly reliable Markovian systems[J].Manage Science,1994,40(3):333-52.

[15]Bohn M P.P-race users guide,SAND96-1 762[R].US:Sandia National Laboratories,1996.