船舶阻力計算BP神經網絡的研究*

陳愛國 葉家瑋 蘇 曙

(廣州航海高等專科學校輪機系1) 廣州 510725) (華南理工大學土木與交通學院2) 廣州 510640)

船舶 的計算,由于問題的復雜性,目前還沒有成熟 理論的公式,一般在船舶線型確定時可通過 實驗來確定,但在設計的初期或并不準備作 實驗時,只能進行阻力近似計算.阻力近似計 常用方法一般都是通過查閱大量圖表的方式來進行計算,工作量大且精度低.

Lippm ann[1],Funahashi[2],Hornik[3]等人對神經網絡的研究已表明:3層以上的前向神經網絡能以任意精度逼近任何非線性性函數,因此采用多層前向神經網絡來逼近以船型參數和速度流體參數為自變量的船舶阻力函數在理論上是可行的.為此本文采用系列60船模實驗數據作為樣本,由于作為前向神經網絡核心的誤差反傳BP網絡在函數逼近上具有優越的性能,本文力圖通過實驗建立出性能卓越的3層BP神經網絡船舶阻力計算系統.

1 數據樣本及處理

在系列60的計算中,平板摩擦阻力系數C f采用桑海公式計算,粗糙度補貼系數取0.4×10-3,其剩余阻力由船模試驗確定,剩余阻力的輸入數據包括3個船型參數和1個速度參數[4-5].船型參數為:方形系數C b,船長型寬比L/B,型寬吃水比B/H.輸入的速度參數有2種,分別對應不同的輸出參數:速長比對應的輸出為每噸排水量的剩余阻力系數C R;弗氏速率系數對應的輸出為弗氏阻力系數,由于后者在船舶初步設計時對船型的比較非常有用,其應用更受推薦,因此本文輸入的速度參數采用弗氏速率系數對應地輸出采用弗氏阻力系數.

系列60共用45個船模,共有數據838組.為檢驗網絡的泛化能力,隨機選取全部數據組中的629組作為訓練數據,另209組作為檢驗數據.采用訓練與檢驗神經網絡時輸出與目標的相關系數、回歸直線、最大相對誤差、平均相對誤差中的差值來衡量網絡的性能.

2 三層神經網絡結構設計

由上面的分析可知該BP神經網絡的輸入層為4個神經元,輸出層為1個神經元,設隱層神經元數為R,則其結構如圖1所示.

為選取合適的隱層神經元數R,傳遞函數g1(·),g2(·),性能函數E(·)和訓練函數,分別對之進行試驗.

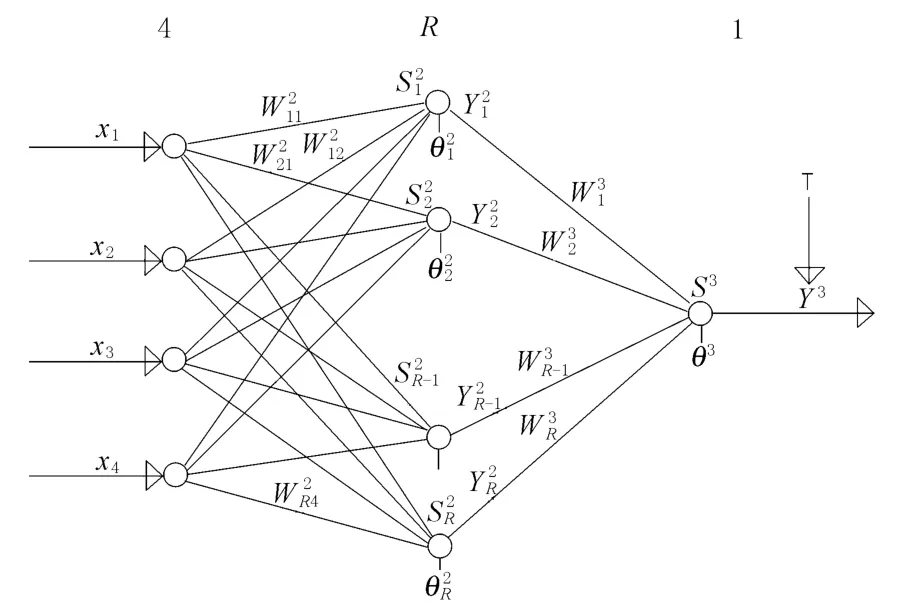
圖1 船舶阻力計算3層BP神經網絡結構圖

2.1 訓練函數和性能函數的確定

為確定該神經網絡的訓練函數,經初步試驗決定采用15個神經元的隱層,隱層傳遞函數g1(·)采用 tansig,輸出層傳遞函數g2(·)采用purelin,最大訓練次數采用1 000,由于數據量較大,采用批處量訓練方式,用網絡輸出數據與目標的相關系數(在多次訓練采用較好的相關性數據)來衡量訓練結果,從實驗結果看,普通訓練函數traingd和 traingdm收斂性差,而且增加最大訓練次數,也不能提高相關系數;快速訓練函數中,有彈回的BP算法trainrp比自適應修改學習率算法traingda和traingdx要好;其他的算法都可達到較高的計算精度,尤其是 traincgb,trainlm,trainbr.最好的是 trainbr,其訓練的相關系數和檢驗的相關系數不但最大,而且兩者相差最小,這是由于應用其他訓練函數時,網絡的性能函數E(·)是采用m se,如式(1),其中 N訓練樣本數,而trainbr作為規則化的調整方法是采用m sereg作為性能函數,如式(2)和式(3)所示,其范化能力更好.因此本試驗的神經網絡選用trainbr規則化的訓練方法,對應地采用m sereg作為性能函數.

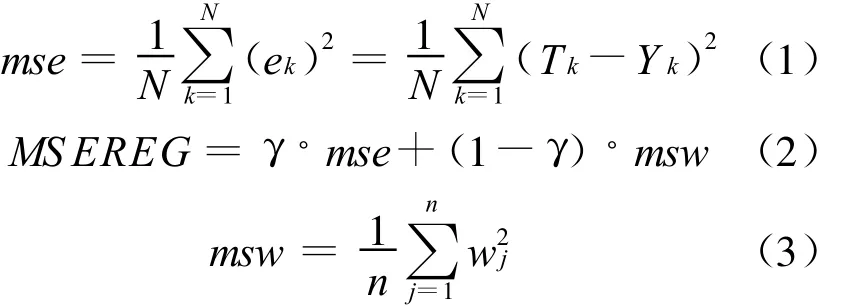
2.2 傳遞函數的確定

為確定該神經網絡隱層和輸出層的傳遞函數,仍采用15個神經元的隱層,最大訓練次數采用1 000,采用trainbr訓練函數,用網絡輸出數據與目標的相關系數(在多次訓練中采用較好的相關性數據)來衡量訓練結果.對BP網絡應使用可微的函數作傳遞函數,對本項目不適合使用satlin,satlins,tribas,hard lim,hard lims等帶水平線的非光順函數[6],因此本實驗對常用的 tansig,purelin,logsig進行組合實驗,并對采用 radbas進行了2組實驗,實驗結果如表1.

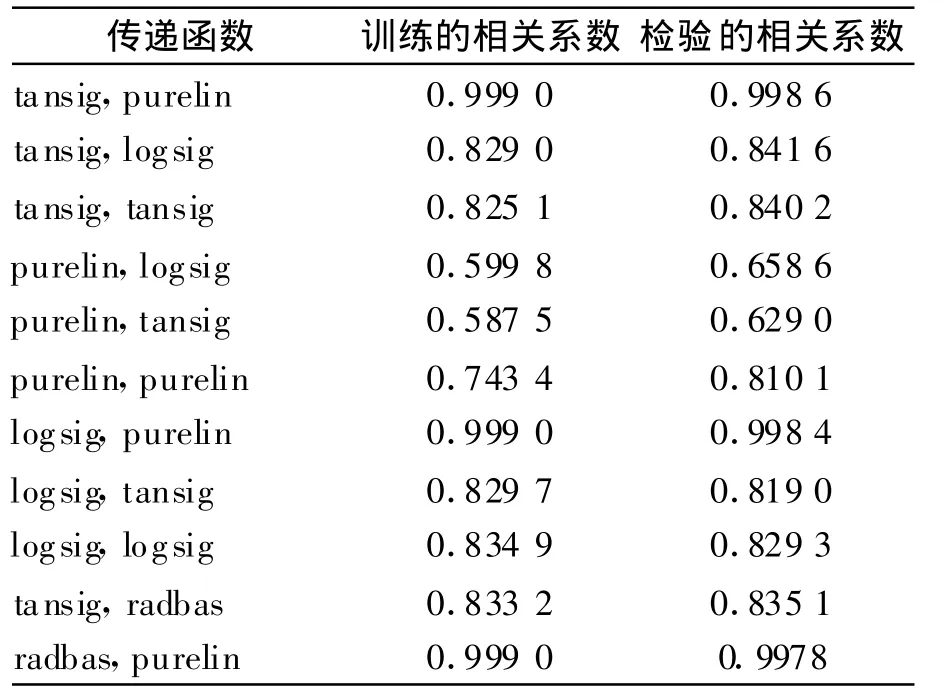
表1 傳遞函數實驗結果

從實驗結果可以分析得出,輸出層采用logsig或tansig相關系數不高;隱層的傳遞函數采用purelin不合適,網絡輸出數據與目標的相關系數最小,對于使用purelin,purelin傳遞函數,由于是純線性變換對非線性系統逼近能力差;而據實驗結果,隱層傳遞函數采用tansig或logsig,輸出層傳遞函數采用purelin可以很好地達到函數逼近,而且輸出數據與目標數據的回歸曲線與理想回歸曲線幾乎重合,對radbas的實驗表明,對本項目,該函數同樣不適于作輸出層傳遞函數,當進行 radbas,purelin組合時也可達到較好的結果,但檢驗結果相關性比前兩者稍差,從進一步的實驗結果看,采用 tansig、purelin作傳遞函數比采用logsig,purelin要稍好一些.

2.3 隱層神經元數試驗

由上面試驗結果,對該神經網絡隱層神經元數進行實驗,隱層傳遞函數采用tansig,輸出層傳遞函數采用purelin,最大訓練次數采用1 000,采用trainbr訓練函數,用網絡輸出數據與目標的相關系數和最大相對誤差來衡量訓練結果,編制程序,得到相關系數、最大相對誤差、平均相對誤差隨神經元數的變化曲線如圖2所示.

由圖2可知,隨神經元數的增加,相關系數越來越大、最大相對誤和平均相對誤差越來越小,但當神經元數達到15以后,變化很慢了.

2.4 采用預先數據處理訓練網絡

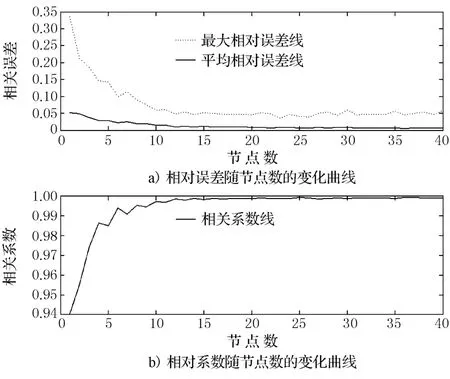
圖2 相關系數最大相對誤差和平均相對誤差隨隱層神經元數變化曲線

從上述實驗可知,增加隱層神經元數可提高神經網絡的性能,但由于檢驗數據與訓練數據一樣都來源于原始實驗數據,對B/H僅有2.5,3.0,3.5 3個數值,對C b,L/B也只有有限的幾個取值,當隱層神經元數過多時,將導致對某一參數在有限的幾個取值附近具有高的精度,但在其他值則有很大的波動,這與實際情形不符.如針對23隱層神經元的神經網絡,對C b=0.65,船長型寬比L/B=7.25,弗氏速率系數○k=1.4,弗氏阻力系數○C對B/H的變化曲線如圖3所示,顯然,此時曲線失真.同樣地對15隱層神經元的神經網絡繪制的曲線如圖4所示,則其插值曲線是較平順的.

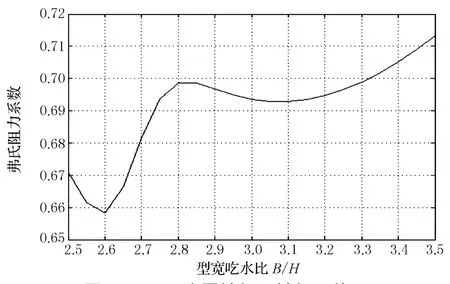
圖3 用23隱層神經元神經網絡繪制的○k對B/H的變化曲線

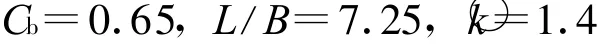
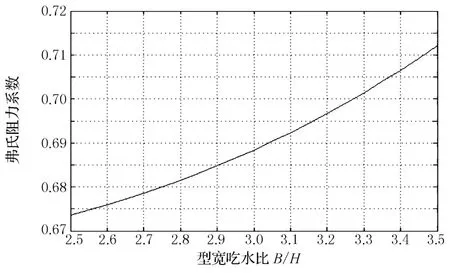
圖4 用15隱層神經元神經網絡繪制的○k對B/H的變化曲線

因此,為了提高網絡的逼近能力和降低相對誤差,對輸入樣本采用預先數據處理的方式,將輸入向量和目標向量的值量化到[-1,+1]內,進一步訓練結果如表2所列.

表2 預先數據處理訓練結果

2.5 船舶阻力最佳BP神經網絡的確定

分別應用預先數據處理訓練所得的神經網絡,進行繪圖,根據插值曲線繪圖對比,選用19神經元的最大相對誤差0.028 9的神經網絡,其回歸曲線如圖5所示,可見回歸直線與理想回歸直線幾乎重合,而通過對最大的相對誤差的樣本分析發現,相對誤差大的都是○k取值最大或最小的樣本,這與系列60圖譜是一致的,因此在實際應用范圍內是有更高計算精度的,可以滿足船舶設計的需要.

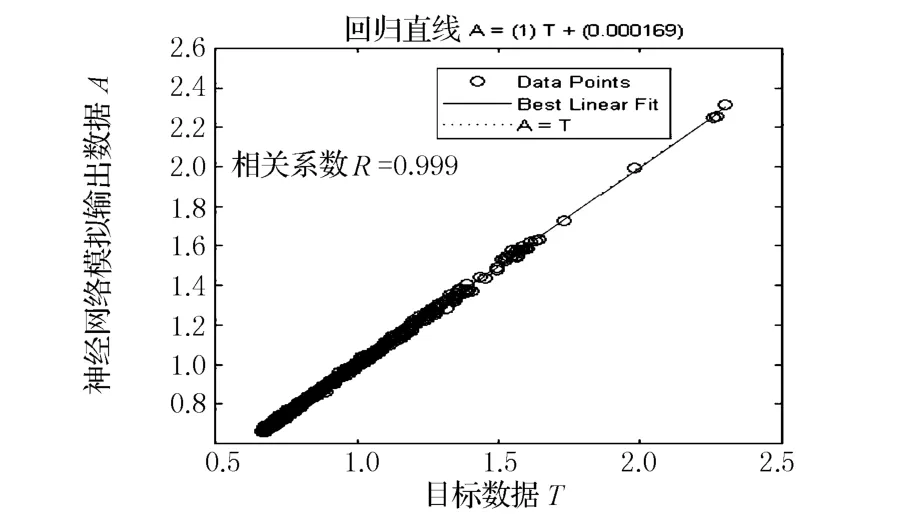
圖5 隱層19神經元最佳網絡回歸曲線

由于,訓練和檢驗樣本都是用的原始實驗數據,對B/H僅有2.5,3.0,3.5 3個數值,為驗證該神經網絡的泛化能力,對相同的Cb,L/B和○k,在B/H為2.5,3.0,3.5的數值之間進行線性插值,添加了B/H為2.66,2.84,3.16,3.34四組數值,插值后數據樣本由838組擴充到1 869組,對該神經網絡進行模擬,得到最大相對誤差為0.031 63,平均相對誤差為:0.007 246,輸出和目標的回歸直線為A=(1.000 3)T+(-0.001 513 4),可見其泛化能力是很好的.

3 船舶阻力BP神經網絡的應用

3.1 計算船舶阻力的應用

該船舶阻力神經網絡可以方便快速地計算弗氏阻力系數,如任意輸入方形系數Cb=0.70,船長型寬比L/B=7.8,型寬吃水比B/H=3.0,弗氏速率系數=1.4,對網絡進行模擬得到對應的輸出弗氏阻力系數=0.696 1.經在圖譜上查閱,其值接近0.7,與其結果一致.但顯然對于圖譜不能直接查找的數值,應用該船舶阻力神經網絡更方便.

3.2 船船阻力性能研究及船型優化的應用

顯然通過該神經網絡能很方便地作出各種阻力變化曲線,可用于分析阻力隨船型參數的變化情況.例如,在系列60船模實驗中,由于對相同的一組Cb,B/H船長型寬比L/B只有3個變化的數值,弗氏阻力系數與L/B的變化關系不能很清楚地表達出來,但通過該19隱層神經元的船舶阻力神經網絡,則可以方便地繪制其變化曲線,如B/H=2.5,=1.7,在不同 C b時,弗氏阻力系數船長型寬比L/B的變化曲線如圖6所示,從該圖可以清楚地分析出系列60船舶最低剩余阻力時的最佳L/B,及該最佳L/B隨C b的增大而變小的情況.用該神經網絡繪制的其他性能曲線如圖7所示,顯然該神經網絡拓展了系列60的應用范圍,并可應用于一定約束條件下的船型優化.

3.3 在船機槳匹配優化設計上的應用

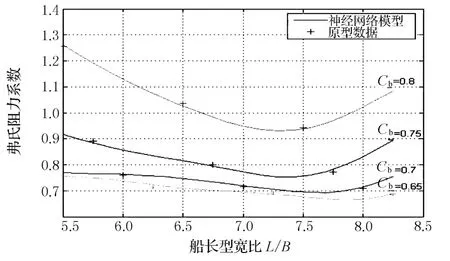
圖6 隱層19神經元網絡與L/B的變化曲線

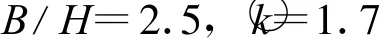
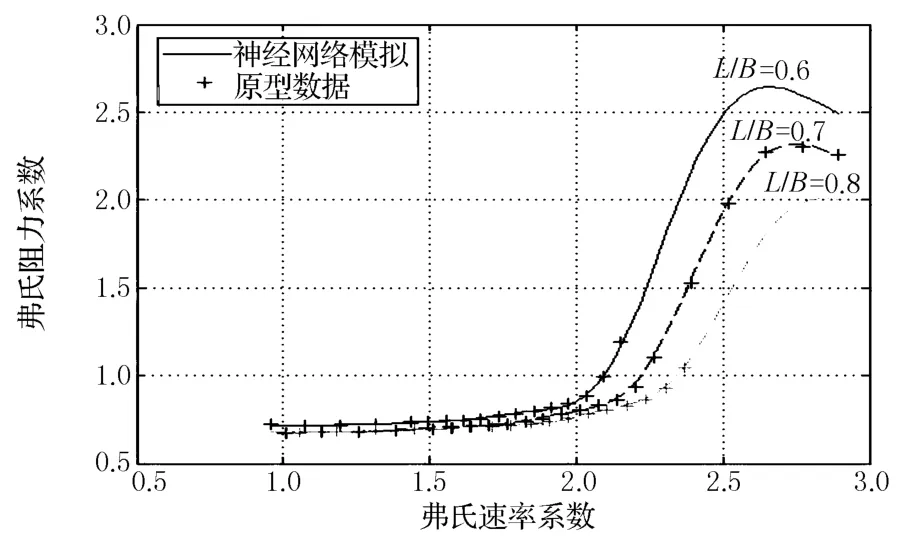
圖7 隱層19神經元網絡繪制的對○k和L/B的變化曲線

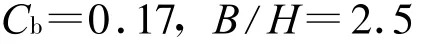
船機槳匹配優化設計時,不論是在初步匹配設計中,還是最終匹配設計中,都要計算船舶阻力,作出船舶有效功率隨航速的變化曲線,該船舶阻力神經網絡系統的研制為船機槳匹配優化設計的計算機化、智能化提供了重要的支撐.

4 結 論

1)利用船模原始實驗數據通過預先數據處理的方式,采用tansig和purelin傳遞函數,以及trainbr訓練函數和合適的隱層神經元數,可以訓練出高精度的船舶阻力計算BP神經網絡系統.

2)該神經網絡系統在船舶阻力計算研究、船型優化和船機槳優化匹配設計上比傳統方法具有無可比擬的優勢.

3)基于神經網絡能以任意精度逼近任何非線性函數的能力,抽象出更有代表性的船型參數、選用合適的速度參數,利用不同的船模系列數據,甚至是高速艦船的阻力數據,設計出具有廣泛適應性的船舶阻力計算神經網絡系統也將是現實可行的.

[1] Lippmamm R P.Introduction of Computing with Neural Nets[J].IEEE ASSP M agazine,1987,4:4-22.

[2]Funahashi K I.On the approximate realization o f continuous mappings by neura l netw orks[J].Neural Networks,1989,2(3):183-192.

[3]林 盾,陳 俐.BP神經網絡在模擬非線性系統輸出中的應用[J].武漢理工大學學報:交通科學與工程版,2003,27(5):120-123.

[4]Chen Aiguo,Ye Jiaw e.Research on the genetic neural netw ork for the computation of ship resistance[C].2009 International Conference on Computation Intelligence and Natural Computing.Wuhan,China,2009.

[5]Chen Aiguo,Ye Jiawe.Research on four layer back propagation neural netw ork for the computation of ship resistance[C].2009 IEEE International Con ference on M echatronics and Automation.Changchun,China,2009.

[6]Zhang Ling,Zhang Xianda.M IMO channel estimation and equalization using three-layer neural networks w ith feedback[J].Tsinghua Science And Technology.2007,12(6):16-19.