考慮共因失效的多態系統可靠性優化

李春洋 陳 循 易曉山

國防科學技術大學,長沙,410073

0 引言

常規系統可靠性分析中有兩個基本假設:①系統或單元只有“正常工作”和“完全失效”兩種狀態;②各單元的失效是相互獨立的。這樣的假設確實能夠為解決實際問題帶來很大的方便,但是這些假設又使得問題過于簡單,并不能真實地反映實際情況。首先,很多系統不僅有“正常工作”和“完全失效”兩種狀態,在兩者之間還存在很多種工作狀態,即系統是多態的[1,2];其次,系統中各單元的失效有時并不是相互獨立的,特別是一些大型、復雜的機電系統,相關失效是一個普遍的特征。如果忽略系統失效的相關性,簡單地在系統各單元失效相互獨立的假設下進行系統可靠性分析與計算,常常會導致過大誤差[3]。共因失效是相關失效中一種十分廣泛的形式,它是由于某種共同的原因導致多個單元同時失效,共因失效對利用單元冗余提高系統可靠性的方法有很大影響。

目前,國外學者對多態系統可靠性優化做了不少研究工作。文獻[4-5]研究了多態串—并聯系統的可靠性冗余配置優化問題,并分析了在可用度的約束下,針對資源需求固定情況,使系統費用最少的問題。文獻[6]研究了考慮維修策略的多態系統可靠性冗余配置優化問題。文獻[7]利用物理規劃方法和遺傳算法解決了多態系統可靠性冗余配置多目標優化問題。但這些文獻中的優化模型都是建立在多態系統各單元失效相互獨立的基礎上,而對于考慮共因失效的多態系統可靠性優化沒有研究。雖然文獻[8-9]研究了考慮共因失效的可靠性優化問題,但所分析的系統都是常規系統可靠性中的二態系統,并不是多態系統。文獻[10]對考慮共因失效的多態系統可靠性進行了分析,但對于在多態系統設計階段時如何進行可靠性優化設計沒有分析。本文在以上文獻的基礎上,將共因失效分析和多態系統可靠性優化相結合,分析考慮共因失效的多態系統可靠性冗余配置優化問題,并利用遺傳算法對考慮共因失效的多態系統可靠性優化問題進行求解。

1 優化模型

圖1所示的多態串—并聯系統含有n個子系統,每個子系統i由mi種可供選擇的單元并聯組成。定義每種類型單元的性能為gij,可靠度為Rij,價格為cij,子系統i的單元冗余數量為ri,系統的費用為C,可靠度為R,假設子系統i由于受環境因素影響,形成共因失效組。

根據可供選擇的單元,研究在滿足一定約束條件下,通過確定最優的單元類型和最優的冗余數量,使系統費用最少或者可靠度最大的問題就是可靠性冗余配置優化問題。對于圖1所示的系統,以可靠度為約束條件,以費用最少為目標,建立優化模型:

式中,R0為系統允許的最小可靠度;Ni為子系統i允許的最大冗余數量,i=1,2,…,n;j=1,2,…,mi。

要解決該問題,首先需要計算系統可靠度R,然后采用優化算法對優化模型進行求解。由于該優化問題是一個NP—hard問題,采用傳統的優化算法難以求解,文本采用遺傳算法進行求解。

2 多態系統可靠度計算

分析之前,做如下假設:①系統和單元不可修;②各子系統內的單元完全相同,且只有正常工作和完全失效兩種狀態;③不同的單元失效會引起系統呈現多種狀態,即系統是多態系統。

2.1 失效獨立的多態系統可靠度計算方法

多態系統可靠度計算有結構函數法、馬爾科夫過程、蒙特卡羅仿真和通用生成函數(universal generating function)四種方法。通用生成函數是解決多態系統可靠度計算問題應用較好的方法,它能夠明確地表達單元狀態概率、性能與系統狀態概率和性能的關系,并且可以通過簡單的運算由單元的通用生成函數得到系統的通用生成函數,它具有計算速度快,適用范圍廣等特點,這在多態系統可靠性優化分析中很有優勢,所以通用生成函數在多態系統可靠性優化中應用廣泛[1]。

設單元有M種狀態,單元的性能和對應的狀態概率分別為{g1,g2,…,gM}、{q1,q2,…,qM},其中ql=Pr{G=gl},G為單元的性能參數,l=1,2,…,M。則單元的通用生成函數(U函數)為

U函數將單元的狀態和單元處于這些狀態時的概率聯系了起來,利用各單元的U函數,采取復合運算就可以得到系統的U函數:

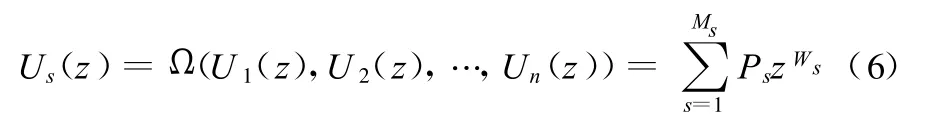
式中,s為系統狀態,s=1,2,…,M;Ms為系統的狀態數;Ps為系統狀態為s時的狀態概率;Ws為系統狀態為s時的系統性能。

系統的U函數表示系統的狀態分布和系統處于各狀態時的概率,如果系統需求是系統性能不低于w,則可以得到系統的可靠度為

根據假設條件(2),即單元只有正常工作和完全失效兩種狀態,則gij={gij,0},Rij={Rij,1—Rij},代入式(5),得單元的U函數為

若子系統的工作任務由各并聯單元共同分擔,則子系統i的U函數為

系統的U函數通過復合運算式(6)即可得到。

2.2 考慮共因失效的多態系統可靠度計算方法

考慮共因失效時,需要對上面的計算過程進行改進,分以下兩種情況[10]:

(1)發生共因失效時,共因失效組中所有單元全部失效。對于只存在單元獨立失效和共因失效組全部失效兩種失效形式的情況(如在爆炸和沖擊的作用下,單元全部失效),共因失效組子系統的通用生成函數為

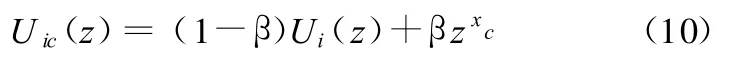
式中,Ui(z)為單元獨立失效時,共因失效組的U函數;β為共因失效的發生概率;xc為共因失效組發生共因失效時,共因失效組的輸出性能。

將Uic(z)與其他非共因失效組子系統的U函數通過復合運算式(6)進行計算,即可得系統U函數。

(2)全面考慮共因失效組各重共因失效。此時,在U函數中加入指針矢量,將U函數式(5)改進為V函數:

式中,sl為指針矢量,維數為n,用于表示該單元是否屬于共因失效組,以及屬于哪個共因失效組。

在計算系統的V函數過程中,屬于共因失效組的單元的狀態概率ql用1代替,非共因失效組的單元的狀態概率不予置換。通過類似U函數的復合運算,得到系統的V函數如下:

最后,將系統的V函數轉化為U函數,通過下式實現:

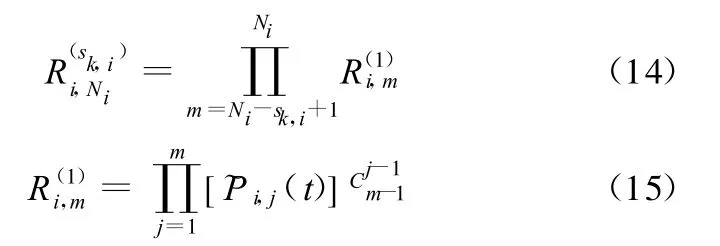
式中,~Pi,j(t)為共因失效組i中j重共因失效不發生的概率。

3 利用遺傳算法求解優化模型

遺傳算法求解優化模型式(1)～式(4)的相關流程和設置如下[12]:

(1)編碼。本文采用實數編碼,定義每個染色體的形式為vk=(bk1,bk2,…,bkn,rk1,rk2,…,rkn),其中,bki表示子系統i選擇的單元類型,rki表示選擇單元的冗余數量,兩者都為整數。

(2)產生初始群體。定義種群規模為pop_size,并隨機產生pop_size個染色體,其中,染色體的每個基因位在其取值范圍內隨機取值,取值范圍為1≤bki≤mi,1≤rki≤Ni。

(3)計算適應值。首先計算每個染色體所對應的系統費用Ck和系統可靠度Rk,對于不滿足約束條件的染色體,定義如下的懲罰函數:

如果滿足約束條件式(2),則適應值為 fk=Ck,不予懲罰;如果不滿足約束條件式(2),給予懲罰,則適應值為 fk=Ck+K(R0—Rk),其中K是一個很大的正數。定義懲罰函數的目的是將優化算法引導到臨近的最優可行解上,逐漸淘汰不可行解。

(4)選擇。首先對適應值進行正規化標定:

式中,fmax和fmin分別為種群中最好和最壞的適應值;γ為很小的正實數,以防止分母為零。

對適應值進行正規化標定之后,采用賭輪盤法選擇染色體進行交叉。

(5)交叉。對父代采用單點交叉以產生子代。定義交叉概率為Pc,選擇兩個父代,隨機產生一個交叉點,交換兩個父代染色體交叉點后的基因位,從而產生兩個子代。

(6)變異。采用隨機攝動進行變異。定義變異概率為Pm,在種群所有染色體的基因位中產生[0,1]之間的隨機數,所有小于Pm的隨機數所對應的基因位作為變異的基因位。對于一個選取變異的基因位Ji,用該基因位取值范圍內的一個隨機整數進行替代。

(7)產生新一代種群。為了避免最優的染色體經過交叉、變異之后,產生適應值較小的染色體,將當前群體中最優的部分染色體保留到下一代,和變異之后的染色體一起組成新一代種群。

(8)終止。遺傳算法是一個反復迭代的過程,每一次迭代都要執行適應值計算、選擇、交叉、變異等操作,直到滿足終止條件。終止條件可以是規定的最大迭代代數或規定的最小偏差。

由于遺傳算法的優化結果與初始種群的選擇有關系,不同的初始種群可能會收斂于不同的局部最優解,而不是全局最優解。為了解決該問題,本文首先循環運算遺傳算法pop_size次,計算出pop_size個解,然后將所得到的pop_size個解作為新的初始種群,再利用遺傳算法求解,從而得到最終解,這樣可以防止收斂于局部最優解。當然,這樣處理時計算時間相對較長,可以通過調整種群規模pop_size和迭代代數來控制計算時間。

4 算例分析

分析文獻[4]中的電力供煤系統,由主進料器和傳送帶子系統、堆垛運輸機和次進料器子系統、卸料器子系統、鍋爐子系統這4個部分串聯而成,每個子系統由市場上可供選擇的單元并聯組成,每個子系統只能選擇一種類型的單元。每種類型的單元有其對應的性能、可靠度和價格,如表1所示。要求系統的輸出性能水平不小于0.8,并且系統可靠度不小于0.9,以市場上可供選擇的單元進行合理搭配,實現費用最少的目標。

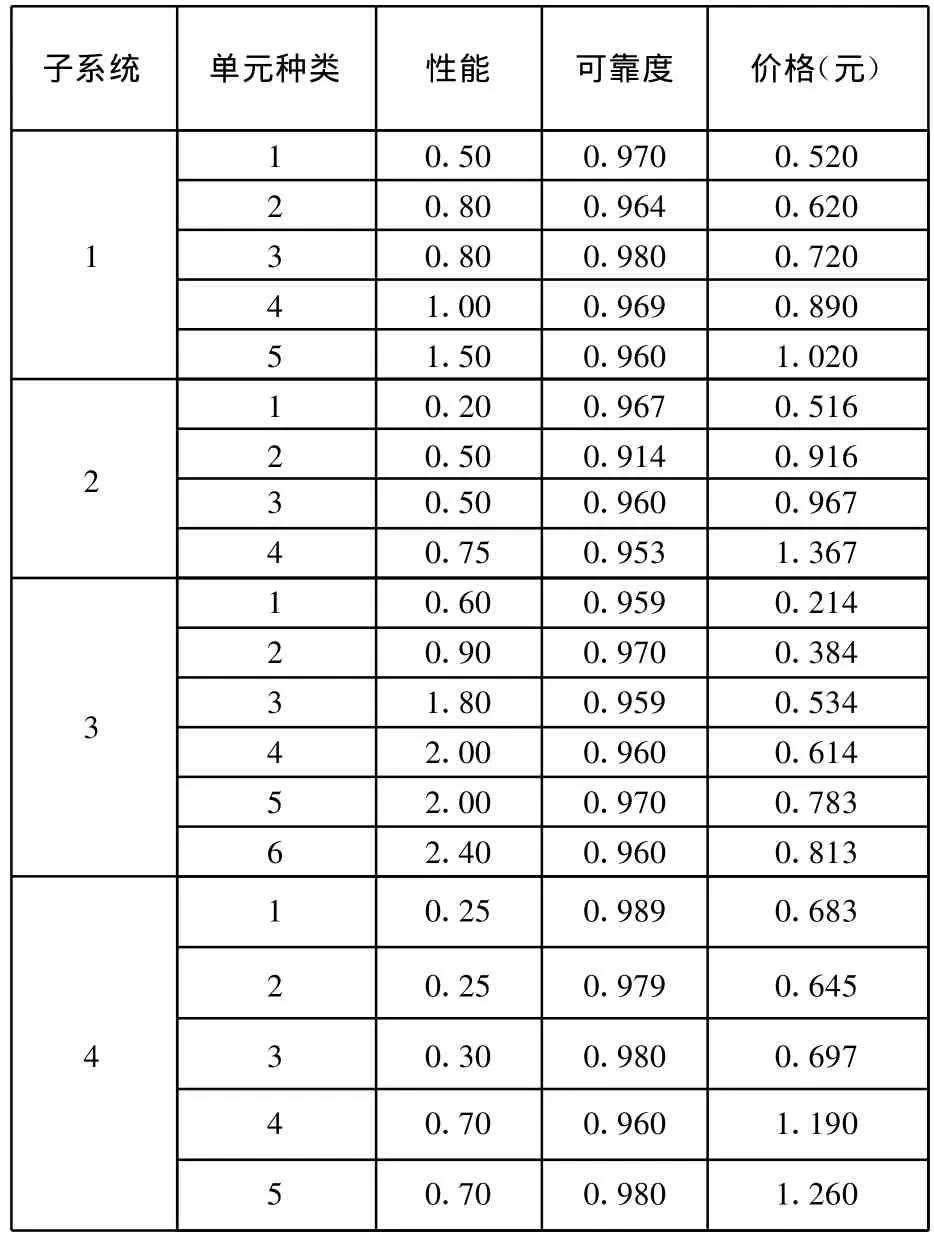
表1 可供選擇單元的相關參數

假設各子系統允許的最大冗余數量為5,則可以建立如下的優化模型:

令種群規模pop_size=20,懲罰函數的系數K=100,正規化標定函數的參數γ=0.001,交叉概率Pc=0.8,變異概率Pm=0.02,終止條件為規定的迭代代數500。根據失效形式,分以下三種狀況進行分析:

(1)不考慮共因失效。

(2)發生共因失效時,共因失效組中所有單元全部失效。假設子系統1、3會發生共因失效,發生共因失效的概率分別為0.010和0.015,發生共因失效時子系統1、3的所有單元均失效。

(3)全面考慮共因失效組各重共因失效。假設子系統1、3發生共因失效,發生各重共因失效的概率與所選擇的單元有關,發生2重共因失效的概率為單元獨立失效概率的1/2,發生3重共因失效的概率為 2重共因失效概率的1/2,依此類推。

三種狀況的優化結果對比情況如表2所示。

表2 三種狀況的優化結果對比

從三種狀況的優化結果可以看出,在不同條件下,優化的結果相差很大。將不考慮共因失效的優化結果,分別代入考慮共因失效的狀況2和狀況3,可靠度為0.8859和0.8450,是不滿足可靠度不小于0.9的約束條件的。這說明在考慮共因失效時,為了提高系統的可靠度,單純地使用冗余已經不是一個很好的辦法,而使用較高可靠度的單元有更好的效果。上面的分析中,考慮各重共因失效時,子系統3選擇單元2而不選擇獨立失效時選擇的單元1就是一個很好的說明。

5 結論

(1)本文利用遺傳算法對考慮共因失效的多態系統可靠性優化問題進行了分析和求解,并且與不考慮共因失效的多態系統可靠性優化結果進行了對比。對比顯示,兩者的優化結果有較大的差別。由于共因失效削弱了冗余的效果,使得在進行可靠性優化設計時,對于易于發生共因失效的系統,需要采取與獨立失效系統不同的可靠性設計方案,即不能簡單地利用冗余設計提高系統可靠性,而應該根據費用情況選擇更加可靠的單元。

(2)本文在分析中,假設單元只有兩種狀態,而且是不可修的,以后的研究可以進一步深入。

[1]Levitin G.The Universal Generating Function in Reliability Analysis and Optimization[M].London:Springer,2005.

[2]Lisnianski A,Levitin G.Multi—state System Reliability:Assessment,Optimization and Applications[M].Singapore:World Scientific,2003.

[3]李翠玲,謝里陽,李劍.基于零件條件失效概率分布的共因失效模型[J].中國機械工程,2006,17(7):753-757.

[4]Levitin G,Lisnianski A,Ben—haim H,et al.Redundancy Optimization for Series—parallel Multi—state Systems[J].IEEE Transactions on Reliability,1998,47(2):165-172.

[5]Levitin G.Redundancy Optimization for Multi—state System with Fixed Resource—requirements and Unreliable Sources[J].IEEE Transactions on Reliability,2001,50(1):52-59.

[6]Nourelfath M,Ait—kadi D.Optimization of Series—parallel Multi—state Systems under Maintenance Policies[J].ReliabilityEngineeringand System Safety,2007,92:1620-1626.

[7]Tian Zhigang,Zuo M J.Redundancy Allocation for Multi—state Systems Using Physical Programming and Genetic Algorithms[J].Reliability Engineering and System Safety,2006,91:1049-1056.

[8]Bai D S,Yun W Y,Chung S W.Redundancy Optimization of k—out—of—n Systems with Common —cause Failures[J].IEEE T ransactions on Reliability,1991,40(1):56-59.

[9]Ramirez—Marquez J E,Coit D W.Optimization of System Reliability in the Presence of Common Cause Failures[J].ReliabilityEngineeringand System Safety,2007,92:1421-1434.

[10]Levitin G.Incorporating Common—cause Failures into Nonrepairable Multistate Series—parallel System Analysis[J].IEEE Transactions on Reliability,2001,50(4):380-388.

[11]Chae K C,Clark G M.System Reliability in the Presence of Common—cause Failures[J].IEEE Transactions on Reliability,1986,35:32-35.

[12]玄光男,程潤偉.遺傳算法與工程優化[M].北京:清華大學出版社,2004.