基于粒子群算法和分割逼近法的復雜曲面輪廓度誤差計算

廖 平

中南大學,長沙,4100831

0 引言

復雜曲面在現代機械制造業中的應用越來越廣泛,在工程實際中,針對復雜曲面的高效率、高精度的測量要求也越來越高。最小區域法是我國和ISO評定復雜曲面輪廓度誤差的標準。但是,復雜曲面輪廓度誤差的求解是一個復雜非線性尋優問題[1-5],目前采用的大多是傳統的近似求解方法,因此,基于最小區域法的復雜曲面輪廓度誤差的計算仍然是一個難題。

美國學者Kennedy等[6]于1995年提出了粒子群優化(particle swarm optimization)算法,該算法具有高效并行優化、流程簡單、不需要梯度信息、容易實現等特點,對求解復雜曲面輪廓度誤差非線性優化問題具有獨到之處。

本文提出了基于粒子群算法和分割逼近法的復雜曲面輪廓度誤差的計算方法。

1 粒子群優化算法的基本原理

粒子群優化算法是一種基于群智能方法的演化計算技術,其思想來源于對鳥群捕食行為的模擬[6-7],采用速度—位置搜索模型,在優化問題的D維空間隨機產生一個粒子數為m的初始種群,并賦予每個粒子一個隨機速度。更新粒子的速度和位置可表示為

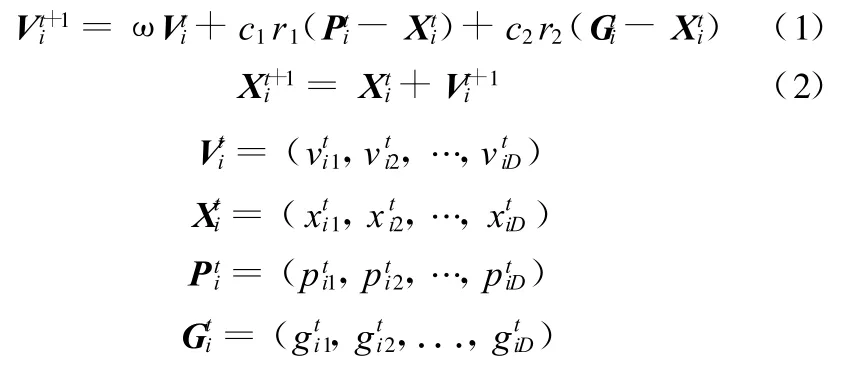
式中,Vti為粒子i第t次迭代速度矢量;ω為慣性因子,ω≥0;c1、c2為學習因子;r1、r2為均勻分布在(0,1)區間的隨機數;Xti為粒子i第t次迭代位置矢量;Pti為粒子最好位置;Gti為種群當前最好位置。

假設求函數f(X)的最小值,那么粒子i的個體最優位置為

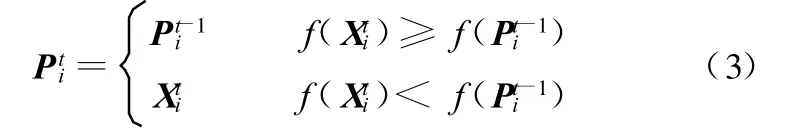
則群體粒子的領域最優值和對應的位置為

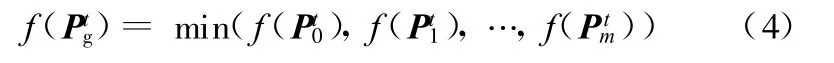
2 復雜曲面NURBS描述及其輪廓度誤差的定義

2.1 基于NURBS描述復雜曲面

在CAD/CAM/CAGD中,形狀復雜、不規則的曲線輪廓一般以一組離散坐標點和相應控制參數表示,坐標測量機對輪廓進行測量時得到的也是一組離散坐標點。對于這些離散的坐標點一般用參數樣條曲面進行擬合。而NURBS曲面具有局部性、變差縮減性、凸包性、在仿射與透視變換下的不變性、參數連續性,以及權因子的調形性等一系列優良性能,在航空、航天、造船、汽車及模具工業的計算機輔助設計和輔助制造過程中得到廣泛應用。一個k次NURBS曲面可以表示為多片有理多項式矢函數形式[8]:

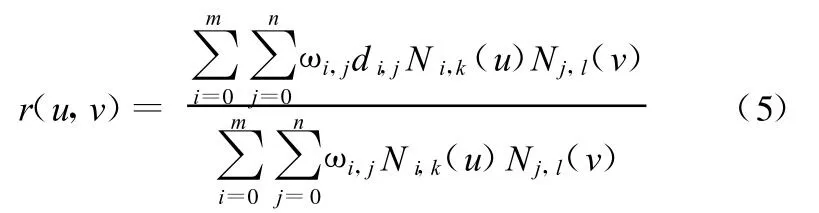
式中,di,j為矩形域上特征網格控制點;ωi,j為相應控制點的權因子,規定四角點處用正權因子,即 ω0,0,ωm,0,ω0,n,ωm,n ＞0,其余 ωi,j≥0;Ni,k(u)、Nj,l(v)分別為u向k次和v向l次規范B樣條基函數,它們分別由節點矢量U=(u0,u1,…,um+k+1)與V=(v0,v1,…,vn+l+1)由De Boor—Cox遞推公式決定。

2.2 復雜曲面輪廓度誤差的定義

按最小區域法來評定復雜曲面輪廓度誤差,其誤差值是包容被測輪廓的兩理論輪廓等距面的最小距離,如圖1所示。

設復雜曲面理論基準點為(xtb,ytb,ztb),實際輪廓測得基準點為(xb,yb,zb),輪廓測點坐標為P={Pj=(xj,yj,zj)|j=1,2,…,m},其坐標變換矩陣為

式中,Tp為測點平移坐標變換矩陣;Tx為測點繞x軸旋轉θ后的變換矩陣;Ty為測點繞y軸旋轉φ后的變換矩陣;Tz為測點繞z軸旋轉ψ后的變換矩陣。

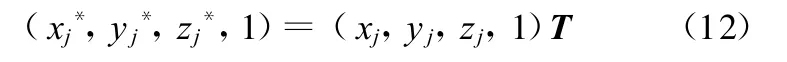
測點變換后的新坐標為復雜曲面輪廓度誤差數學模型為

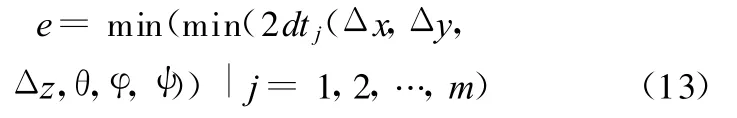
式中,dtj(Δx,Δy,Δz,θ,φ,ψ)為測點(xj,yj,zj)經過坐標變換后到理論輪廓的最小距離。

從復雜曲面輪廓度誤差數學模型理論可知:只有測點的位置位于最佳位置時,才能保證包容全部測點的理論輪廓等距面之間的距離最小,這是一個非常復雜的非線性優化問題[9-10]。

3 用分割逼近法計算測點到設計曲面輪廓的最小距離

設測點坐標為(xk,yk,zk),如圖2所示,該點到用NURBS曲面描述的理論輪廓r(u,v)最小距離的數學模型為

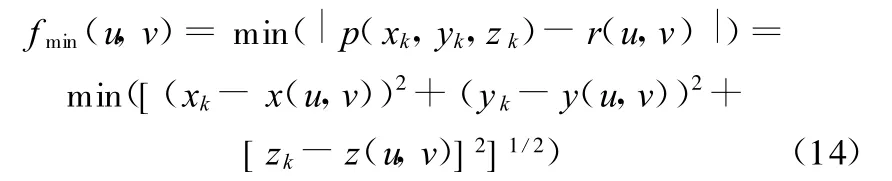
要精確計算點到復雜曲面的最小距離,需要解決求解方法的選擇和算法的計算效率兩個關鍵問題。采用微分幾何方法求測點到理想輪廓的最小距離計算方法復雜,且工作量大,為此,本文提出一種快速數值求解法 ——分割逼近法。

(1)將NURBS曲面r(u,v)u向10等分、v向10等分,在曲面上形成11×11網格點r(ui,vj)(i=0,1,…,10;j=0,1,…,10)。

(2)計算測點 pk到理論曲面網格點r(ui,vj)(i=0,1,…,10;j=0,1,…,10)上的距離dts

i,j,初始分割時取s=1。如圖 3所示。

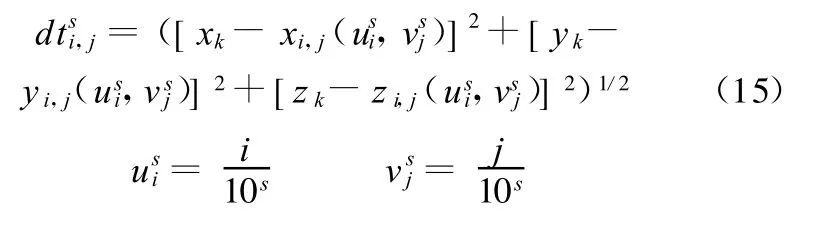
(3)求測點到理論曲面上所有網格點距離的最小值:

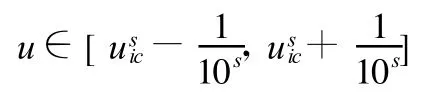
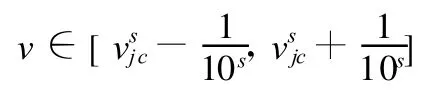
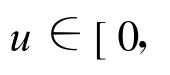
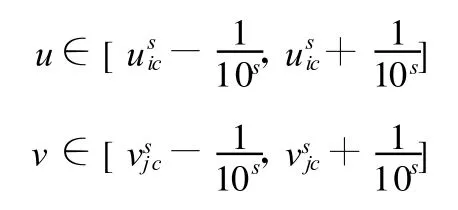
繼續分割10×10等分,在曲面上形成11×11網格點r(us+1i,vs+1j)(i=0,1,…,10;j=0,1,…,10),轉到(2),繼續求解。

4 粒子群算法和分割逼近法相結合計算復雜曲面輪廓度誤差

(1)基本參數設置。c1=2,c2=2,ω=1,粒子群數量為n=30,最大迭代次數為tmax=100。

(2)粒子群初始化。在參數(Δx,Δy,Δz,θ,φ,ψ)允許的范圍內隨機初始化粒子群體的位置:

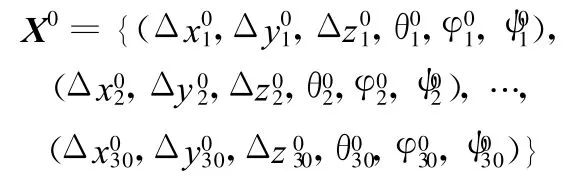
隨機初始化對應的速度:

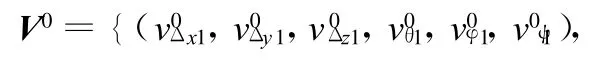
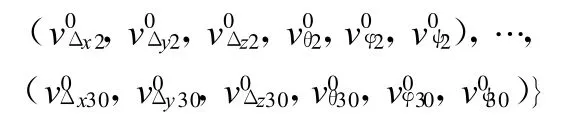
每個粒子的初始最優與初值相同,即

由式(4)求初始種群到達的最優位置,即

(3)確定適應值函數。選取復雜曲面輪廓度誤差的目標函數為適應值函數,即個體(Δxti,Δyti,Δzti,θti,φti,ψti)所對應的各測點到理論設計輪廓的最小距離中的最大值為

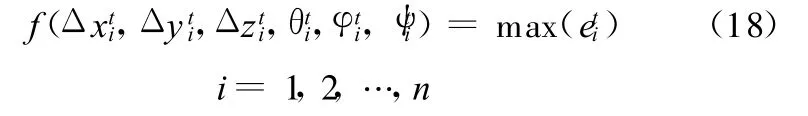
其中,eti為所有測點P={(xj,yj,zj)|j=1,2,…,m}經過(Δxti,Δyti,Δzti,θti,φti,ψti)所對應的坐標變換后到理論設計輪廓的最小距離,eti采用分割逼近法求得。

(4)求出每一個粒子的最優位置。首先計算每個粒子的適應值 f(Δxti,Δyti,Δzti,θti,φti,ψti),然后求出每一個粒子的最優位置:

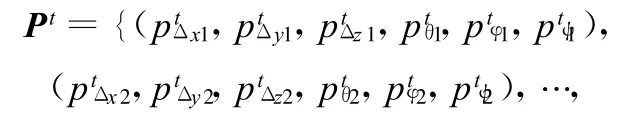
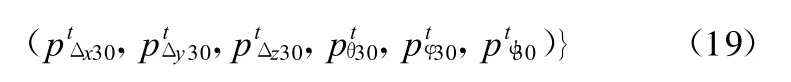
(5)求當代種群中到達的最優位置,即

(6)根據式(1)、式(2)更新每個粒子的位置和飛行速度。

(7)檢查更新粒子位置越限情況并進行相應處理。

(8)判斷迭代次數t是否到達設定值tmax,如未達到則繼續迭代;若達到則停止計算,此時得到的種群中最優位置為Ptg,所對應的適應值即為復雜曲面輪廓度誤差。

5 計算實例

表1為一理論設計輪廓三次NURBS曲面特征頂點,表2為實際輪廓測點,其中:

U=(0,0,0,0,0.5,1,1,1,1)

V=(0,0,0,0,0.5,1,1,1,1)

采用粒子群算法和分割逼近法相結合方法計算得到的輪廓度誤差為0.073 788 109 106 757 8mm,采用最小二乘法計算的輪廓度誤差為0.095 179 980 162 99 9mm,從計算結果可以看出采用粒子群算法和分割逼近法相結合的方法計算輪廓誤差值比最小二乘法的計算結果小,說明最小二乘法獲得的不是最優解,不符合最小區域法評定復雜曲面輪廓度誤差的標準。

表1 理論輪廓控制點坐標 mm

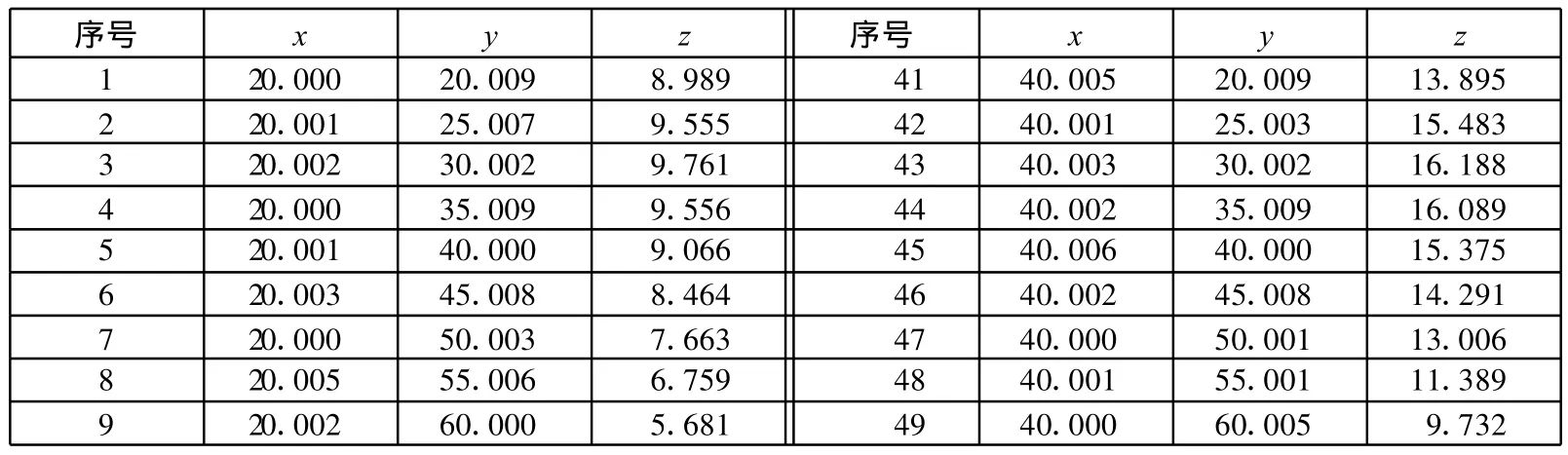
表2 測點坐標 mm

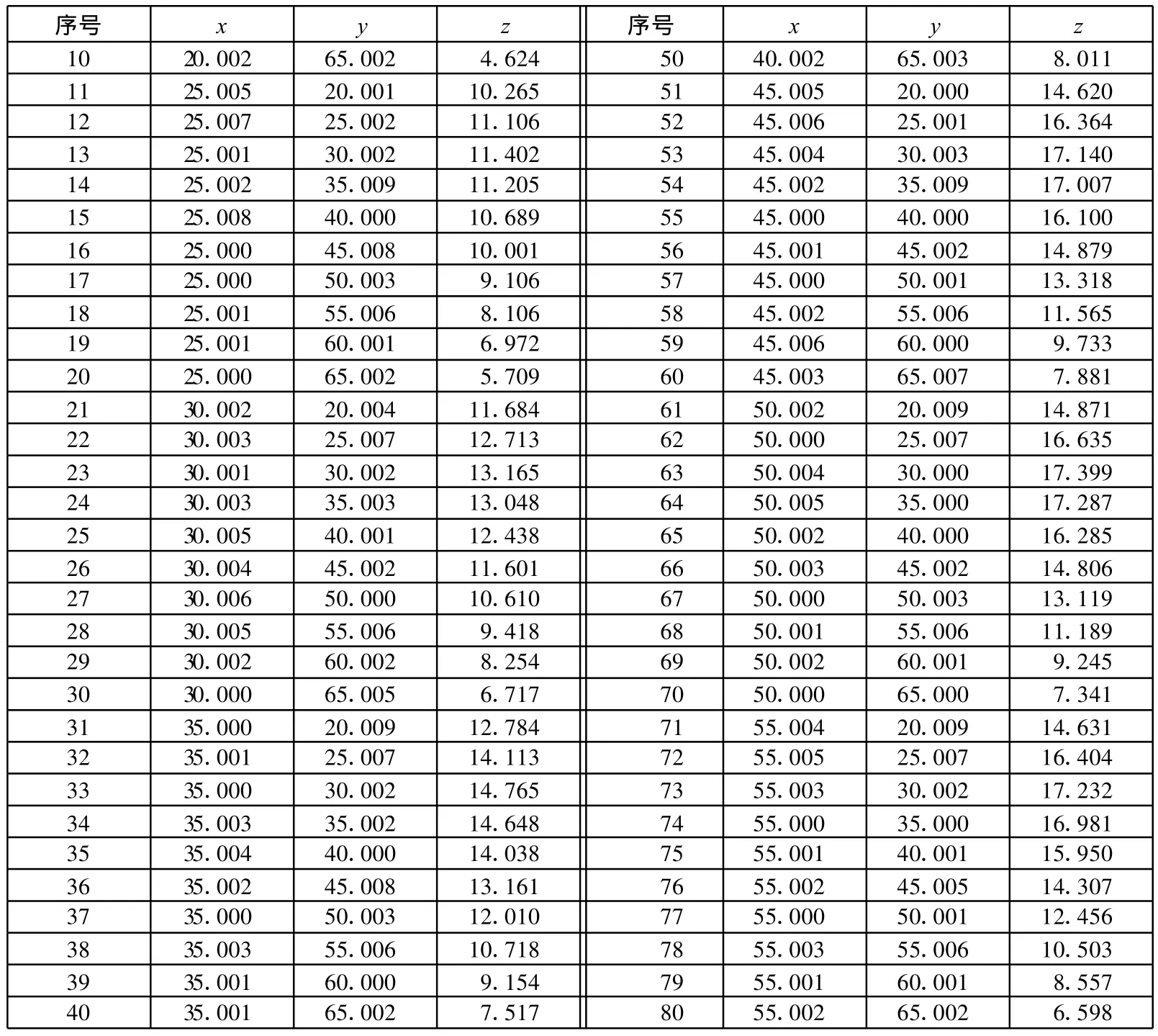
(續表)

6 結束語

本文采用粒子群算法和分割逼近法相結合的方法計算復雜曲面輪廓度誤差,其精確度非常高,可達到任意給定的精度值,理論上可以收斂于全局最優解,完全符合最小區域法的評定標準。該算法簡單明了,易于計算機程序實現,為復雜曲面輪廓度誤差的數據處理開辟了新的途徑,尤其非常適用于三坐標測量機、飛機型架三坐標測量系統的復雜曲面輪廓度誤差的測量數據處理。

[1]侯宇,張競,崔晨陽.復雜線輪廓度誤差坐標測量的數據處理方法[J].計量學報,2002,23(1):13-16.

[2]郭慧,林大鈞.基于微粒群算法的復雜曲面輪廓度誤差計算[J].東華大學學報(自然科學版),2008,34(3):274-277.

[3]王伯平,曾建潮.一種自調整的空間面輪廓度誤差的評定方法[J].計量學報,2002,23(2):106-108.

[4]Yu Yuan,Lu Jun,Wang Xiaochun.Modeling and A-nalysis of the Best Match in Free—form Surface Measuring[J].Mechanical Science and Technology,2001,20(3):19-20.

[5]Liu Yujun,Zhu Xiuli.Research on Curve Surface Fairing of Complicated Ship Hull Plate[J].Journal of Dalian University of Technology,2005,45(2):226-229.

[6]Kennedy J,Eberhart R C.Particle Swarm Optimization[C]//Proc.of IEEE International Conference on Neural Networks.Piscataway,New Jersey:IEEE Service Center,1995:1942-1948.

[7]Eberhart R C,Shi Y.Particle Swarm Optimization:Developments,Applications and Resources[C]//Proc.of Congress on Evolutionary Computation.Piscataway:IEEE Press,2001:81-86.

[8]Choi B K,Yoo W S,Lee C S.Matrix Representation for NURBS Curve and Surface[J].Computer—aided Design,1990,22(4):235-240.

[9]劉元朋,劉晶,張力寧.復雜曲面測量數據最佳匹配問題研究[J].中國機械工程,2005,16(12):1080-1082.

[10]Kyuseojin A,Akmoto Y.A New Method of Best—fitting on Curved Surface[J].SPIE,1993,2101:54-61.