基于模型預測算法的無人機延時控制系統設計＊

張 舉，祝小平，周 洲

（西北工業大學，西安 710072）

0 引言

無人機飛行有自主飛行和“人在回路中”控制兩種基本方法。自主控制面臨建立智能性、獲得安全性和成本三方面的挑戰。“人在回路中”無人機能夠克服自主飛行的不足，但“人在回路中”無人機，對于遠程超視距任務時，需通過衛星數據鏈進行對無人機和地面控制站構成閉環回路，這樣會對整個回路帶來較大的延時。

針對回路延遲補償的研究，Smith預測器通過反饋補償來消除控制回路的延時［1］，但存在滯后輸出。在飛行模擬器中，由于計算速度、傳輸距離、數據采樣等引起的延時，會引起駕駛員誘發震蕩。文獻［2］對超前／滯后補償、有限脈沖預測濾波器補償和狀態空間預測補償這三種方法進行了評述，并提出兩種新的預測器。文獻［3］用狀態預測算法補償解決延時問題。

文中采用基于參考模型預測算法對無人機狀態進行估計來彌補由于傳輸延時帶來顯示滯后問題。

1 問題描述

“人在回路中”無人機在遠距離飛行時，地面控制站與飛行中的無人機通過衛星中繼形成閉環回路。

無人機系統的傳輸延遲時間定義為從操作者發出輸入指令到該輸入在人機界面產生與之對應的輸出這一段時間。無人機系統延時，除了具有飛行模擬器延時（采樣延遲、處理延遲和數據傳輸延遲）外，還包括通過衛星傳輸數據的固有距離和網絡節點與其它設備產生的延遲。圖1展示了人在回路中無人機系統工作示意圖。對操作人員來說所有的延時都可歸結為人機界面顯示的滯后，根據界面顯示的數據圖像作為反饋。當延時超過一定的限度時，操作者將看到屏幕顯示的內容達不到他所期望的狀態，因此他的直覺將進一步操縱指令直到顯示期望的水準，但是由于時間延遲，導致對系統過度控制，進而進一步補償和修改，這樣的往返重復過程引起駕駛員震蕩。由于駕駛員的誘發震蕩使人機系統的性能惡化，進而增加操作人員的工作負擔，甚至使系統不能正常工作。為了減小延時對無人機系統的影響，就需要對延時系統進行補償。

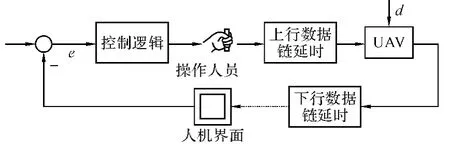
圖1 “人在回路中”無人機系統控制示意圖

2 基于模型的狀態預測延遲補償

延時在頻域上表現為相位的延遲，而相位的滯后引起系統的惡化甚至使系統不穩定。對控制系統的延時補償有多種方法，共同特性是保證系統的穩定性，不考慮補償后系統相對于無延時的延遲輸出。對人在回路中的無人機系統，操作者通過地面控制站內的人 機界面觀測飛行器的狀態和外部場景，由于系統的延遲導致操作者不能實時掌握其具體情況，得到的情形為飛行器延遲前的圖像和狀態。由于延遲系統不能產生實時場景，操作人員不能實時對無人機進行控制。基于人在回路中無人機系統的特點，補償的理想狀態為根據飛行器的當前狀態信息預測未來飛行器的狀態，這樣基于預測狀態的數據顯示可以彌補系統延時。文獻［4］用狀態空間技術，對飛行模擬器的延遲進行狀態預測。下面對狀態預測補償算法進行推導：

對于完全能控、能觀測系統，線性時不變狀態方程系統為：

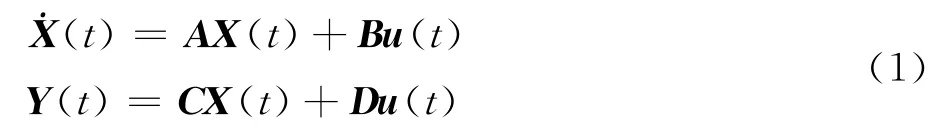
式中：X（t）∈Rn為狀態變量，Y（t）∈Rp為輸出變量，u（t）∈Rp為輸出變量。A∈Rn×n、B∈Rn×m、C∈Rp×n、D∈Rp×m為狀態方程系數矩陣。

如果給定初始條件X（t0），控制量u（t），則狀態變量X（t）對給定時間t通過式（2）來確定：

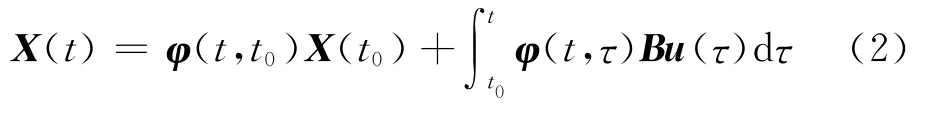
式中，φ（t，τ）＝eA（t－τ）為狀態轉移矩陣。

假如在區間［t0，t］的值選定為延遲周期td，即t＝t0＋td，那么X（t）的值為：

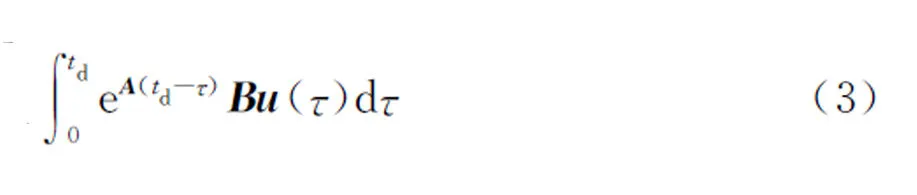
然而將來的輸入是未知的，式（3）中的卷積不能預先求出，但可以通過對輸入形式作合理的假設，如：分段常數、正弦函數、指數衰減等，這樣就可以提前計算出閉環解。這里假設在區間［t0，t0＋td］內，輸入u（τ）的值為u（t0）。圖2為狀態預測系統方框圖，Xp為預測變量。

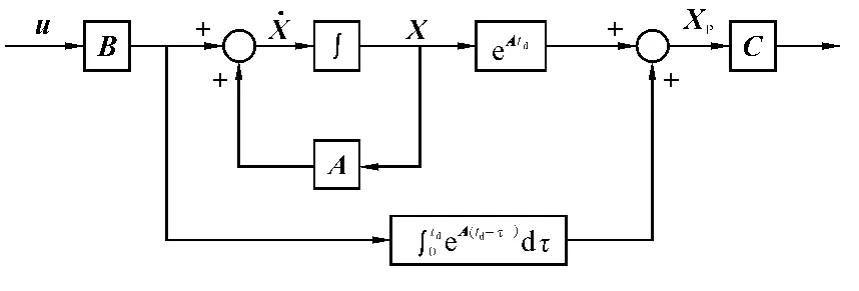
圖2 預測系統方框圖

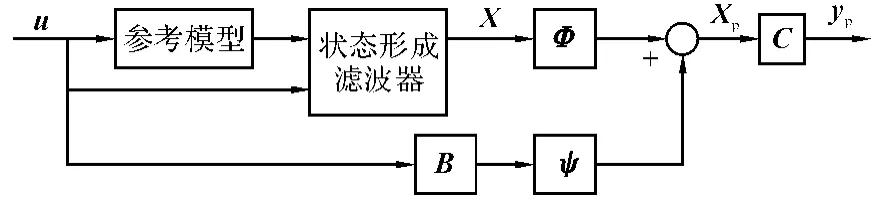
圖3 基于參考模型的狀態空間補償器結構圖

3 延遲俯仰控制回路補償設計

為了進行驗證上一節補償算法的有效性，對某飛機的俯仰角控制回路進行設計，圖4為其框圖。首先對阻尼回路（俯仰角速率回路）進行設計，確保內回路有足夠的阻尼；然后把設計好的阻尼回路作為狀態預測器的參考模型；最后選擇合適的駕駛員模型，實現俯仰角指令跟蹤。

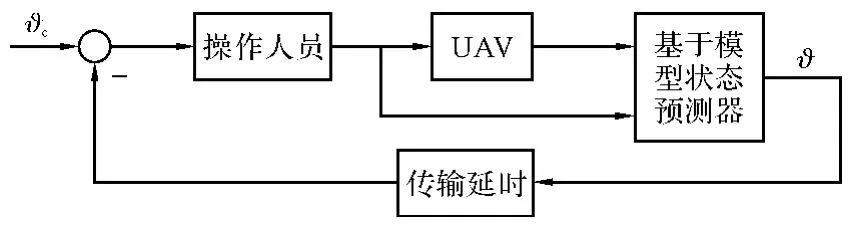
圖4 俯仰姿態控制回路方框圖

式（4）為某飛機短周期的狀態空間小擾動線性化模型，Δα為飛機迎角的變化，Δq為俯仰角速率變化，Δδe為升降舵偏角變化。

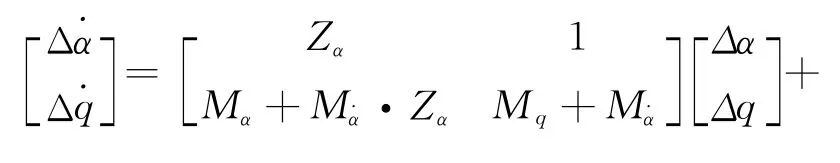
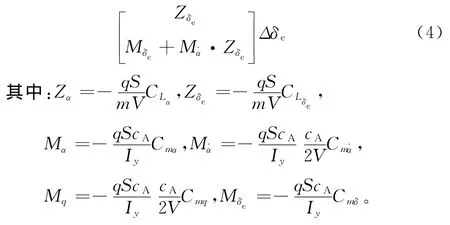
式中：q為動壓；S為飛機特征面積；cA氣動弦長；V為飛行速度。

由式（4）可求出俯仰角速率對俯仰操縱的傳遞函數為：

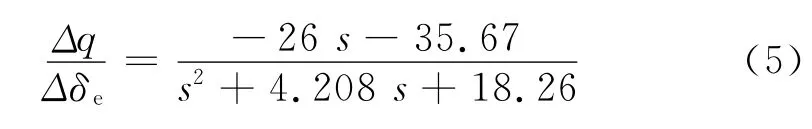
由式（5）可計算出其阻尼比為ξ＝0.49，內回路采用角速率反饋δe＝，回路的根軌跡為圖5。當阻尼比ξ＝0.707時，反饋系數為＝－0.09。

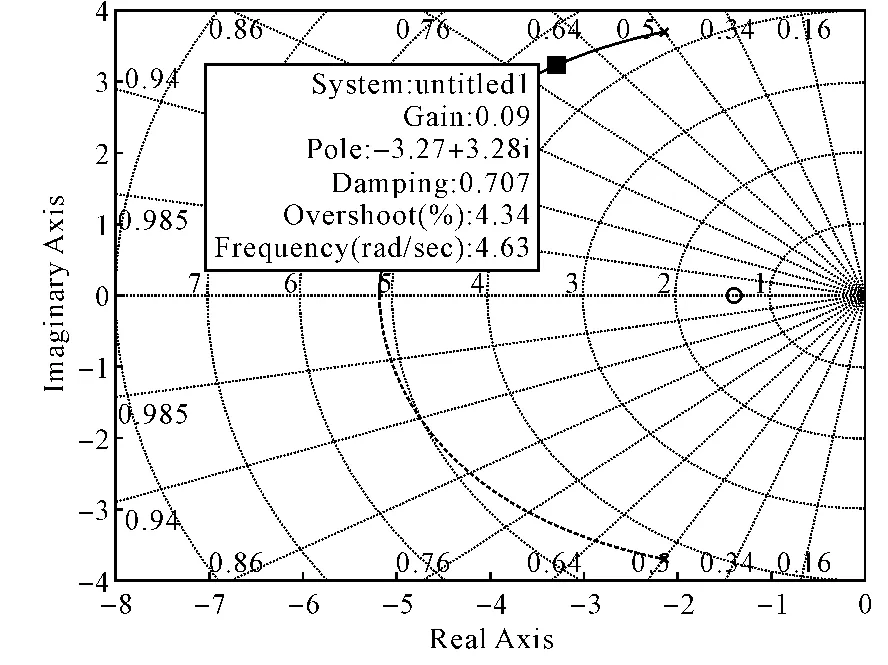
圖5 阻尼回路根軌跡圖

俯仰角速率反饋后的等效阻尼回路傳遞函數為：

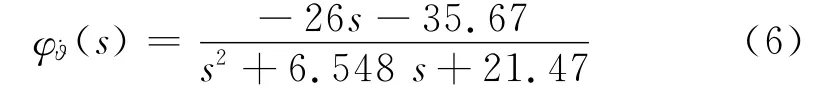
構造能觀狀態空間方程，以便求出矩陣Φ＝和狀態變量：

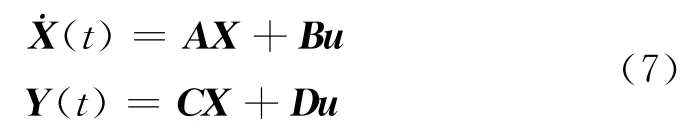
根據Neal－Smith要求，操作人員模型由可變增益Kp和可以變化的一階超前／滯后補償器和固定延遲τp組成［5］。其傳遞函數為：

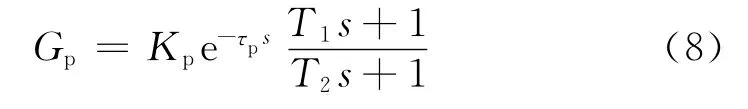
4 仿真分析

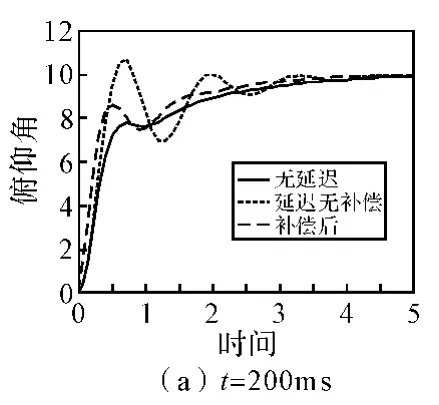
圖6 不同延遲時間下的俯仰角響應

為驗證設計的延遲無人機系統的補償算法的有效性，對俯仰角跟蹤回路進行了仿真。仿真條件：基于設計點的數據進行仿真；操作員模型假設為常值0.8；輸入信號為階躍輸入。系統分別在延遲時間為200ms、400ms和600ms的條件下進行仿真，仿真結果如圖6。由俯仰角響應可以看出補償后系統響應比不補償的性能有較大的提高，且隨延遲時間的增加愈加明顯，當延遲超過600ms時，未補償的系統變得不穩定。

5 結論

通過衛星中繼進行遠距離控制的“人在回路中”無人機系統，整個人-機控制回路存在較大傳輸延遲，延時惡化了對無人機的控制性能。基于人-機界面控制回路的特殊性，通過狀態預測補償方法來補償延時的滯后。通過采用基于參考模型的狀態預測方法來解決無人機飛行動力學的非線性、時變、耦合問題的預測，并對俯仰角控制回路進行了設計。仿真結果表明，基于模型預測補償方法減小傳輸延遲對系統的影響。

［1］Smith O J M.A controller to overcome dead time［J］.ISA Journal，1959，6（2）：28－33.

［2］Liwen Guo，Frank M Cardullo.New predictive filters for compensating the transport delay on a flight simulation，AIAA 2004－5441［R］.2004.

［3］Andrew J Thurling，Kelly A Greene.An improved predictive algorithm for time delay compensation in UAVS，AIAA 2001－4424［R］.2001.

［4］Sobiski D J，Cardullo F M.Predictive compensation of visual system time delays，AIAA－2434［R］.1987.

［5］Raman K Mehra，Ravi K Prasanth.Quantication and measurement of autonomy for UAVs using human operator modeling，AIAA 2003 6605［R］.2003.