基于可拓的Vague相似度計算

崔春生

(北京理工大學管理與經濟學院,北京 100081)

基于可拓的Vague相似度計算

崔春生

(北京理工大學管理與經濟學院,北京 100081)

在Vague的各種理論和應用中,相似度占據著不可低估的重要作用。筆者針對目前相似度的不同研究方法,通過引入點與區間“距”的概念,借助可拓關聯函數構建了一種新的相似度度量公式,進而為Vague的研究提供了一種新的思路。最后通過實例驗證了該方法的可行性。

Vague集;相似度;可拓;關聯函數

Vague集來源于Fuzzy集,在Fuzzy集基礎上,通過引入真隸屬度和假隸屬度,給出以區間形式表示的隸屬程度——該區間能夠同時給出支持證據和反對證據的程度,并且能夠表示中立的程度,從而提出Vague集的概念[1]。GAU等在1993年提出的Vague集[1]等同于A TANASSOV提出的直覺模糊集[2]是ZADEH模糊集[3]的一種推廣形式。這使得Vague集在處理不確定性信息時比傳統的模糊集有更強的表示能力。目前,Vague集已在國內外成功地運用于決策分析、專家系統、模糊控制及故障診斷等領域,并取得較傳統模糊集理論更好的效果。

Vague集(值)之間的相似度度量是Vague集理論在模糊決策、模式識別、模糊推理、機器學習、社會選擇等方面應用的理論基礎,近年來一直是學者們關注的熱點。目前,Vague集(值)相似度度量的主要依據是Vague值的真、假隸屬函數、核函數、未知度函數這4個指標,利用Vague值在這4個指標上的差異,給出度量公式[4]。從現有度量公式的表現形式及主要特點來看,主要有3種思路。

第1種是基于Vague值的記分函數,有代表性的研究見文獻[5]—文獻[7]。第2種是基于距離測度的相似度度量方法,有代表性的研究見文獻[8]、文獻[9]。第3種思路建立在未知度的再分配基礎上,見文獻[10]、文獻[11]。此外,還有一些具有啟發性的方法。2004年夏少云等[12]、2005年石玉強等[13]提出相似度度量的最小區間法:通過確定Vague值x,y的精確相似度所在的值域,得到它們的最小相似區間。2004年黃國順等[14]提出了基于包含度的Vague集相似度度量方法。由于計算較為復雜,這些方法應用起來不夠簡便。

1 Vague集基本知識

1.1 Vague集定義

設U是一個論域,其中任何一個元素用x表示。U上的一個實數值Vague集A是由真隸屬函數tA和假隸屬函數fA描述[1]:

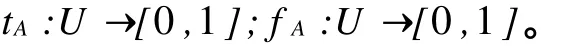
對于x∈U,tA(x)是從支持x∈A的證據所導出的x∈A的肯定隸屬度的下界,fA(x)是從反對x∈A的證據所導出的x∈A的否定隸屬度的下界,并且tA(x)+fA(x)≤1,如圖1所示。x關于A的隸屬度可由[0,1]上的子區間[tA(x),1-fA(x)]表示,或者稱[tA(x),1-fA(x)]是x在Vague集A中的Vague值。

稱πA(x)=1-tA(x)-fA(x)為x關于A的未知度,也稱為猶豫度或躊躇度。πA(x)是x相對于A的未知信息的度量,πA(x)的值越大,說明x相對于A的未知信息越多。當tA=1-fA時,πA(x)=0,即tA(x)+fA(x)=1時, Vague值x退化為普通模糊值。

一般地,Vague集A可記為〈x,tA(x),1-fA(x)〉。當U是連續集時,Vague集A可記為

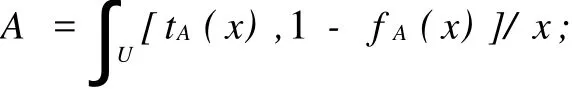
當U是離散集時,Vague集A可記為

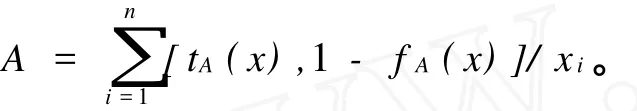
圖1 Vague集示意圖Fig.1 Illustration of Vague sets

論域U中的實數值Vague集全體記為RVVS(U)。

例如,假定X=[1,2,…,10]。Vague集的小數定義為

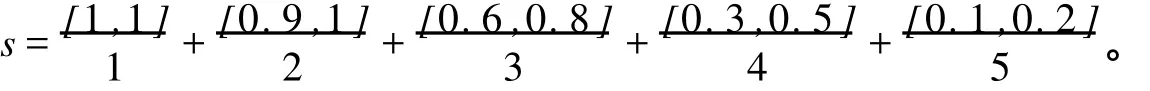
1.2 Vague值相似度基本性質

2個Vague值x,y的相似度sim(x,y)表示x與y的相似程度,x與y的共性越多,sim(x,y)越大;區別越大,sim(x,y)越小。sim(x,y)滿足以下幾個準則:

準則1 (規范性)0≤sim(x,y)≤1;

準則2 (對稱性)sim(x,y)=sim(y,x);

準則3 sim(x,y)=sim(ˉx,ˉy);

準則4[4]sim(x,y)=1?{x,y}={[0,0],[1,1]};

準則5 (單調性)若x≤y≤z,則sim(x,z)≤m in{sim(x,y),sim(y,z)}。

2 基于關聯函數的Vague相似度

2.1 關聯函數的定義

在Vague集上可以定義關聯函數的概念。通過關聯函數值[15],可以定量地描述U中任一元素u屬于肯定域、否定域或未知域3個域中的哪一個,即使同屬于1個域中的2個元素,也可以由關聯函數值的大小區分出不同的層次。

定義真域下界為X0=〈0,tX〉,真域上界為X=〈0,1-fX〉,選擇一點ax∈(1-fX,1],則ax到Vague值 x=〈tX,1-fX〉的關聯函數定義為這里〈〉可為開區間,閉區間、半開半閉區間。

其中,D(ax,X0,X)=ρ(ax,X0)-ρ(ax,X)=(1-fX)-tX,實質上就是未知度。該值越大,說明躊躇度越大,不確定性越高,隱含著真的可信度逐漸增加。

ρ(ax,X)的引入,可以將點與區間的位置關系用定量的形式精確刻畫。當點在區間內時,經典數學中認為點與區間的距離都為0,而在關聯函數中,利用距的概念,就可以根據距的值的不同描述出點在區間內的不同的位置。距的概念對點與區間位置關系的描述,使人們從“類內即為同”發展到“類內也有程度區別”的定量描述。

D(ax,X0,X)描述了2區間之間的關系,形象地刻畫了點ax與區間套X0和X的位置關系。關聯函數k(ax)用于計算點和區間套的關聯程度。描述了真隸屬度下界在真隸屬度上界中的比例。

同理,得到ay到Vague值y=〈tY,1-fY〉的關聯函數定義為

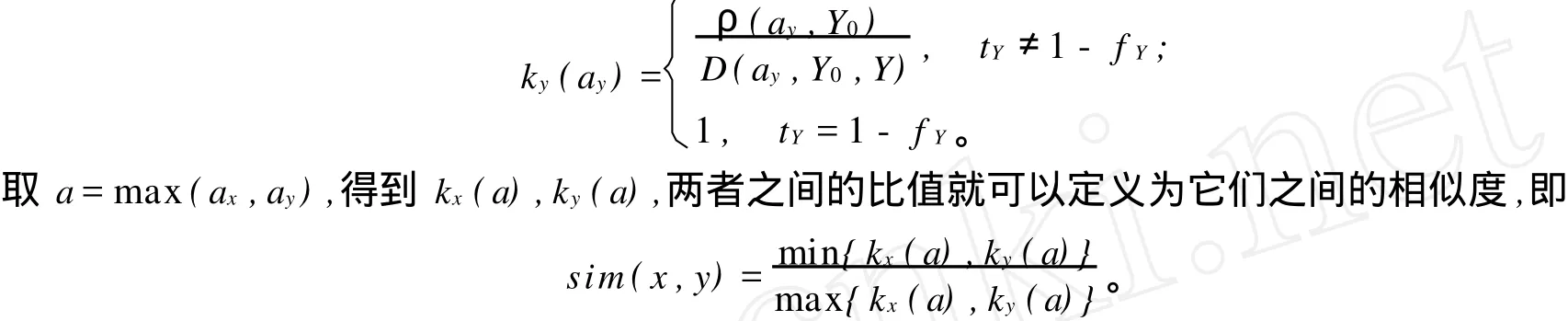
2.2 a值的確定

a值的確定需要從相似性的幾個準則出發,根據以上的定義,相似性的定義滿足準則1,2,4,5,為了滿足準則3,通過a值的確定來實現。

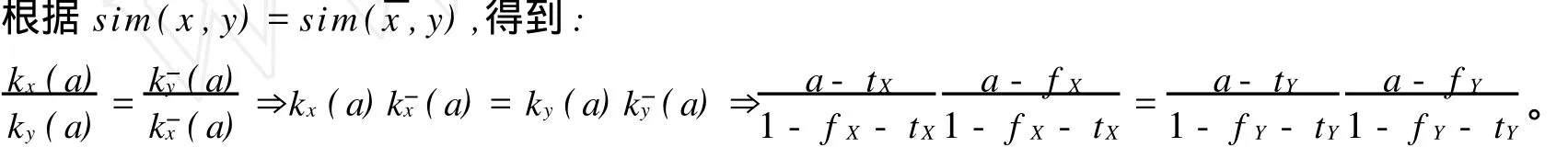
2.3 算例

設Vague值x=[0.4,0.8],y=[0.5,0.8],z=[0.5,0.7],若采用文獻[16]給出的記分函數的方法得到:sim(x,y)=sim(x,z)=0.95,很顯然違反人們的直覺,但是通過以上方法可以得到:sim(x,y)= 0.631 7,sim(x,z)=0.666 7。

因此采用這種方法得到的相似度相對于原來的方法,更加符合人們的感性認識。

3 結 論

文中選擇了統一的定位標準點a作為關聯函數計算的基礎,探討了2個Vague值相對于同一標準的關聯函數,因此,2個Vague關聯函數的計算具備一致性;借助相似度準則,確定了a的取值,保證了相似度函數的可靠性;點與區間距概念的引入,使得2個Vague值相似度的計算有了新的度量標準,從而為相似度的計算搭建了一條新的橋梁。

[1] GAU W L,BUEHRER D J.Vague sets[J].IEEE Trans SMC,1993,23(2):610-614.

[2] A TANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[3] ZADEH L A.Fuzzy sets[J].Inform and Control,1965(8):338-356.

[4] 王偉平.基于Vague集的語言型多準則決策的研究[D].北京:北京理工大學,2008.

[5] CHEN SM.Measuresof similarity between Vague sets[J].Fuzzy Sets and Systems,1995,74(2):217-223.

[6] CHEN SM.Similarity measures between Vague sets and betw een elements[J].IEEE Transactions on System s M an and Cybernetics, 1997,27(1):153-157.

[7] HONGD H,KIM C A.Note on similarity measures between Vague sets and between elements[J].Information Sciences,1999,115:83-96.

[8] SZM IDT E,KACPRZYK J.Distances between intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,2000,114(3):505-518.

[9] L IDeng-feng,CHENG Chun-tian.New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions[J].Pattern Recognition Letters,2002,23(1):221-225.

[10] L IANG Zhi-zhen,SHIPeng-fei.Similarity measureson intuitionistic fuzzy sets[J].Pattern Recoguition Letters,2003,24(15):2 687-2 693.

[11] 周 珍,吳祈宗,劉福祥,等.一種新的基于核函數的Vague集間的相似度量[J].北京理工大學學報(Journal of Beijing Institute Technelogy),2006,26(7):655-658.

[12] 夏少云,查建中,李志輝.Vague集之間相似度量的分析與研究[J].北方交通大學學報(Journal of Beijing Jiaotong University),2004,28 (1):95-99.

[13] 石玉強,王鴻緒.計算Vague集之間的相似度的一種新方法[J].計算機工程與應用(Computer Engineering and App lications),2005,41 (27):178-180.

[14] 黃國順,劉云生.基于包含度的Vague集相似度量[J].小型微型計算機系統(Journal of Chinese Computer Systems),2006,27(5):873-877.

[15] 蔡 文,楊春燕,何 斌.可拓邏輯初步[M].北京:科學出版社,2003.

[16] 李 凡,徐章艷.Vague集之間的相似度量[J].軟件學報(Journal of Software),2001,12(6):922-927.

Similarity measure of Vague value based on extension

CU IChun-sheng
(School of Management and Economics,Beijing Institute of Technology,Beijing 100081,China)

Similarity is very impo rtant in both theory and app licationsof vague sets.Different from the current similarity measures in the field,a new measuremethod was introduced only to p rovide a new idea in the field.In this paper,the concep t of "distance"was first used and a new similarity measure method was given based on the extension depentment function.

Vague sets;similarity measure;extension;depentment function

TP18

A

1008-1542(2010)02-0108-04

2009-12-22;責任編輯:張 軍

河北省教育廳計劃基金資助項目(2007205)

崔春生(1974-),男,青海西寧人,講師,博士研究生,主要從事決策理論與方法方面的研究。