基于質心的樣本加權聚類算法

韋 相,李志勇,朱永繽

(紅河學院計算機科學與技術系,云南蒙自 661100)

0 引 言

聚類分析在模式識別、圖像處理、機器學習等領域有著廣泛的應用,其也是數據挖掘的重要研究領域之一[1].目前,用于數據挖掘的聚類算法主要有4類:以 k-means算法為代表的分割聚類法,以BIRCH為代表的分層聚類法,以DBSCAN算法為代表的密度聚類法和STING為代表的網格聚類法[2-5].其中, BIRCH算法能夠通過一遍掃描進行有效聚類,特別適合大規模的數據集,但該算法采用直徑來控制聚類的邊界,如果子簇非球形,則得不到較好的聚類效果;DBSCAN算法利用類的密度連通特性,可以快速地發現任意形狀的簇,但它效率較低,無法進行動態聚類.本文在 k-means算法基礎上提出了基于質心的樣本加權的分割聚類算法,實驗表明,該算法提高了聚類的精確度.

1 算法的具體描述

1.1 算法的基本思想

本文提出的聚類算法的基本思想是基于物質的質心及物質質心的運動定理.與 k-means聚類算法一樣,本算法聚類的過程就是給每個樣本尋找最近的質心(聚類中心),但與 k-means聚類算法不同,本算法中,質心不僅有位置信息,它還有質量,它的質量就是歸入該聚類中心的樣本的質量總和,當然,每個樣本也有它自己的質量.聚類過程是給每個樣本尋找最近的質心,當某個樣本將歸入某個質心時,該質心的質量就它原有的質量和新歸入樣本質量之和,同時該質心的位置也要根據物質質心的運動定理發生改變.某個樣本原來屬于某個質心,當它要離開該質心歸入新質心時,原質心的質量及位置也發生相應的改變.

1.2 算法的定義

定義1 樣本的特征:數據集的 n個d維樣本(xi),i=1,2,…,n,樣本的聚類特征CF有2個,CF =(mi,si),mi表示xi的質量,它是由xi的非空間屬性決定,si表示xi的位置,由 xi的空間屬性來表示.

定義2 聚類中心的特征:給定具有 n個樣本的數據集(xi),i=1,2,…,n,子簇聚類中心的特征定義為2維CF=(M,S),M表示子簇的質量,它是屬于這個子簇所有樣本的質量總和;S表示子簇聚類中心的位置,它由屬于這個子簇所有樣本的質量和位置決定.

定義3 聚類中心的運動:給定具有 n個樣本的數據集(xi),i=1,2,…,n,一個子簇含有n1個數據點,它的聚類中心特征是 CF=(M,S).

假定有一個新的數據點 y歸入該子簇,那么該子簇的特征向量變化如下:

假定某個數據點原先屬于這個子簇,現在要歸入別的子簇,那這個子簇特征的變化如下:

1.3 算法的實現

本文提出的聚類算法其實現的基本步驟如下:

本算法和 k-means聚類算法的不同之處在于: k-means聚類算法在掃描完所有樣本之后,才調整聚類中心,而本算法是掃描一個樣本,就調整相關的聚類中心.本算法的具體描述如下:

1.4 樣本的權重確定

1.4.1 使用非空間屬性確定.

當對數據集中的樣本沒有任何先驗知識時,可以直接定義每個樣本的權重為1,這時,本算法的聚類效果 k-mean算法相似.本文提出確定樣本權重的方法可根據一些先驗知識,即2個樣本的相異性的計算并不一定要依賴所有的屬性,有些屬性可以用來計算相似度,而有些屬性則可從其他角度對聚類中心產生影響.

對給定具有 n個樣本的d維數據集,(xi),i= 1,2,…,n,(包含d1個空間屬性,可以用來計算相似度,d2個非空間屬性,可以用來計算樣本的權重),可以從相關領域專家那里獲得每個非空間屬性的權重wi,然后再按下式計算樣本的權重,

1.4.2 使用樣本密度確定權重.

在一些數據集中,當樣本只有空間屬性,而沒有用于計算權重的非空間屬性時,則可以用別的方法計算樣本的權重.對那些處于稠密區域中的樣本(即周圍被更多樣本包圍),其必將對聚類中心產生更大的影響.對此,可采用點密碼的思想:樣本 p的Eps鄰域密度,用N(p)表示,它表示在樣本 p的Eps鄰域的樣本數目,用它作為樣本 p的權重.

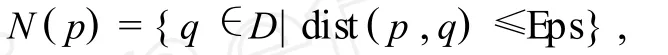
2 實 驗

在實驗中,我們將本文的算法和 k-means算法的聚類結果進行了比較.測試數據為 IRIS和Soybean-small數據(這2組測試數據都來自網站:http:// archive.ics.uci.edu,它們是用來進行聚類分析的標準數據集).IRIS有150個樣本,分為3個子類,每類有50個樣本,其中2個子類具有交叉的樣本,很難對這些交叉樣本進行準確的分類.

2.1 對IRIS數據的聚類結果

采用本文提出算法對IRIS數據的聚類結果見表1.采用 k-means算法對IRIS數據的聚類結果見表2.

表1 本文算法對IRIS的聚類結果

表2 k-means算法對IRIS的聚類結果

從表1、2可見,k-means算法把第2類的3個樣本,錯誤的歸入第3類,而把第3類14個樣本錯誤的歸入第2類,共有17個錯分的樣本,準確度是88.7%;而本文提出的算法總共有14個錯分的樣本,算法的準確度為90.7%.顯然,本文的算法有效且具有更高的精確度.

2.2 對Soybean-small數據的聚類結果

Soybean-small數據具有47個樣本,每個樣本有35個屬性,共分為4個子類,其中一個類包含17個樣本,另外3個類各有10個樣本.因為這些屬性中有14個屬性值是完全相同的,所以我們只使用另外21個屬性進行聚類分析.本文算法的聚類結果見表3,用 k-means算法的聚類結果見表4.

表3 本文算法對Soybean-small數據的聚類結果

表4 k-means算法對Soybean-small數據的聚類結果

從表3、4可見,使用k-means算法,它錯分了15個樣本,準確度是66%;而本文的算法僅錯分了12個樣本,準確度是74.5%.同樣,本文算法的聚類結果精度更優.

3 結 論

依據不同樣本對聚類中心產生不同影響,我們提出了基于樣本加權的聚類算法,并針對具體數據集,把樣本屬性分為空間屬性和非空間屬性,這樣可以提高聚類算法的應用領域.實驗表明,該算法比k-means聚類算法具有更高的精確度.下一步的研究方向為:一是引入模糊數學,實現模糊聚類,提高邊界處理能力;二是把該算法應用于圖像分割等領域.

[1]Han J,Kamber M,Tung A K H.Spatial Clustering Methods in Data Mining:A Survey[M].New Y ork:John Wiley,2001.

[2]Jain A K,Murty M N,Flynn1 P J.Data clustering:A review [J].ACM Computing Surveys,1999,31(3):1145-1149.

[3]Zhang T,Ramakrishnan R,Linvy M.Birch:an Efficient Data Clustering Method for very Large Databases[C]//Proceeding of ACM SIGMOD International Conference.New Y ork:ACM Press, 1996.

[4]Ester M,Kriegel H,Sander J,et al.A Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise [C]//Proceeding of2nd International Conference on Knowledge Discovery and Data Mining.Portland,Oregon:ACM Press,1996.

[5]Wang W,YangJ,Myntz R.Sting:a Statistical Information Grid Approach to Spatial Data Mining[C]//Proceedings of the23International Conference on Very Large Databases Athens.New Y ork:ACM Press,1997.