基于ABAQUS的邊坡失穩綜合判據法

蔡路軍，馬建軍，周大華，劉 松，潘 欣

（1.武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北武漢，430065；2.湖北省十堰至白河高速公路建設指揮部，湖北十堰，442000）

1 常用邊坡失穩判據

采用強度折減有限元法分析邊坡穩定性的一個關鍵問題是如何根據有限元計算結果來判別邊坡是否達到極限破壞狀態。目前常用的邊坡失穩判據主要有：（1）有限元計算不收斂；（2）坡體或坡面位移突變；（3）潛在滑移面塑性區貫通。

采用第1種判據的理由是：有限元計算迭代過程就是尋找外力和內力達到平衡狀態的過程，整個迭代過程直到一個合適的收斂標準得到滿足才停止，如果邊坡失穩破壞，滑面上將產生沒有限制的塑性變形，有限元程序無法從有限元方程組中找到一個既能滿足靜力平衡又能滿足應力－應變關系和強度準則的解，此時不管是從力的收斂標準，還是從位移的收斂標準來判斷，有限元計算都不收斂。這樣處理自然可以避開臨近極限狀態的計算，但采用有限元計算不收斂作為破壞標準包含一定的非確定性人為因素，并且在有些情況下計算結果可能會有較大誤差，因為不收斂可由多種原因引起，比如荷載步長過大或體系內不同部分的剛度相差懸殊而使其數值性態較差。另外，有限元數值計算收斂時也不一定表明邊坡處于安全狀態[1－6]，因此將有限元計算的收斂性作為邊坡的失穩判據不具備廣泛的適用性。

采用第2種判據的理由是：由理想彈塑性材料構成的邊坡進入極限狀態時，必然是其一部分土體相對于另一部分發生無限制的滑移。盡管各種因素對位移和塑性應變等計算結果有較大影響，但這些因素不能改變邊坡瀕臨破壞時位移突變的本質趨勢，因此建議采用特征點處的位移突變作為邊坡處于極限狀態的判據，這樣可以減小非確定性因素對安全系數的影響，但是該方法中特征點的選取對安全系數計算結果的影響較大[7]。

第3種是以邊坡的等效塑性應變區從坡腳到坡頂貫通作為邊坡發生整體失穩破壞的判據[8－10]。這種方法物理意義明確，但也有其不精確之處，因為在進入極限狀態前，土工結構的塑性區也可能是貫通的，并且區域還可能較大。例如在計算一水平土層的自重應力時，如果土層的泊松比偏小，則開始計算時由于土體內剪應力水平較高，整個土體均處于塑性區。但通過彈塑性計算，土體內水平應力增大，而體系保持穩定并不破壞。所以，由計算顯示的塑性區貫通來認定極限狀態也是一種近似處理。另外，文獻[4]認為，邊坡破壞的特征是廣義剪應變從坡腳到坡頂上下貫通，其物理意義較明確，但廣義剪應變不僅含有塑性分量，而且也包括彈性分量，雖然廣義剪應變的大小能夠在一定程度上反映土體的剪切破壞狀態，但是并不能準確地描述土體塑性區的發生與發展過程。因此，根據廣義剪應變來判斷塑性區及剪切破壞區的發展，并以此作為判斷失穩的指標還是不夠合理和準確。

上述3種判據都有其局限性，因此在采用強度折減有限元法計算邊坡穩定安全系數時，筆者認為宜聯合采用特征點處的位移突變和塑性區是否貫通等作為邊坡失穩的判據，并且在用特征點位移突變作為判據時，應盡量在坡頂和坡趾處的特征部位設立多個觀察點，以考察其位移與塑性區隨強度折減系數的變化規律。

2 綜合判據法

強度折減有限元法和極限平衡法實質上都是基于塑性力學理論的極限分析方法，因此這兩種方法的分析過程和計算結果應該具有一致性，故一般采用小應變分析，此時數值不收斂判據是可行的。但邊坡在失穩過程中，可能產生大應變問題，這時就不能用數值不收斂作為判據了，否則會導致結果偏大。為了使數值計算在邊坡破壞后能收斂，應采用大應變分析，并建立位移突變判據。

塑性區貫通是邊坡破壞的必要條件，但不是充分條件，考慮到塑性區貫通的客觀指標很難確定，目前只能通過人的主觀判斷，從而不可避免地增加不確定性人為因素，因此在實際應用過程中，塑性應變區貫通的判據可作為前兩種判據的補充。

綜上所述，綜合判據法步驟如下：

（1）進行小變形有限元計算，以計算不收斂為邊坡失穩判據。對給定的抗剪強度參數折減，進行小變形有限元計算，直至計算不收斂，得出安全系數F1。

（2）進行大變形有限元計算，以位移突變為判據。以邊坡上某幾點為監測點分析其位移與折減系數的關系，擬合曲線，得出安全系數F2。

（3）在上述兩種方法中，觀察塑性應變區貫通狀況，如出現異常再進行討論。通過綜合分析比較，得出合理的安全系數F。

在進行有限元計算時，應用的軟件是ABAQUS。ABAQUS是一套功能強大的工程模擬有限元軟件，其解決問題的范圍從相對簡單的線性分析到許多復雜的非線性問題。ABAQUS是目前處理巖土工程問題時應用較廣的計算軟件，其涵蓋豐富的材料模型庫，可以較為準確地模擬巖土這種特殊材料，在解決巖土力學中復雜的非線性問題方面優勢顯著。

3 標準算例

本文選擇澳大利亞計算機應用協會（ACADS）的一道考核題作為標準算例，利用強度折減有限元法來比較采用各種失穩判據獲得的邊坡穩定性系數，并與采用不同條分法計算得到的結果以及參考答案進行比較，綜合分析各種判據的適用條件。該算例為一均質邊坡，坡高H＝10 m，坡角β＝26.6°，土體密度ρ＝2 t／m3。為了與傳統的極限平衡法計算結果進行比較，土體計算采用理想彈塑性本構模型、莫爾－庫侖屈服準則和相關聯流動法則，黏聚力c＝32 k Pa，內摩擦角φ＝10°，膨脹角ψ＝φ，彈性模量E＝10 MPa，泊松比μ＝0.25。

均質邊坡的有限元分析模型和網格劃分如圖1和圖2所示。網格劃分為1 012個單元、1 084個節點。邊坡分析模型的左右邊界均采用水平約束，底面采用水平豎向約束。

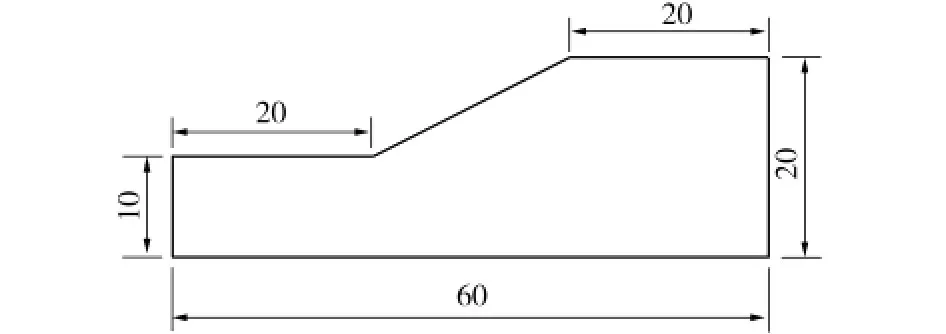
圖1 邊坡分析模型Fig.1 Model of the slope

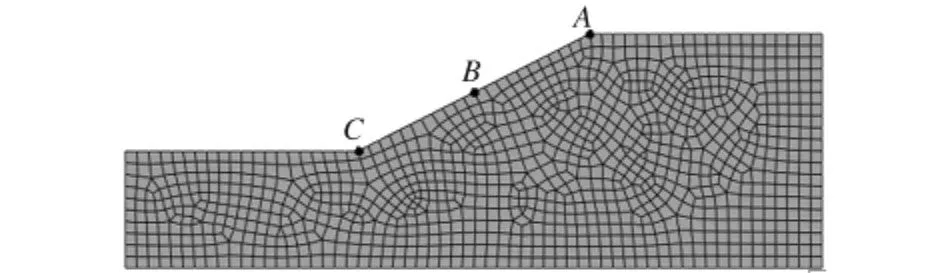
圖2 邊坡有限元網格劃分Fig.2 FEM mesh of the slope

3.1 小變形計算

應用小變形計算方法，要求精度達到0.001，通過計算，最后確定安全系數為1.698。應用小變形計算方法時邊坡塑性應變如圖3所示。此時，位于頂端的39＃節點A、中部的43＃節點B、底部的47＃節點C的位移如表1所示，其中U1、U2和U分別為節點的水平位移、垂直位移和總位移。

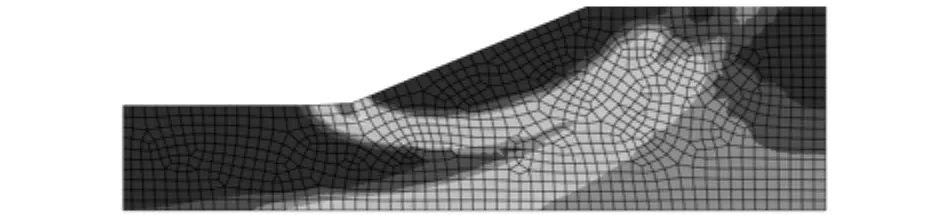
圖3 邊坡等效塑性應變圖Fig.3 Equivalent plastic strain distribution of the slope

3.2 大變形計算

應用大變形計算方法，得出A、B、C點的位移如表2所示。

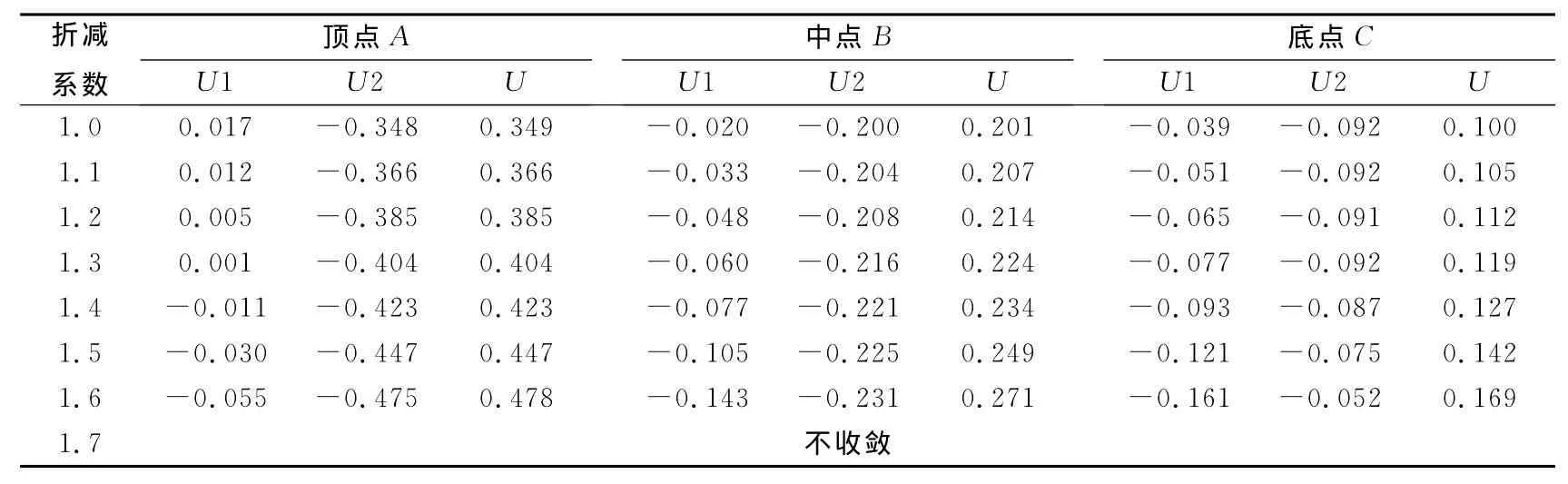
表1 小變形計算位移量Table 1 Displacement of small deformation calculation

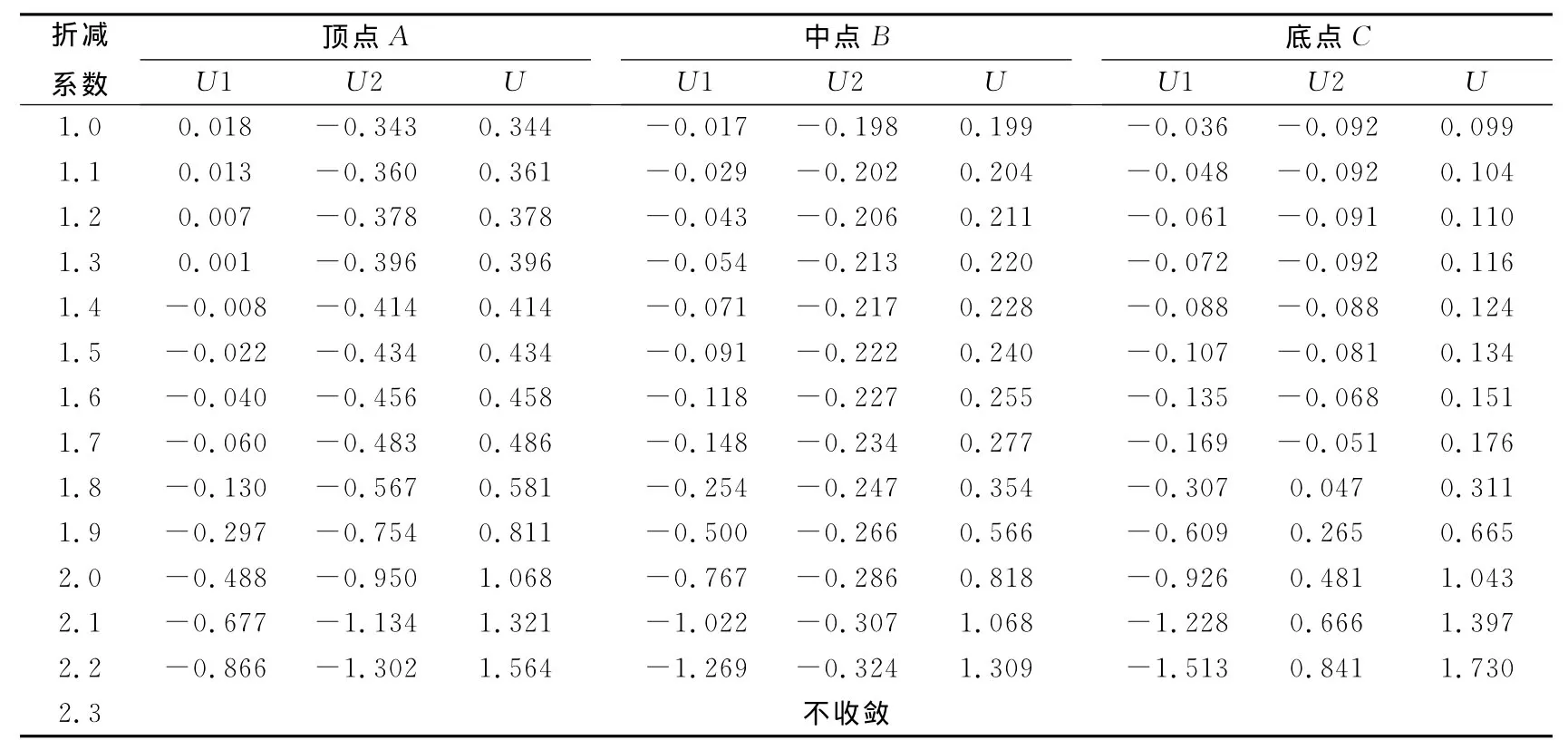
表2 大變形計算位移量Table 2 Displacement of large deformation calculation

A、B、C點的水平位移與折減系數的關系如圖4所示。從圖4中可以看出，當折減系數達到1.70后，各點水平位移明顯出現較大的增量，因此可近似認為安全系數為1.70～1.80。從3條曲線的切線擬合情況來看，可進一步將安全系數定為1.70。

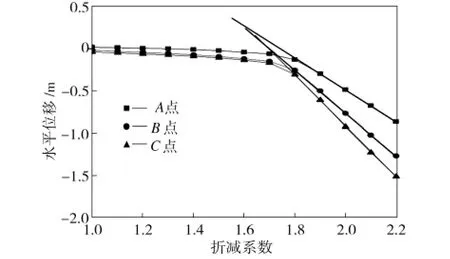
圖4 節點水平位移與折減系數的關系Fig.4 Relationship between horizontal displacement and reduction factor

在不同的折減系數K下，A、B、C點的水平位移發展過程如圖5所示。從邊坡的塑性應變（見圖3）和水平位移的發展過程可以看出，邊坡失穩過程大致可分為3個階段：（1）穩定發展階段。重力載荷開始施加時，潛在滑移面周圍的土體單元產生塑性應變，但坡體位移變化不大。（2）滑移帶初步形成，位移增大階段。隨著載荷增加，坡體位移增大，塑性應變也增大，土體塑性區沿著滑動面向上爬升，直至坡體內的滑移帶初步形成。（3）位移突變，坡體失穩階段。如果載荷繼續增大，則坡體位移急劇增大，邊坡沿滑移帶發生整體失穩，塑性應變貫通。

3.3 結果分析

以有限元計算不收斂為邊坡失穩判據，對邊坡穩定進行小變形有限元計算，得出安全系數為1.698，強度折減有限元法搜索到的潛在滑動面與傳統的極限平衡法得到的結果一致；再以位移突變為邊坡失穩判據，進行大變形有限元計算，得出安全系數為1.70。綜合分析小變形和大變形計算條件下的邊坡安全系數，再結合塑性區貫通情況，可確定其安全系數為1.70。

對于此例，采用極限平衡法中的簡化Bishop法計算得出的安全系數為1.687，ACADS對該算例給出的邊坡安全系數參考值為1.65～1.70。本文得出的結果與ACADS給出的參考值較為接近，與簡化Bishop法的結果相差僅0.76%，這證明了本文方法的可行性與準確性。

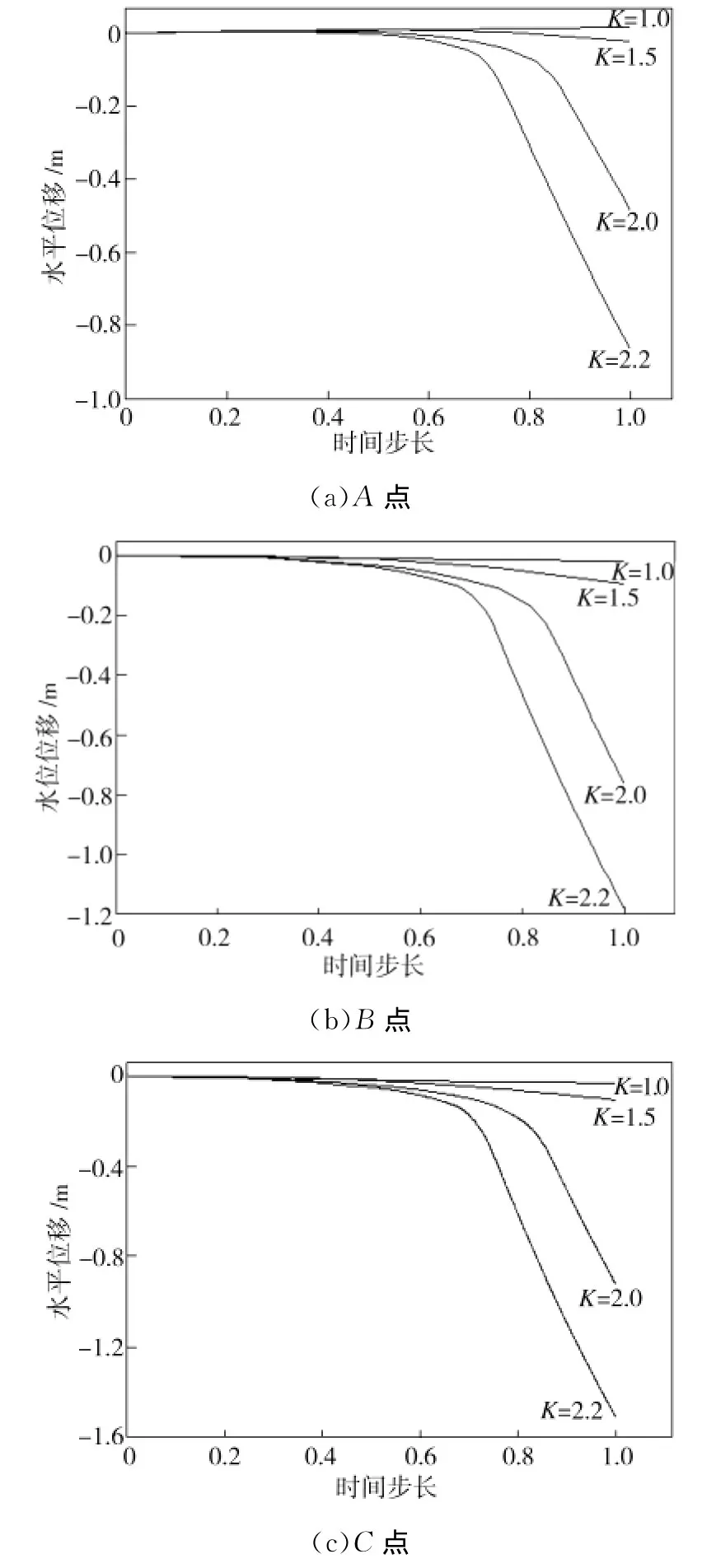
圖5 節點水平位移與時間步長的關系Fig.5 Relationship between horizontal displacement and time step

4 工程實例

某一基坑開挖深度為3.0 m，采用1∶1放坡開挖。參照文獻[3]對計算區的研究結論，計算范圍取為總寬度18 m，深度10 m，具體尺寸如圖6所示。土層分為3層：第1層為雜填土，ρ＝1.8 t／m3，E＝5 MPa，c＝15 k Pa，μ＝0.3，φ＝23°，厚度為1.0 m；第2層為淤泥質粉質黏土，ρ＝1.9 t／m3，E＝3 MPa，c＝5 kPa，μ＝0.45，φ＝16°，厚度為3.0 m；第3層為粉土與粉砂互層，ρ＝1.78 t／m3，E＝10 MPa，c＝10 k Pa，μ＝0.45，φ＝16°，厚度為6.0 m。約束條件：右側和左側坡底下為水平向約束，底面為水平和豎向雙向約束的鉸接約束。

采用本文提出的方法，以計算不收斂為邊坡失穩判據，對邊坡穩定進行小變形有限元計算，得出安全系數為1.278，分別采用強度折減有限元法和傳統極限平衡法搜索到的潛在滑動面具有一致的結果；再以位移突變判據，進行大變形有限元計算，得出安全系數為1.30。綜合分析小變形和大變形計算條件下的邊坡安全系數，并結合塑性區貫通情況，可確定其安全系數為1.30。采用極限平衡法中的簡化Bishop法對此例計算得出的安全系數為1.276，二者很接近，再次證明了綜合判據法的合理可行。

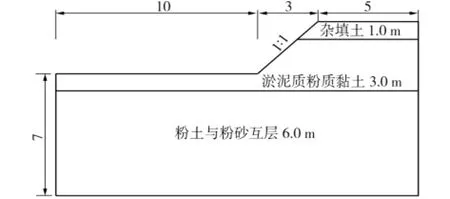
圖6 開挖邊坡示意圖Fig.6 Schematic diagram of the foundation slope

5 結語

在采用強度折減有限元法進行邊坡穩定性分析的過程中，采用綜合判據法對邊坡是否達到極限狀態進行判定，不會出現以偏概全的極端情況，可更準確地計算邊坡安全系數，所得結果與采用傳統極限平衡法得到的計算結果吻合良好。但綜合判據法的缺點是計算較為復雜，其中在大變形計算時以位移突變作為判據存在人為因素，難以精準控制。

[1] Griffiths D V，Lane P A.Slope stability analysis by finite elements[J].Geotechnique，1999，49（3）：387－403.

[2] Dawson E M，Roth W H，Drescher A.Slope stability analysis by strength reduction[J].Geotechnique，1999，49（6）：835－840.

[3] 張魯渝，鄭穎人，趙尚毅，等.有限元強度折減系數法計算土坡穩定安全系數的精度研究[J].水利學報，2003，34（1）：21－27.

[4] 趙尚毅，鄭穎人，張玉芳.有限元強度折減法中邊坡失穩的判據探討[J].巖土力學，2005，26（2）：332－336.

[5] 劉金龍，欒茂田，趙少飛，等.關于強度折減有限元方法中邊坡失穩判據的討論[J].巖土力學，2005，26（8）：1 345－1 348.

[6] 佀赟，皇甫軍.有限元強度折減理論求安全系數及存在的問題[J].西部探礦工程，2007，19（2）：203－206.

[7] 宋二祥，高翔，邱玥.基坑土釘支護安全系數的強度參數折減有限元方法[J].巖土工程學報，2005，27（3）：258－263.

[8] 連鎮營，韓國城，孔憲京.強度折減有限元法研究開挖邊破的穩定性[J].巖土工程學報，2001，23（4）：406－411.

[9] 欒茂田，武亞軍，年廷凱.強度折減有限元法中邊坡失穩的塑性區判據及其應用[J].防災減災工程學報，2003，23（3）：1－8.

[10] 鄭宏，李春光，李焯芬，等.求解安全系數的有限元法[J].巖土工程學報，2002，24（5）：625－628.