球面4R機構運動特性研究及其應用探索

周香琴

浙江理工大學，杭州，310018

球面4R機構運動特性研究及其應用探索

周香琴

浙江理工大學，杭州，310018

為了運用球面4R機構滿足周期性往復運動的需求，以GTM劍桿織機中球面4R引緯機構為研究對象，建立了機構的結構參數和輸出運動參數之間的函數關系，利用數學方法得出了機構運動函數的特性，分析了各結構參數對運動曲線形態的影響。通過組合相關的結構參數，獲得了不同形態的運動曲線，實現了機構的變異，擴展應用到引緯機構的擴幅設計和開口機構的創新設計中。研究結果表明，通過合理組合球面4R機構中的兩個結構參數可以實現多種應用。

球面4R機構；運動特性；曲線形態；劍桿織機；引緯

0 引言

引緯機構是劍桿織機的核心機構，它決定了織機的車速。在高檔的劍桿織機中，球面4R機構（用于引緯驅動）因其結構緊湊、運動副簡單、加工安裝方便、成本低并且適應高速工況而深受歡迎。RSSR機構、4R機構目前的研究大多為理論研究［1－5］。從工程實際要求出發，有針對性地研究運動特性，為工程應用提供理論依據的應用基礎研究比較少見。筆者通過數學論證和數值計算相結合的方法，分析該機構的運動特性，建立相關機構參數與運動性能之間的映射關系，通過組合設計有關參數，達到機構創新的目的，擴大機構的應用領域，為靈活運用4R機構提供方法和思路。

1 GTM劍桿織機引緯機構介紹

GTM劍桿織機是比利時PICANOL公司于20世紀90年代生產的劍桿織機。圖1所示為該機的引緯驅動機構。與主軸固連的旋轉臂1通過滾針軸承與叉形連桿2連接，叉形連桿2與十字節3通過推力軸承連接，十字節通過軸承固定在箱體上。旋轉臂1、叉形連桿2與十字節3上的所有運動副軸線交于一點C，形成一個球面4R機構，從而起到調節引緯動程的作用。十字節3和扇形齒輪5通過中心分別位于E點和F點的軸承與H形連桿4連接，扇形齒輪5通過中心位于G點的軸承與箱體連接，形成了一個平面四連桿機構，鉸接點F在扇形齒輪的長槽上滑動，用以改變扇形齒輪的擺幅大小，起到調節引緯門幅的作用。扇形齒輪5與傳劍軸6上的齒輪嚙合 ，實現引緯動程的放大。傳劍軸6通過固定在其上的劍輪，帶動劍頭和劍帶運動，實現劍桿織機的引緯功能。

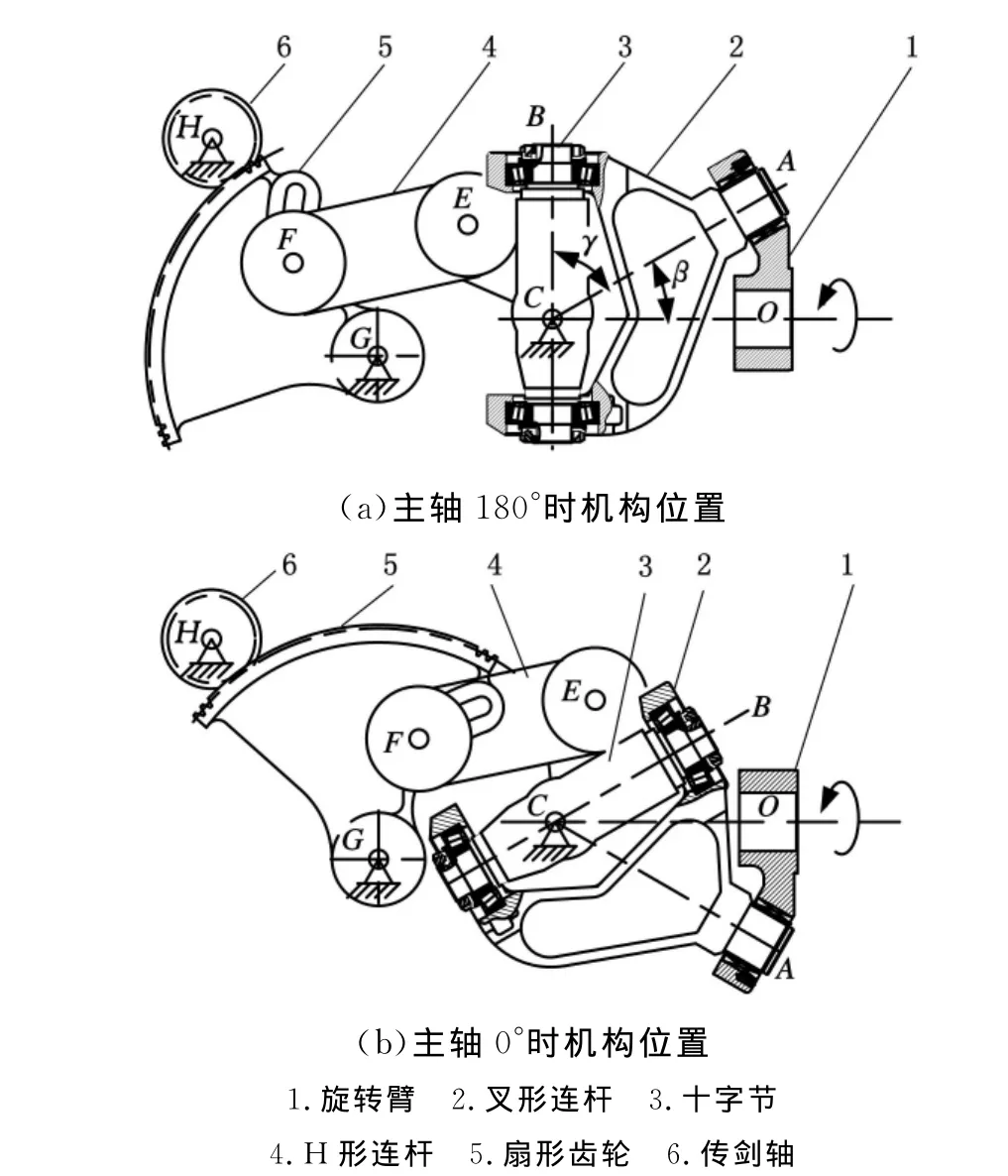
圖1 GTM劍桿織機引緯驅動機構

圖1a、圖1b所示分別為GTM劍桿織機主軸處于180°（兩劍頭交接緯紗的位置）和0°時的位置，旋轉臂1在正常織造時的轉動方向為圖1所示方向。由于有了一套平面四連桿機構，其中，扇形齒輪上用于調節F、G間距的長槽可以根據需要設計。在GTM劍桿織機中，當織機主軸處于180°時，E點處于引緯動程調節長槽的圓心上（圖1a的位置），此時F點沿圓弧槽改變位置，扇形齒輪的位置不會改變，即劍頭的位置不會改變，所以采用該方法調節劍頭動程可以實現劍頭交接緯紗時刻位置不變，操作簡便。通過以上的分析，我們可以得到GTM劍桿織機引緯驅動機構簡圖（圖2）。

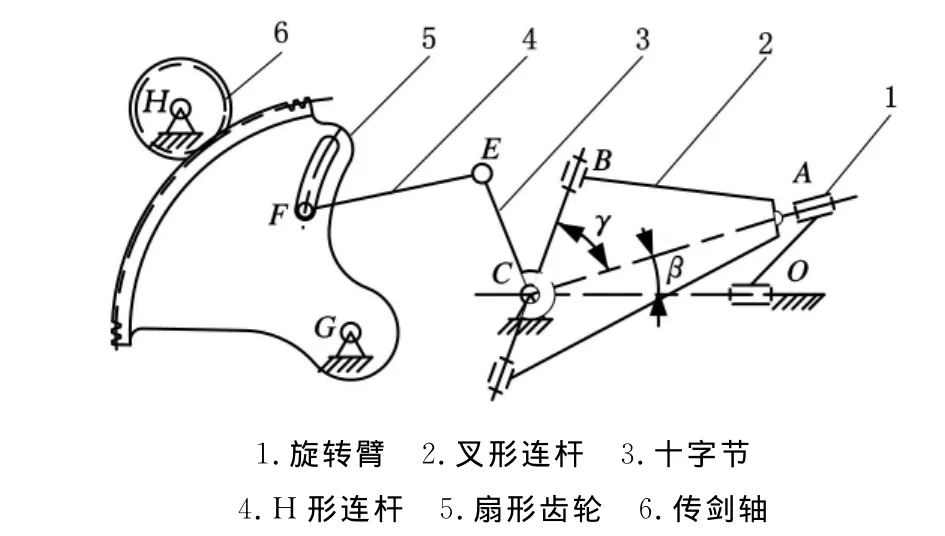
圖2 GTM劍桿織機引緯驅動機構簡圖

2 球面4R機構運動函數的推導

由前面的分析可以看出，引緯運動的規律變化主要是由OABC球面的4R機構控制的，該機構的輸入構件為旋轉臂1，輸出構件為十字節3，它們的運動方向正交。下面重點分析該機構的運動函數。

在旋轉臂與叉形連桿的相對運動軸線AC上取一點A，在旋轉臂的轉動中心軸線OC上取一點O，使OA⊥OC，假設O、A兩點的間距為L1，旋轉臂上兩運動副軸線OC與AC的夾角為β。在叉形連桿與十字節的相對運動軸線BC上取一點B，假設A、B兩點的間距為L2，叉形連桿上兩個運動副軸線AC與BC的夾角為γ。假設十字節上兩點B、C的間距為L3，機架上兩點O、C的間距為L4，A、C兩點的間距為L5。以O點為坐標原點，OC所在的直線為X軸，CB的運動平面為OXY平面，建立如圖3所示的直角坐標系。

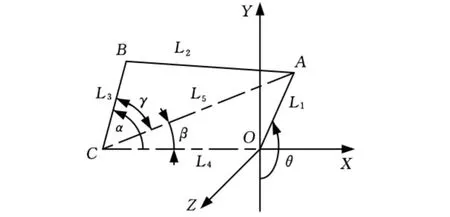
圖3 球面4R機構結構參數示意圖

θ為OA在OYZ平面內的轉角。α為CB在OXY平面內的轉角，θ與α的起始位置和正向如圖3所示。

根據前面的分析可知：OA 在OYZ平面內繞X軸做圓周運動，BC在OXY平面內繞C點做擺動，AB繞C點做空間運動。

式（7）為球面4R引緯機構的運動函數方程，因為γ為叉形連桿的結構參數，β為旋轉臂的結構參數，根據式（7）可以得到α＝f（θ）的函數對應關系。在實際機構中，重點要研究的是f（θ）－f（0°）與結構參數γ和β之間的關系。現假設α1＝η（θ）＝f（θ）－f（0°）。

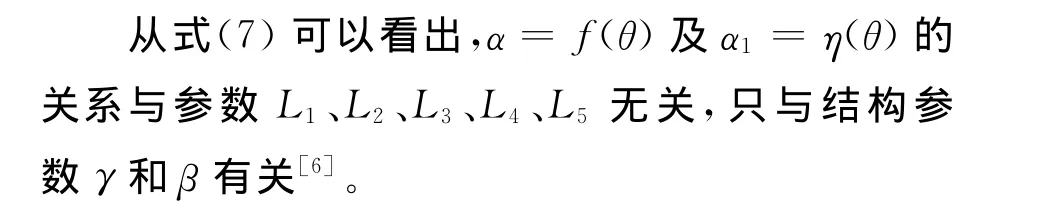
3 函數特性研究

3.1 函數的對稱性和機構存在條件

3.2 函數的單調性

對式（7）求一階導數并整理后得到

3.3 極值

3.4 γ＝90°時的函數性質

3.5 γ＝c與γ＝180°－C時函數之間的關系

3.6 結構參數β、γ對函數形態的影響

在實際的GTM引緯驅動機構中，β＝30°，γ＝60°。劍頭劍帶的動程與十字節的初始角無關。前面的討論中，θ以逆時針方向為正，但實際機構中，正常運轉時θ以順時針方向運轉。由于η（θ）關于θ＝0°對稱，所以旋轉臂1順轉和逆轉的規律相同，前面的討論能代表實際機構的運行情況。另假設ζ（θ）＝f（θ）－f（180°）。

固定γ＝60°，分別取β＝10°，20°，30°，35°，40°，為了便于討論運動曲線的形態，把不同β值對應的曲線通過一個系數M（β）修正，使函數的極值相同。假設ξ（θ）＝ M（β）η（θ），求得相應的ξ（θ）（θ）、（θ），得到圖6所示的曲線規律。其中M（β）是一個只與結構參數β有關的系數。

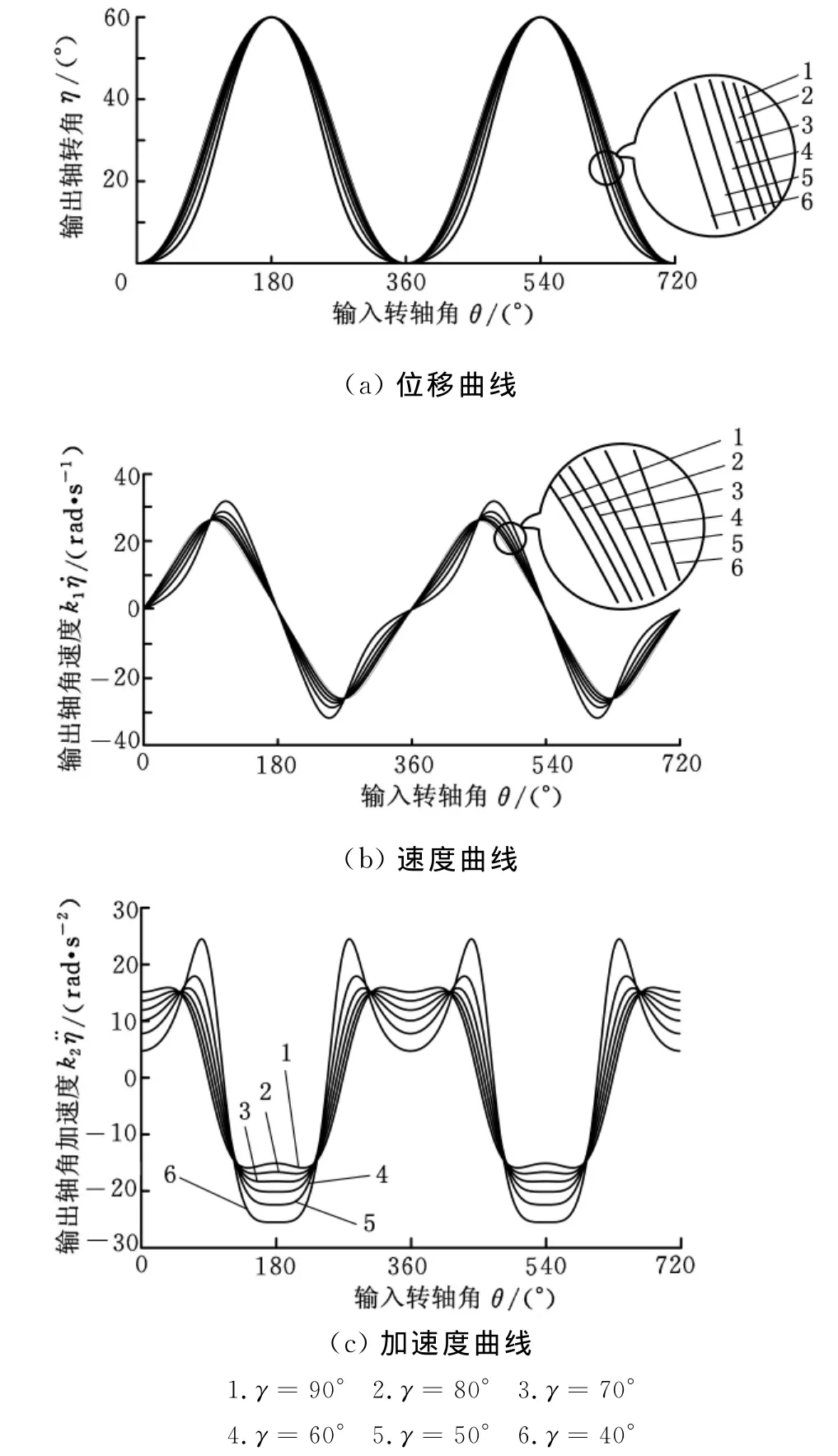
圖4 γ對運動函數形態的影響（30°＜γ≤90°）

3.7 討論

通過上文的分析可知，隨著γ的增大，加速度和速度的最大值減小，位移曲線在0°附近比較平緩，在180°附近相對陡一些。γ大于90°后，隨著γ的增大，加速度和速度的最大值增大，位移曲線在180°附近比較平緩，在0°附近相對陡一些。ζ（θ＋關于θ軸對稱，與3.5節的結論一致。

從圖4、圖5可以看出，γ＝90°時η加速度曲線比較平緩，速度曲線關于θ＝90°，θ＝270°對稱，位移曲線在0°和180°附近平緩程度相同，與3.4的結論一致。

通過上文的分析，并從圖6可知，隨著β值的加大，最大加速度、最大速度值在加大，位移曲線在0°附近逐漸趨于平緩，在180°附近變化不明顯。

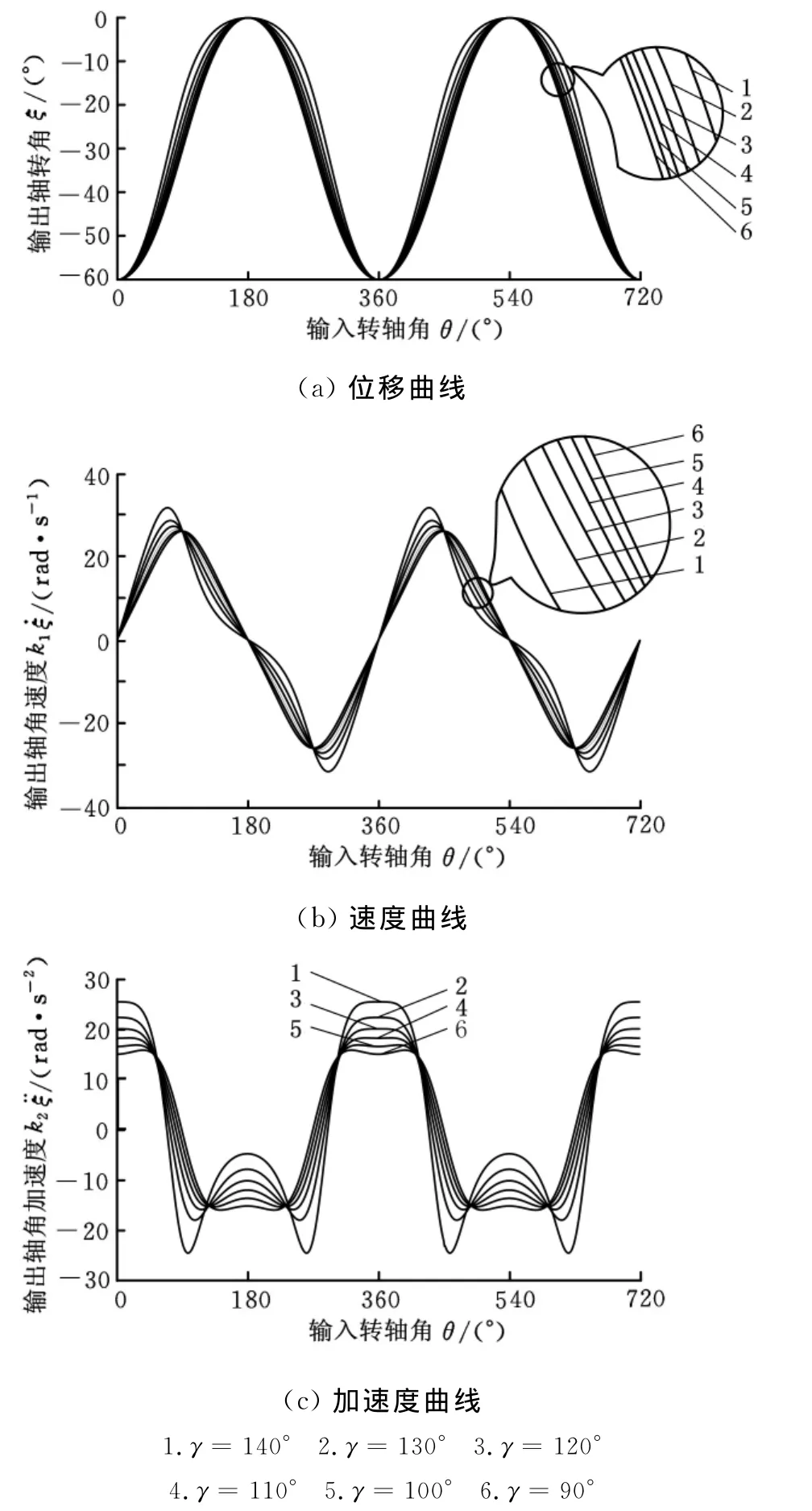
圖5 γ對運動函數形態的影響（90°≤γ＜150°）

4 應用探索

4.1 增加總動程減少空動程的應用

在實際的引緯機構設計中，劍頭的運動規律需要與打緯和開口的運動規律相配合，劍頭進入梭口的時間是有規定的，劍頭在梭口外的動程一般稱為空動程。在引緯機構的設計中，特別是在寬幅織機的設計中，控制空動程是一項重要的任務。空動程大，機器的占地面積大、剛性差；空動程小，引緯的最大速度、最大加速度大。在GTM劍桿織機中，引緯機構能適應的最大織機門幅是280cm。采用增大齒輪傳動比的辦法，可以達到增大引緯門幅的效果，但是空動程也按總動程的比例一起增大，若采用這種方法擴大門幅，整個引緯機構的結構更改大、成本高。根據前面的討論分析可知，可以采用增大β、減小γ來達到增大總動程、減小空動程的效果，并且保證β＋γ的值不變，保證機構的外形尺寸不變。為配合齒輪速比的適當變化，在保證強度的前提下，更換少量的零件，來滿足引緯機構擴幅的要求，通過這種方法成功地將該引緯機構的適應門幅增加到360cm。

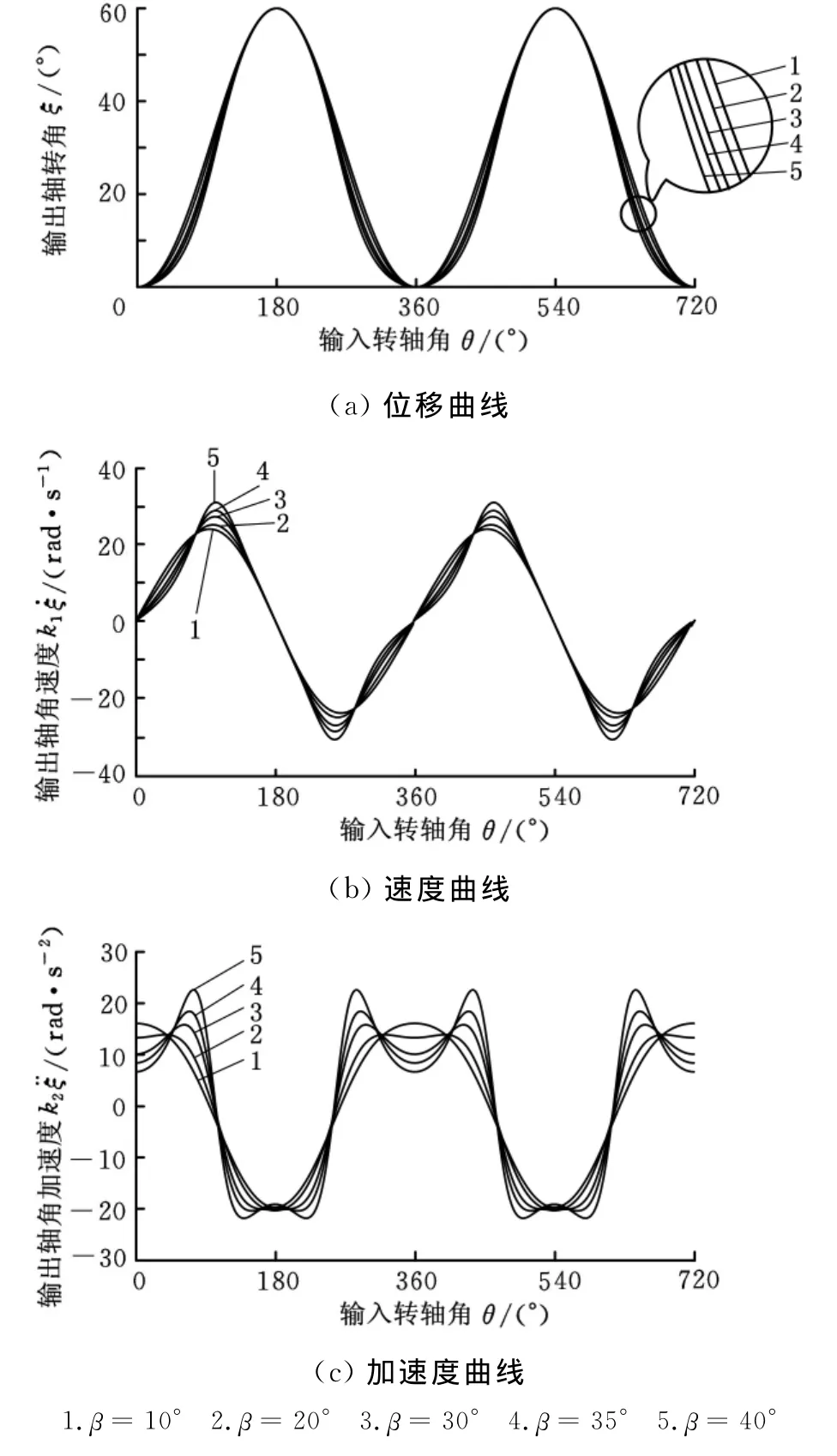
圖6 β對運動函數形態的影響（0°＜β≤90°）

4.2 運動曲線反向的應用

在劍桿織機中，引緯機構的外形尺寸和結構布局往往影響整臺織機的結構。針對不同的門幅，為了較好地設計系列型劍桿織機，引緯驅動機構的結構點的位置和外形尺寸最好變化不大或者不變，不影響周邊的部件和墻板的結構。4.1節的應用完全符合這個要求，但要想再擴大門幅到540cm或更大，一味地增大β、減小γ已經不能滿足要求了，需要增加一級齒輪傳動，但這帶來了劍頭劍帶運動方向改變的問題。

通過前文的討論分析，我們可以看出，在其他參數相同的情況下，可以通過改變γ和輸入參數θ的起始位置改變位移曲線的形態，滿足位移、速度、加速度規律曲線的反向要求。利用這種方法成功地完成了門幅為540cm的劍桿織機引緯驅動機構的設計，通過分析，可以繼續擴幅，應用到門幅達1000cm的劍桿織機上。劍桿織機機構如圖7所示，圖7中的主軸處于180°時的位置。與圖2中的機構相比，增加了過渡齒輪7和過渡齒輪軸8（分別與傳劍軸6上的齒輪和扇形齒輪5嚙合），十字節3和叉形連桿2的連接方式改變了，90°＜γ＜180°－β。但外形尺寸和主要結構點位置基本沒變，實現了引緯驅動機構的擴幅設計。

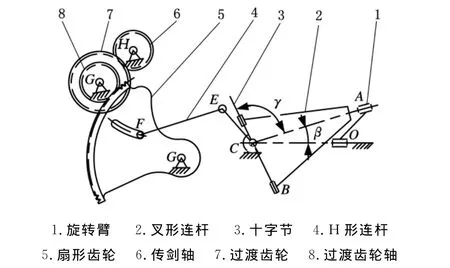
圖7 特寬幅引緯驅動機構原理圖

4.3 在開口機構上的應用

根據前文的分析可知，γ＝90°時的球面4R機構能符合復動式開口驅動的基本要求，織機中綜框的運動平面與主軸的運動平面垂直，且主軸轉兩圈，綜框來回運動一次。在一般的織機中，主軸到開口機構的運動傳輸是通過一級同步帶實現的，通過一級錐齒輪實現運動方向和運動速度的改變，再通過凸輪或偏心輪機構實現綜框的開口運動規律要求。運用前面討論的空間連桿機構可以實現兩個功能，即運動方向的轉變和開口運動規律的產生。開口機構要求的速比變化可以在同步帶傳輸時實現，這樣就可以減少一級錐齒輪的傳動，簡化了結構，降低了成本。如圖8所示，主動同步帶輪1與主軸固定，通過同步帶2帶動被動同步帶輪3運動，實現運動的遠距離傳遞和速度的變化，旋轉臂4與被動同步帶輪固定，通過由旋轉臂4、空間連桿5、開口刀片6和機架組成的球面4R機構實現運動的轉向和開口運動規律的生成，開口刀片通過多臂連桿（連桿機構）帶動綜框，實現織機的開口。該機構的缺點是只能適用于平紋開口，比較適合窄幅，優點是該裝置結構簡單、運動副少、成本低，而且比較適于高速運動。

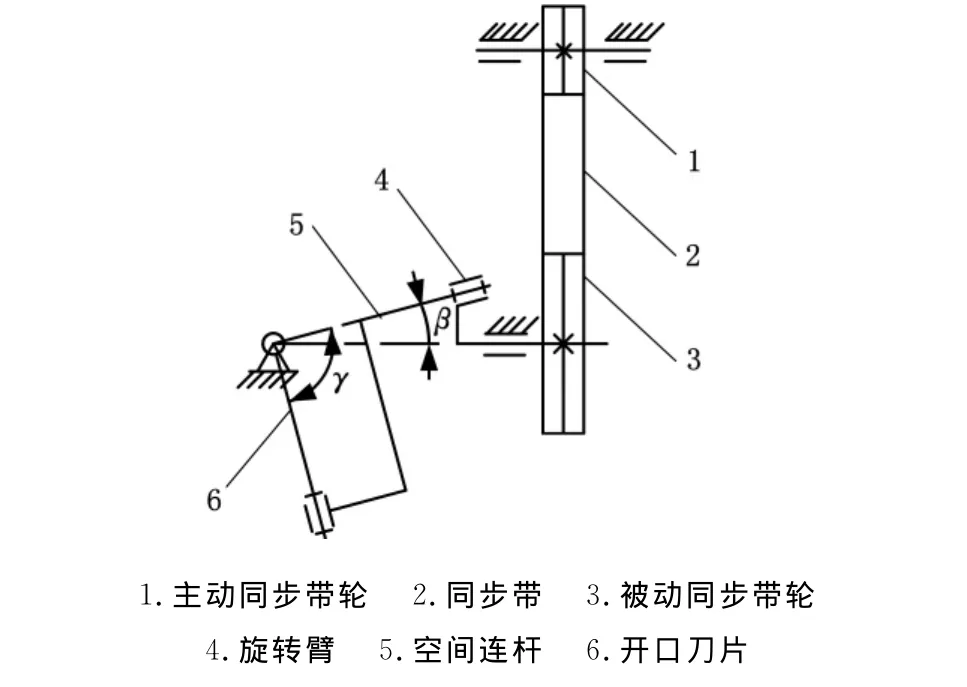
圖8 簡易開口機構驅動原理圖

5 結束語

本文所討論的球面4R機構，雖然只有2個結構參數γ和β，但通過選擇合適的γ和β可產生不同的位移、速度、加速度曲線，來滿足劍桿織機引緯空動程與總動程比值的不同要求。針對不同的目標函數如何選擇最優的γ和β的匹配還有待進一步的研究。通過選擇特殊的γ值，球面4R機構還能能應用到織機的開口部件中，作為開口驅動機構。

［1］陳建能，趙雄，徐賓，等.橢圓齒輪－曲柄搖桿引緯機構的運動學建模與特性分析［J］.中國機械工程，2007，18（19）：2294－2297.

［2］滕兵.織機引緯機構的分析研究［J］.紡織機械，2008（5）：46－48.

［3］苗鴻賓，喬峰麗.空間RSSR機構的運動分析和研究［J］.機械設計與制造，2008（2）：7－9.

［4］李克讓，陳明.劍桿引緯機構的傳動規律研究［J］.紡織學報，2004，25（1）：44－45.

［5］SommerⅢ H J.Jerk Analysis and Axode Geometry of Spatial Linkage［J］.Journal of Mechanical Design，2008，130（4）：042301.

［6］張啟先.空間機構的分析與綜合（上冊）［M］.北京：機械工業出版社，1984.

Kinematics Characteristics Research of Spherical 4R Mechanism and Its Application Explore

Zhou Xiangqin
Zhejiang Sci－Tech University，Hangzhou，310018

In order to apply spherical 4R mechanism to meet various reciprocating movements，based on spherical 4R weft insertion mechanism of GTM rapier loom，an output kinematics function of mechanism was established.Some important properties of kinematics function were proved with mathematic method，and the mapping between structure parameters and appearance of kinematics function curve was built.After creative design some structural parameters，some different appearances of kinematics function curve were obtained and the mechanism was changed.This changed mechanism can be used in designing weft mechanism and shed mechanism.The results indicate that many kind of applications can be obtained by reasonably combining two structure parameters in spherical 4R mechanism.

spherical 4R mechanism；kinematics characteristic；curve appearance；rapier loom；weft insertion

TH112.1

1004—132X（2011）02—0153—06

2010—04—09

國家科技支撐計劃資助項目（2009BAF39B00）；浙江省重點科技創新團隊項目（2009R50018）

（編輯 張 洋）

周香琴，女，1965年生。浙江理工大學機械與自動控制學院高級工程師。研究方向為劍桿織機和機構學。發表論文9篇。