四輥軋機輥系非線性參激耦合振動特性研究

劉浩然 時培明 陳 浩 侯東曉

燕山大學,秦皇島,066004

四輥軋機輥系非線性參激耦合振動特性研究

劉浩然 時培明 陳 浩 侯東曉

燕山大學,秦皇島,066004

考慮上下工作輥之間以及上下支撐輥與機架之間的非線性剛度和非線性阻尼,建立了四輥軋機輥系四自由度參激垂直耦合振動模型。運用多尺度法求解了該系統在主共振和1∶1內共振情形下的解析近似解,得到了幅頻特性曲線方程。分析了軋機主要參數對主共振的影響,通過分析1∶1內共振幅頻特性曲線,發現內共振和主共振一樣存在幅值跳躍現象。通過數值仿真驗證了模型及分析結果的有效性,并分析了參激耦合振動系統隨參數變化時的局部分岔現象。研究結果可為軋機輥系垂直顫振機理分析及抑制提供參考。

軋機;參激振動;穩定性;內共振

0 引言

隨著現代化工業的快速發展,各行各業對鋼材的需求量不斷增大,同時對其質量的要求也越來越高。然而,軋制過程中時常發生的顫振現象,不僅會導致軋件厚度波動,使軋件表面產生明暗條紋,影響產品質量,嚴重時可能導致軋機設備的損壞,尤其是對薄規格帶鋼產品質量的影響突出。因此,長期以來許多科研人員致力于軋機顫振理論的研究以揭示其產生機理,掌握其規律,從而加以消除和抑制[1]。

軋機輥系垂直顫振的研究一直是科研工作人員關注的重要課題。Yarita等[2]將軋機按上下輥系簡化為兩自由度線性垂振系統,通過分析輥系間剛度的簡諧波動,研究了線性參激共振現象,并給出了參激共振的穩定判別式;Wiatoniow ski等[3]建立了四自由度的線性直串垂振系統,分析了參數的變化對產品質量的影響。然而只考慮線性因素無法解釋軋機實際運行中出現的復雜振動現象,并且把工作輥和支撐輥看作一體來進行研究,將忽略工作輥與支撐輥之間的振動現象。

軋機輥系存在著眾多的非線性參數因素,這些因素與輥系垂直顫振密切相關。軋機輥系顫振主要表現在工作輥和支撐輥與機架間的相對運動上,受軋件及輥系間的非線性參數影響尤為明顯。本文在考慮軋制界面間的非線性阻尼以及輥系間的非線性剛度的基礎上,建立了四輥軋機輥系四自由度非線性參激耦合振動模型。采用多尺度法求解了該非線性系統參數的主共振和1∶1內共振情況下的解析近似解,導出了系統的幅頻特性方程。通過仿真分析了軋機不同參數對主共振和內共振的影響,發現內共振同樣存在幅值跳躍現象。采用數值法驗證了該模型的有效性,為實際生產中解決這類軋機振動問題提供了一定的理論參考。

1 四輥軋機輥系非線性參激耦合振動模型

由于軋機非線性振動的復雜性,在簡化非線性參數上,非線性剛度和非線性阻尼項通常是在線性剛度和線性阻尼上加一個微小變化量來體現,其中非線性剛度和非線性阻尼微量廣泛采用的duffing()振子和van der pol()振子的形式,已經在工程界得到了廣泛的應用和認可,并且在軋機非線性振動研究中取得了較好的分析結果[4-6]。本文分別采用Duffing振子和 van der po l振子來描述非線性剛度和非線性阻尼項。

軋機輥系系統的垂直振動按研究內容的側重點不同,可采用不同的簡化模型,本文為了全面分析軋機輥系工作輥及支持輥的非線性參數激勵振動情況,建立了一個新的四輥振動模型,非線性項主要考慮上支撐輥與機架、上工作輥與下工作輥之間和下支撐輥與底座之間的非線性作用。下面主要進行參激耦合振動分析,為這類振動現象給出合理的解釋,以便進行振動的消除及抑制。四輥軋機輥系四自由度垂直非線性參激振動模型如圖1所示。其中m1和m2分別為工作輥和支撐輥的質量,k1和k3分別為機架與支撐輥和工作輥間的非線性彈性剛度系數;k2和k4分別為機架與支撐輥和工作輥間的線性彈性剛度系數;k0為工作輥間的線性彈性剛度;c1和c3分別為機架與支撐輥和工作輥間的線性阻尼系數;c2和c4分別為機架與支撐輥和工作輥間的非線性阻尼系數。E cos(υt)表示軋制過程中的外部激勵。

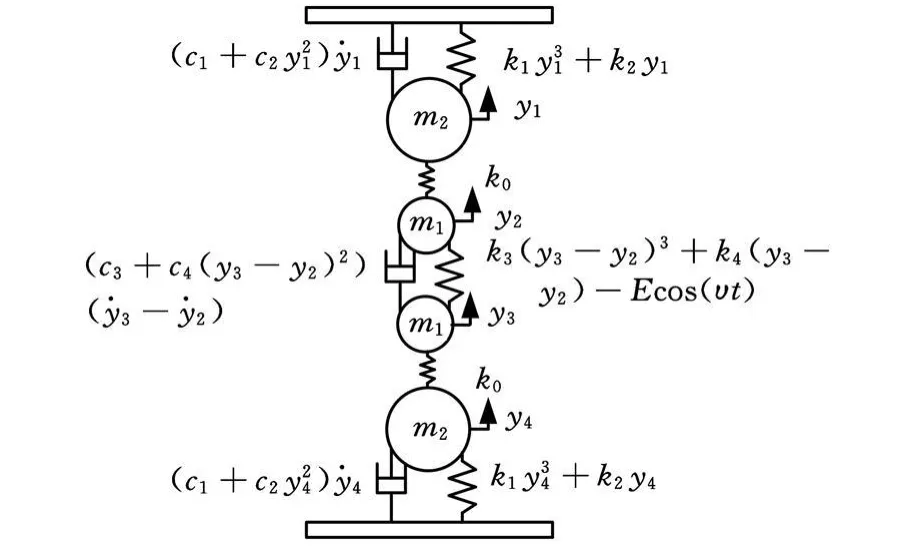
圖1 四輥軋機輥系非線性參激振動模型

因此,四輥軋機的非線性參激振動方程可表示為

2 四輥軋機輥系非線性參激耦合振動求解

在軋制過程中,輥系內部存在著復雜的參激振動。采用多尺度法進行參數共振分析[9],假設ε為小參數,當系統存在共振時,激勵頻率υ接近系統的固有頻率ω,有

2.1 主共振求解

2.2 內共振分析

當外部激勵為某一特殊頻率時,會引起軋機工作輥與支撐輥組成的振動系統的內部共振。

假設頻率滿足ω1=ω2-εδ,υ=ω1+εδ,代入式(8),并消去久期項得到

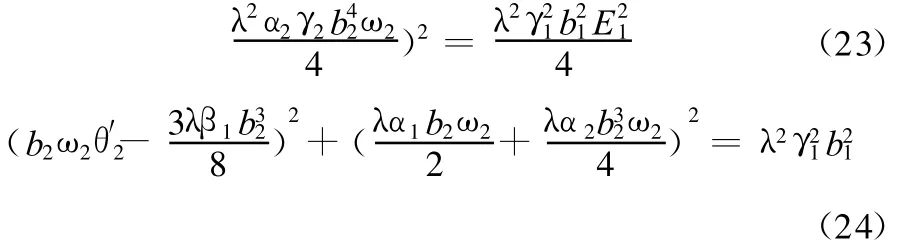
3 數值仿真

仿真實例的參數是將實際物理參數通過第1部分的標幺化處理后得到,與某廠1780軋機機架輥系參數基本一致。這些參數主要分為線性和非線性參數兩部分,其中,ω1和 ω2是標幺化后的線性剛度系數;α1和α3是標幺化后的阻尼系數;非線性阻尼系數 α2、α4和非線性剛度系數 β1、β2的測試比較困難,主要參考文獻[4]進行選取,其取值分 別 為:α1=0.06,α2=0.03,α3=0.05,α4=0.02,β1=0.02,β2=0.03,γ1=0.1,γ2=0.2,ω1=1.2,ω2=1.199。

圖2為主共振非線性剛度變化時的幅頻特性曲線圖,由圖2可見,隨著β2(非線性剛度)的增大,系統的頻響曲線向右偏移,并且逐漸出現跳躍區域(圖中虛線之間的部分)。從圖2中可以看到,擾動頻率從負到正變化時,幅值會按著1-2-3-5的路線變化,在3-5處形成幅值的跳躍,引起系統的振蕩。擾動頻率從正向負變化時,幅值會按照5-4-2的路線變化,在4-2形成幅值的跳躍,引起系統的振蕩。

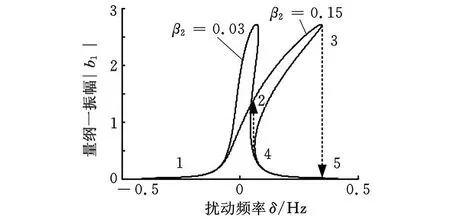
圖2 主共振非線性剛度變化時的幅頻特性曲線

圖3為主共振時阻尼變化時的幅頻特性曲線圖,由圖3a可見,隨著α1(線性阻尼)的增大,系統的振幅相應減小。由圖3b可見,隨著α2(非線性阻尼)的增大,系統的振幅減小,但非線性阻尼的影響程度要小于線性阻尼的影響程度。

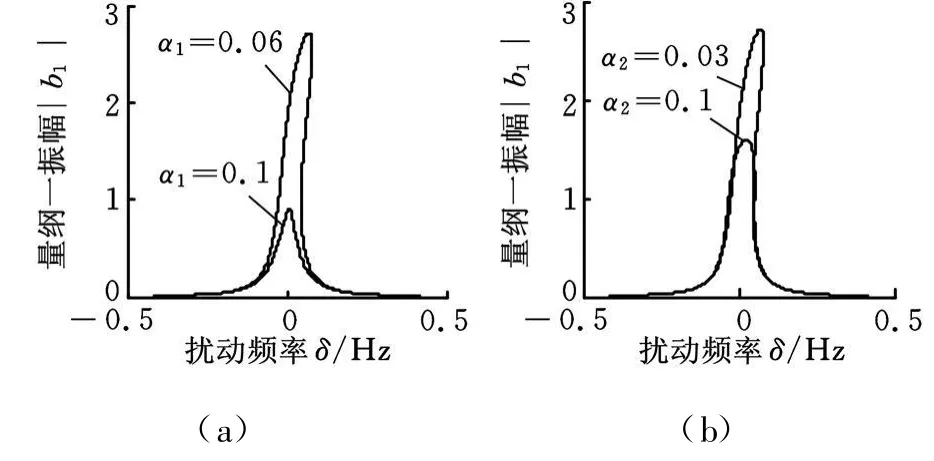
圖3 主共振時阻尼變化時的幅頻特性曲線

圖4為在外激力E1=0.05下的1∶1內共振幅頻曲線圖,從圖中可以看出隨著擾動頻率從小到大的變化,耦合系統有兩個共振點不存在跳躍現象,此時系統的解唯一存在且是穩定的。

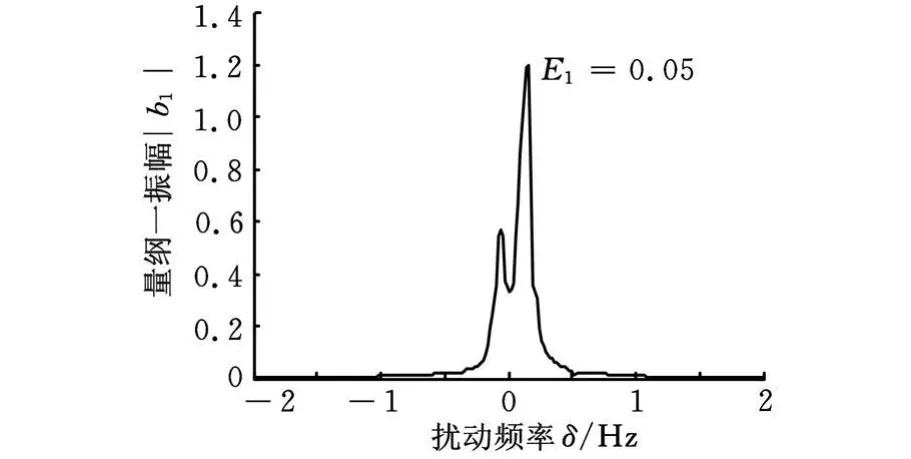
圖4 內共振幅頻特性曲線

圖5為在外激力E1=0.5下的1∶1內共振幅頻曲線圖,從圖中可以看出隨著外激勵的增大,曲線逐漸出現了彎曲,相應地表現出了跳躍現象,其中有一部分曲線彎曲較快,說明耦合項對其影響較大。

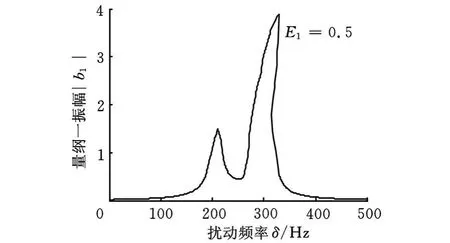
圖5 內共振幅頻特性曲線

圖6為工作輥與支撐輥振動的數值仿真曲線圖,從圖中可以看出虛線(支撐輥振動曲線)要滯后于實線(工作輥振動曲線),說明工作輥與支撐輥的振動情況并非完全一致,表明把工作輥和支撐輥分開研究更具現實意義。

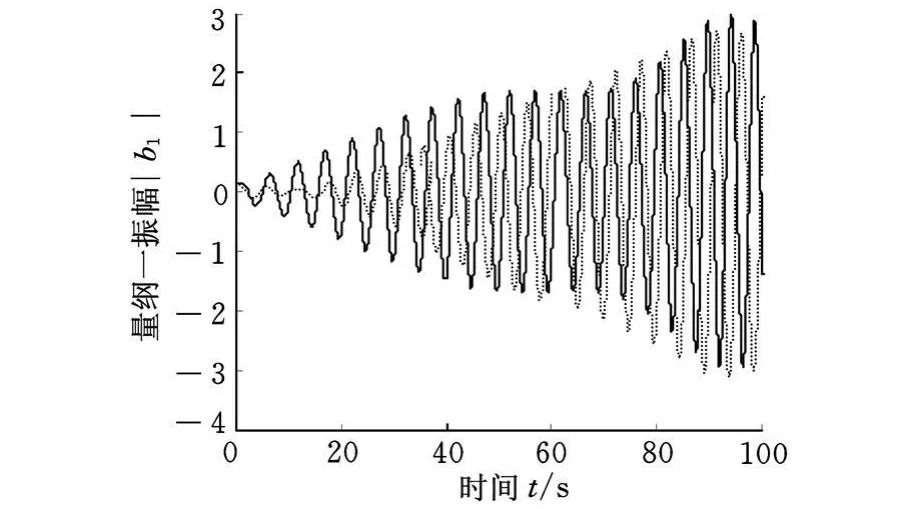
圖6 工作輥和支撐輥振動曲線

圖7為軋機工作輥與支撐輥的龐加萊截面圖,從圖中可以看出由于外激勵的影響,系統發生了振動現象,最后達到穩定的極限環,對應輥系的顫振自激振動。

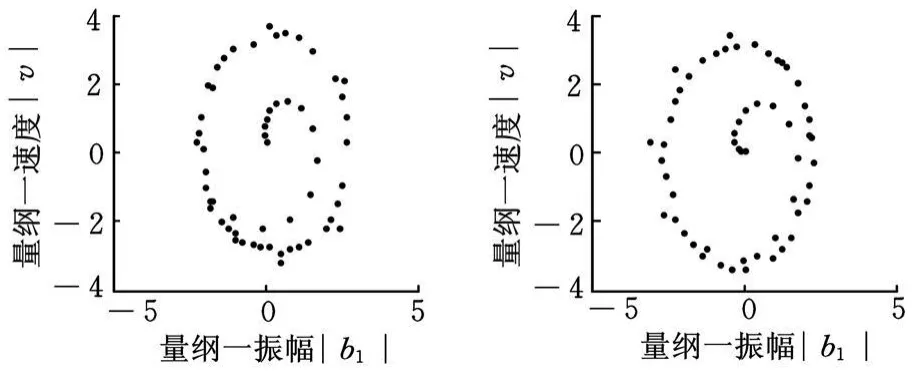
圖7 工作輥和支撐輥振動龐加萊截面

圖8為隨著參數E1變化的參激振動系統的分岔圖,從圖中可以看出隨著外激勵的增大,系統出現了分岔現象,E1從0.05系統開始發生分岔,到0.64系統又回到穩定狀態。

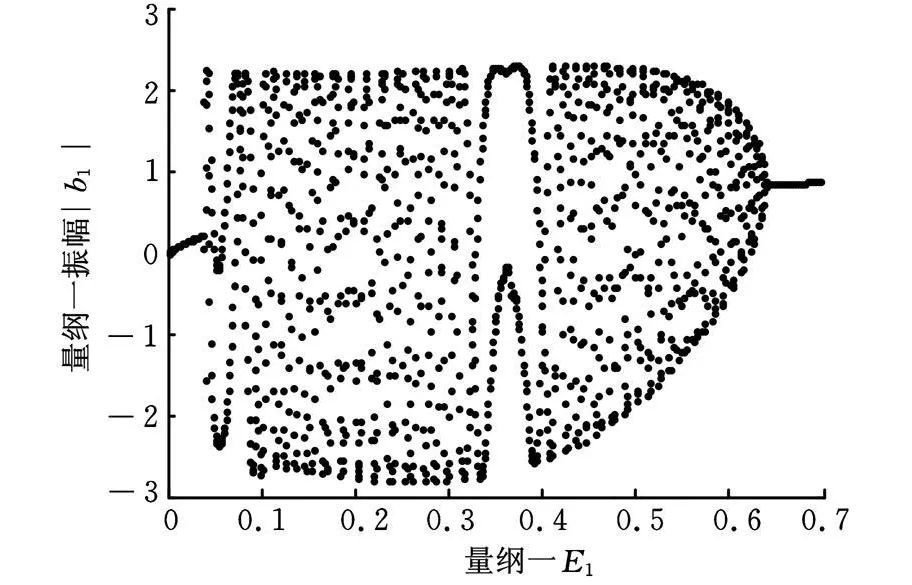
圖8 參激振動耦合系統隨控制參數E1變化的分岔特性

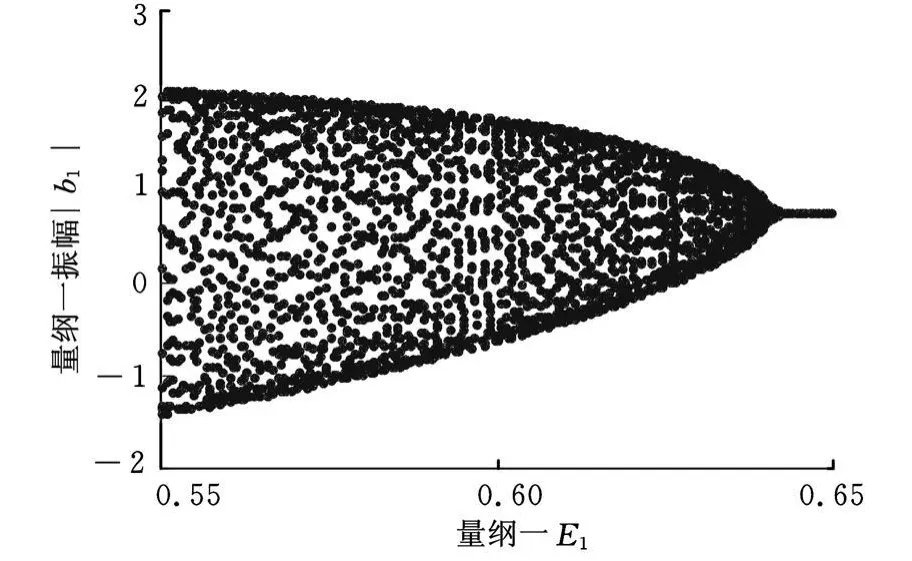
圖9 參激振動耦合系統的局部分岔圖

圖9為參激振動耦合系統的局部分岔圖,圖中對系統的分岔現象進行了細化,從其中可以看出在E1=0.64時系統漸變穩定,因此,可以通過改變系統參數及激勵參數來實現軋機輥系振動的抑制。圖10、圖11為不同參激參數E1下軋輥振動時時域曲線圖。其中圖10為參激參數E1=0.3時軋機振動曲線,此時振動表現為非周期運動,其振動最大幅值達到了3;圖11為參激參數E1=0.64時軋機振動曲線,此時為穩定的周期振動,其振動幅值為2。由圖10、圖 11可見,在不同的參激參數下,軋機的最大振動幅值有所不同,因此通過選取合適的參激振動參數有助于減小軋機的振動幅值。

4 結語

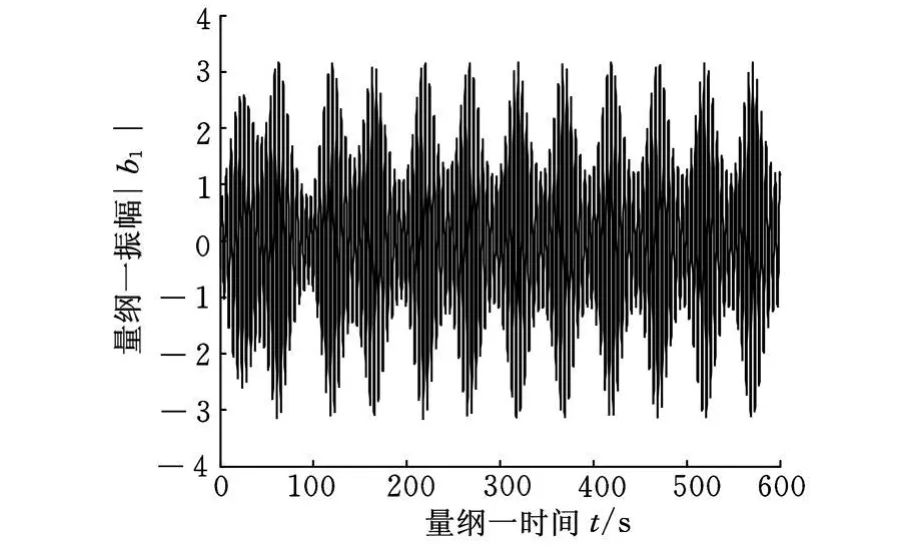
圖10 E1=0.3時軋輥振動時域曲線

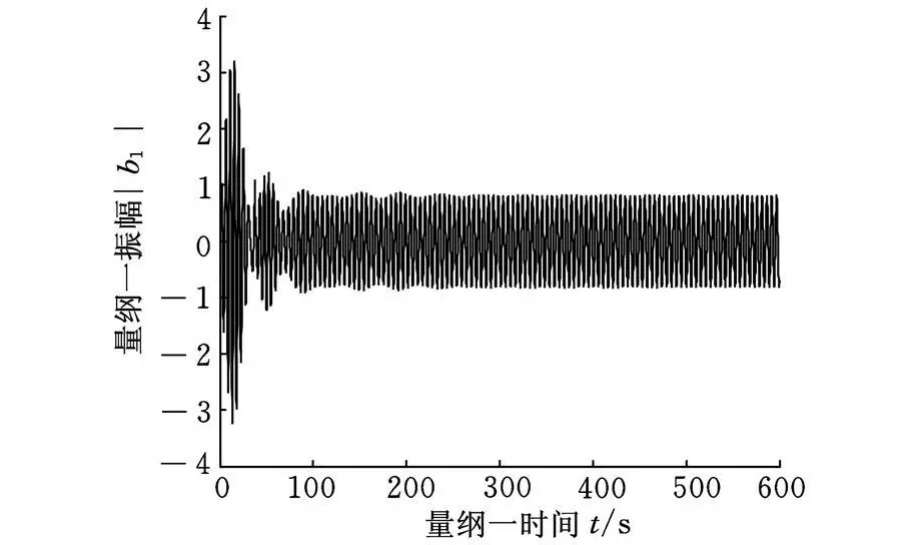
圖11 E1=0.64時軋輥振動時域曲線

本文考慮上下工作輥之間以及上下支撐輥與機架之間的非線性剛度和非線性阻尼,建立了四輥軋機輥系非線性參激耦合振動模型。采用多尺度法求解了該模型的主共振和系統的1∶1內共振響應,導出了系統的幅頻特性方程。通過仿真分析了軋機不同主參數對主共振的影響,分析了主共振和內共振幅頻特性規律,分析了耦合參激振動系統隨參數變化時的局部分岔現象。通過數值仿真驗證了模型及分析結果的有效性,為軋機輥系垂直顫振機理分析及抑制提供了參考。

[1] Younes M A,Shahtout M,Dam ir M A.A Parameters Design Approach to Imp rove Product Quality and Equipment Performance in Hot Rolling[J].Journal of Materials Processing Technology,2006,171:83-92.

[2] Yarita I,Furukawa K,Seino Y.An Analysis of Chattering in Co ld Rolling of U ltrathin Gauge Steel Strip[J].Transac tions ISU,1979,19(1):1-10.

[3] W iatoniow ski A S,Bar A.Parametrical Excitement Vibration in Tandem M ills-mathematical Model and Its Analysis[J].Journalof Materials Processing Technology,2003,134:214-224.

[4] 陳勇輝,史鐵林,楊叔子.四輥冷帶軋機非線性參激振動的研究[J].機械工程學報,2003,39(4):56-60.

[5] 孟令啟,杜勇,馬生彪,等.中厚板軋機垂直振動的非線性[J].吉林大學學報,2009,39(3):712-715.

[6] 杜勇,孟令啟,郭斌,等.立輥軋機主傳動系統的非線性參激振動仿真[J].鄭州大學學報,2009,41(3):109-113.

[7] Hu Peihua,Ehmann K F.Stability Analysis o f Chatter on a Tandem Rolling M ill[J].Journal of Manufac turing Processes,2000,2:217-224.

[8] 時培明,劉彬,劉爽.一類諧波激勵相對轉動非線性動力系統的穩定性與近似解[J].物理學報,2008,57(8):4675-4685.

[9] 楊志安,趙雪娟,席曉燕.非線性彈性地基上矩形薄板的非線性振動與奇異性分析[J].振動與沖擊,2006,25(5):69-73.

Study on Nonlinear Parametrically Exited Coup ling Vibrations of Roller System on 4-H Rolling M ills

Liu Haoran Shi Peiming Chen H ao Hou Dongxiao
Yanshan University,Qinhuangdao,H ebei,066004

A vertical nonlinear parametrically exited coup ling vibration model o f 4-h ro lling system was established,which considered the nonlinear dam ping and non linear stiffness between w orking rolls and supporting ro lls to ro lling mill's frame,The parse app roxim ation so lution were carried out by using multiple-scalem ethod,undermain frequency,1∶1 inner resonance,and the curve equations of am plitude-frequency were obtained.The vibration characteristics of the system under nonlinear stiffness and nonlinear damping were analyzed.W ith the changesof nonlinear stiffness,the amp litude appears the jumping phenomenon.It leads instability of the system.The numerical simulation indicates that the solution is validated.Local bifurcation was studied w ith parameter transform.It can offer som e theoretic guidance on vibration mechanism and control in rollingm ills.

rollingm ill;parametrically exited vibration;stability;inner resonance vibration

O322;O323

1004—132X(2011)12—1397—05

2010—08—12

國家自然科學基金資助項目(51005196);河北省自然科學基金資助項目(E2011203069,F2010001317)

(編輯 何成根)

劉浩然,男,1980年生。燕山大學信息科學與工程學院副教授。主要研究方向為軋機振動及抑制。發表論文8篇。時培明,男,1979年生。燕山大學電氣工程學院講師。陳 浩,男,1984年生。燕山大學電氣工程學院碩士研究生。侯東曉,男,1982年生。燕山大學電氣工程學院博士研究生。