基于SONS的結構模態參數識別研究

劉曉偉 李舜酩 張袁元

南京航空航天大學,南京,210016

基于SONS的結構模態參數識別研究

劉曉偉 李舜酩 張袁元

南京航空航天大學,南京,210016

僅利用結構的振動響應信號,提出了使用2階非平穩源(SONS)盲分離方法識別結構模態參數的方法。在介紹SONS算法和采用盲源分離方法識別模態參數流程的基礎上,以簡支梁錘擊振動響應信號進行了實驗,并分析了響應信號含噪聲的情況。實驗表明,SONS方法準確地提取了簡支梁結構的低階模態振型、固有頻率和阻尼比,抗噪性能好,且分離結果較二階盲辨識(SOBI)算法準確、穩定。針對高階模態直接盲分離識別效果不好的現象,采用先濾波再盲源分離的方法,成功識別了高階模態固有頻率。

響應信號;模態參數;盲源分離;錘擊信號;信噪比

0 引言

盲源分離(blind source separation,BSS)僅從傳感器觀測信號中分離出源信號,具有其他分離方法無法比擬的優勢,是一種很有應用前景的信號處理技術。自Jutten等[1]提出了一種類神經盲源分離,即現在常稱的H-J算法以來,人們在盲源分離方面做了很多研究。近年來,在振動信號處理中應用盲源分離技術的文獻越來越多[2],比如從復雜的混合信號中提取用于軸承診斷的信號[3]、從噪聲環境中提取航空發動機轉子振動信號[4]、內燃機振動信號的盲源分離[5]、混疊轉子振動信號的盲源分離[6]等。

傳統的線性模態分析是將位移矩陣分解為一個模態振型矩陣和一個模態坐標矩陣。模態坐標代表了結構基本的振動形式,模態振型則反映了系統響應中各個基本振動形式的參與量。時域模態參數的識別可以看做是一個盲源分離問題[2],混合矩陣提供了模態振型,盲源分離的信號則包含了各階模態的固有頻率和阻尼比信息。文獻[2,7-8]討論了應用 AMUSE(algorithm for mu ltip le unknow n signals ex traction)和二階盲辨識(second order blind identification,SOBI)方法在系統的模態參數識別中的應用,指出了SOBI方法具有良好的抗噪性。文獻[9]采用穩健的SOBI(R-SOBI)算法對四自由度的彈簧質量模型進行了分析,指出R-SOBI算法比SOBI算法具有更好的抗噪性。

本文采用二階非平穩源(second order nonsteady source,SONS)盲分離方法對結構的振動響應信號進行信號分離,得到振型矩陣,然后通過從分離得到的單自由度信號中提取頻率及阻尼比,從而得到結構的各階模態參數。

1 盲源分離的基本概念

盲源分離是指在源信號與混合通道參數均未知的條件下,僅通過傳感器觀測信號來估計源信號的一種信號處理方法。盲源分離的數學模型可表示為

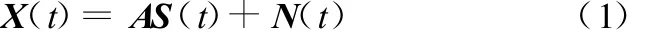
N個未知信號源Si(t)(i=1,2,…,N),構成一個列向量S(t)=(s1(t),s2(t),…,sN(t))T,t是離散時間。A是一個M ×N矩陣,稱為混合矩陣。N(t)=(n1(t),n2(t),…,nM(t))T是 M 維觀測高斯噪聲信號。而 X(t)=(x1(t),x2(t),…,xM(t))T則是通過傳感器觀察到的M維向量,通常情況下,假設噪聲是加性高斯噪聲。含有噪聲的盲源分離模型處理起來十分棘手,為簡單計,通常的研究不考慮噪聲的影響,其分離模型可表示為

式中,Y(t)為分離信號矢量(即源信號的一個估計值);W為N×M矩陣,稱為分離矩陣或解混矩陣。

由于混合系統的參數和源信號的先驗知識都是未知的,所以需要作如下假設:①各源信號之間相互統計獨立,且源信號之間最多只有一個高斯分布的源,否則不能分離;②觀測信號數大于或者等于源信號數,且混合矩陣為列滿秩矩陣。

在上述假設條件下,盲源信號分離的求解結果有不確定性,主要表現為分離后信號矢量的排列順序可以變化和信號的幅值與初始相位可以變化。但通常這并不影響源信號的識別,因為源信號的大多數有關信息都包含在其波形上,而不是在它們的幅值和排列次序上。

2 二階非平穩源盲分離算法

在SOBI算法中,白化矩陣是通過零時延協方差矩陣的特征分解求得,這不能有效降低噪聲的干擾,會影響算法的分離精度。SONS方法采用一種穩健的白化方法,即利用多個時延協方差矩陣生成一個線性混合矩陣,通過適當的參數選擇來保證該線性組合矩陣的正定性,進而對該矩陣進行奇異值分解來獲取相關的白化矩陣,并獲取白化信號。該白化算法是一個迭代運算過程,對加性噪聲的影響不再敏感。該方法按如下步驟來實現:

(1)計算觀測數據在不同時延τj下的協方差矩陣 CX(τj),并調整為

SONS算法步驟可以歸納為:①利用上述的穩健白化算法對觀測信號進行白化處理,得到白化信號Z(t);②將白化信號Z(t)劃分為互不重疊的K個數據塊,計算每個數據塊在不同時延下的協方差矩陣Mz(tk,τj);③將在 ②中得到的時延協方差矩陣進行聯合近似對角化,得到正交分離陣?U;④求取分離矩陣W=?UTQ。

從而可以得到源信號的估計:

3 模態參數識別基本概念

模態參數識別包括提取結構一系列的模態頻率、模態阻尼和模態振型。在這些參數中,模態振型以數學向量的形式描述了系統在某一模態頻率下的振動形式,它反映了系統振動從物理空間到模態空間的映射關系。

根據結構動力學理論,一個n自由度線性系統的自由振動方程為

模態參數識別的任務就是從結構的響應輸出x(t)中提取振型矩陣φ和包含在模態響應Q(t)中的模態頻率ωi及模態阻尼比ζi。從式(14)可以看到,時域的模態分析與盲源分離之間存在著一些相似之處,兩者都是從混合信號中估計潛在的組成分量;兩者都是僅僅利用結構系統的輸出信息。模態響應Q(t)相當于源信號S的一種特例。盲源分離主要是從混合信號中估計分離矩陣W=A-1,而這其中正包含有模態振型矩陣的信息,即φ=A。結構的模態頻率wi及模態阻尼比ζi可以從分離信號Q(t)中分析得到。盲源分離方法提取模態參數的流程圖如圖1所示。

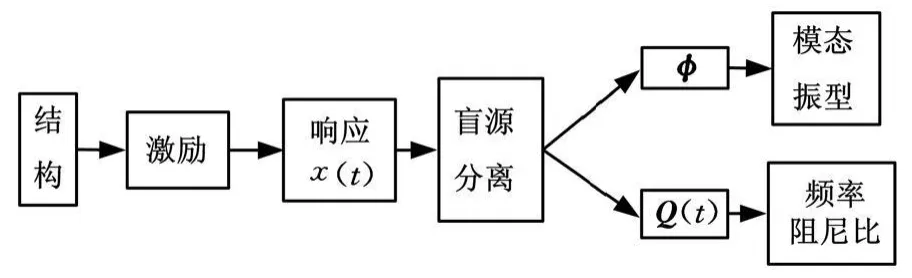
圖1 盲源分離提取模態參數流程

4 實驗研究

采用簡支梁模型對盲源分離提取模態參數進行實驗研究。簡支梁的前3階模態固有頻率分別為 102.54H z、288.09H z、563、96H z,前 3 階模態阻尼比為0.25%、1.45%、0.77%。對簡支梁施加垂向錘擊激勵,用6個加速度傳感器采集垂向響應信號,6個傳感器的采樣頻率均為5000H z,響應信號如圖2所示。

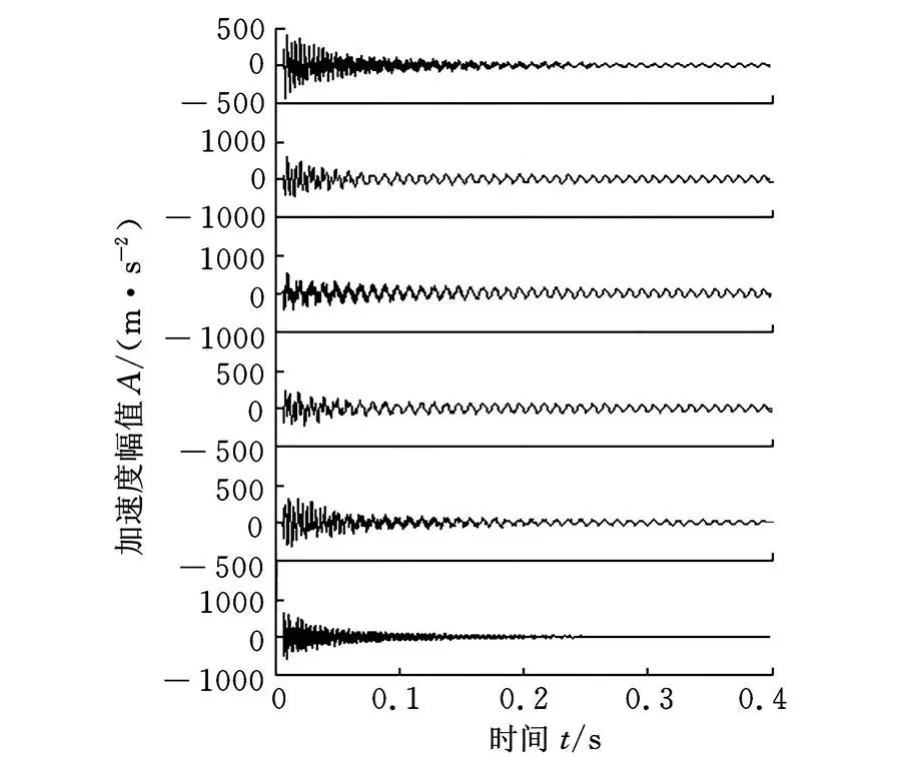
圖2 簡支梁錘擊響應信號

采用SONS方法對振動響應信號進行盲源分離,得到的各個時域信號即為模態坐標下的單自由度振動響應信號,如圖3所示。通過SONS算法所估計的各個分離信號的混合矩陣H就是模態振型矩陣,振型矩陣H的每一列都是一個振型向量,其階次與分離信號相對應。混合矩陣H為

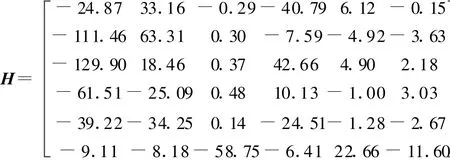
可以看出,通過盲源分離得到的振型矩陣能夠反映前6階振型的基本形狀。對分離得到的時域信號進行頻譜分析,就可以識別出各階模態的固有頻率,如圖4所示。從圖4可以看出,前3階模態坐標響應信號得到了很好的分離,高階模態坐標響應信號分離效果不好。

通過模態坐標下的單自由度響應信號,采用振幅對數衰減率的方法可以識別出各階模態的阻尼比。簡支梁前3階模態固有頻率、阻尼比識別結果見表1。表1中同時給出了SOBI(二階盲辨識)算法和模態實驗的結果。

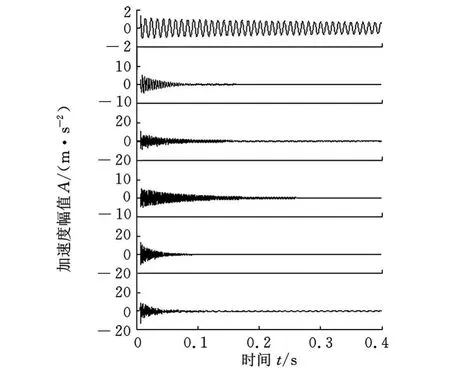
圖3 SONS算法振動響應分離信號

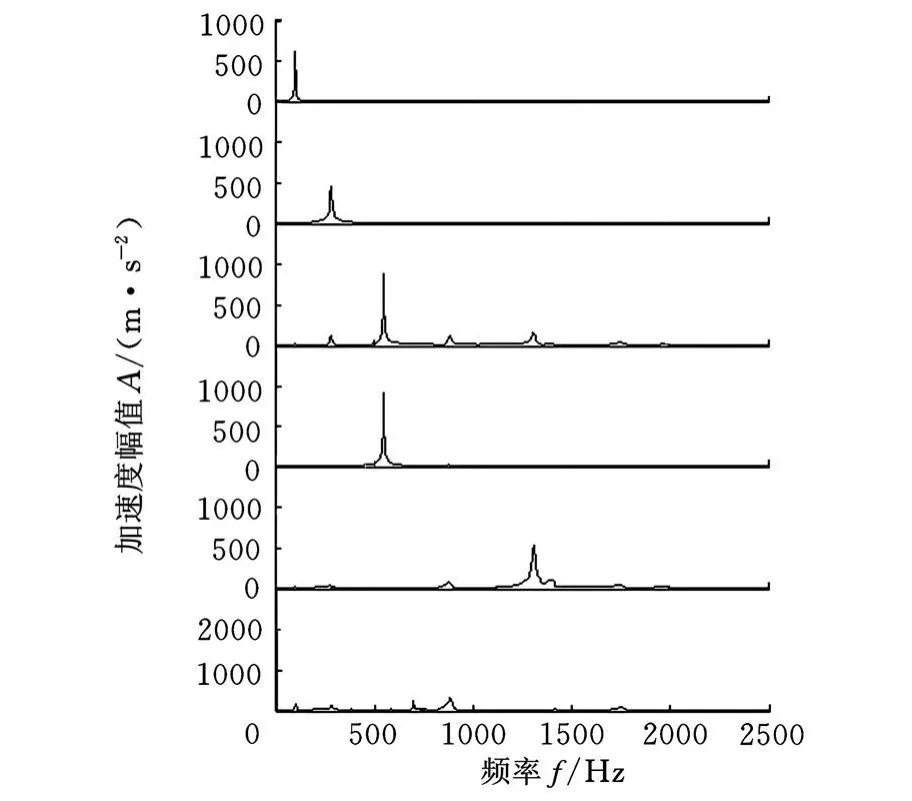
圖4 SONS算法振動響應分離信號頻譜

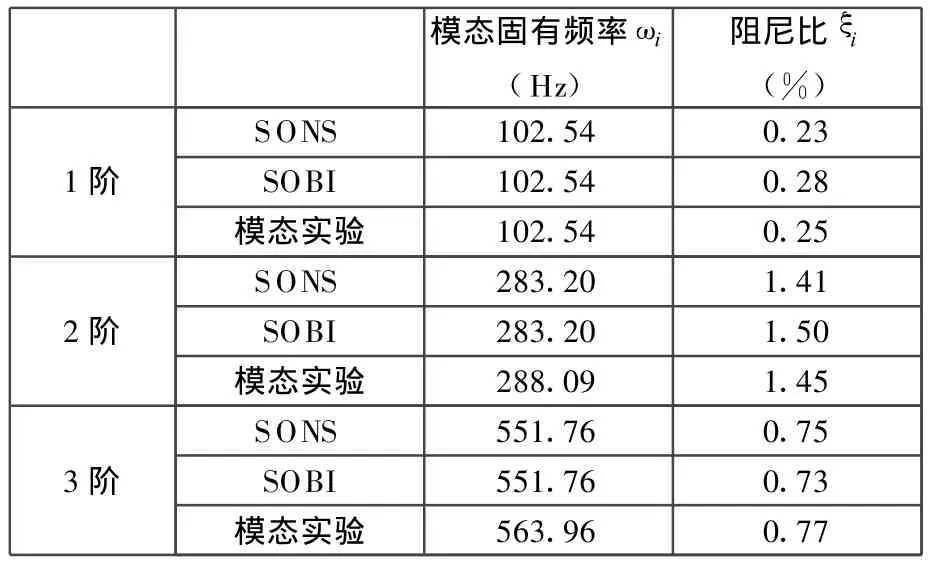
表1 盲源分離提取模態參數

從表1中可以看出,簡支梁結構前3階模態固有頻率和阻尼比都得到了準確的識別,SONS算法和 SOBI算法的識別結果差別不大,但SONS算法比SOBI算法識別的阻尼比更加準確。對采集的錘擊振動響應信號添加信噪比(SNR)為20dB的高斯白噪聲,采用SONS算法進行盲源分離,分離結果如圖5、圖6所示。

從圖5、圖6可以看到,分離信號的順序與未添加噪聲時不同,這是由盲源分離本身的特性所決定的,不影響我們通過分離信號識別模態參數。

從圖6可以看出,添加信噪比為20dB的高斯白噪聲之后,結構前3階的模態固有頻率仍然可以得到很好的識別,通過分離的時域信號可以提取模態阻尼。進一步增加噪聲強度,對錘擊響應信號分別添加信噪比為15dB、10dB和5dB的高斯白噪聲,進行盲源分離,并與SOBI分離結果進行對比,模態參數的識別結果見表2。

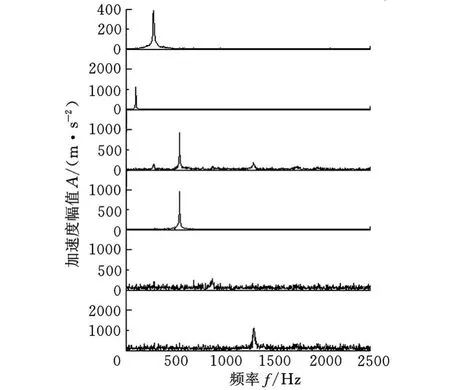
圖6 信噪比為20dB時響應信號的SONS分離信號頻譜

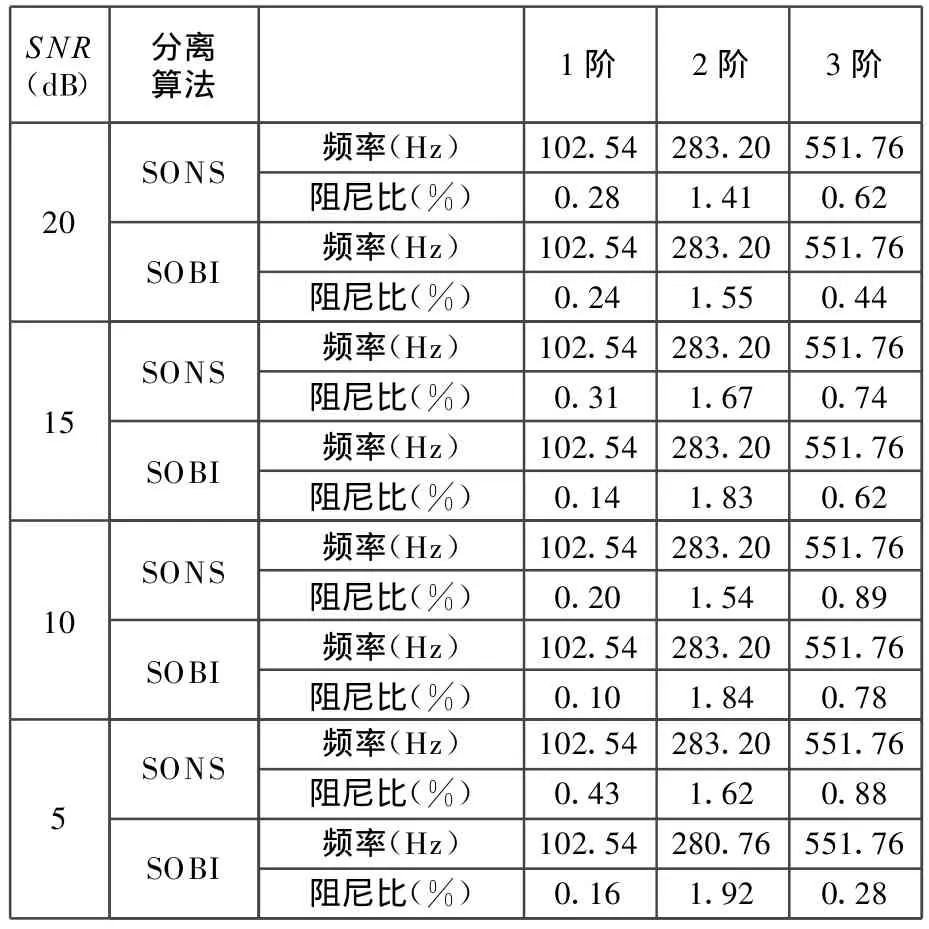
表2 不同信噪比下頻率、阻尼比識別結果

從表2中可以看出,對于含噪聲的信號,兩種方法對模態固有頻率的識別結果基本相同,但對阻尼比的識別,采用SONS方法的識別結果明顯要優于SOBI方法的識別結果,特別是在信噪比為5dB的強噪聲情況下。采用SOBI方法識別的阻尼比誤差很大,并且識別結果不穩定,而采用SONS方法得到的結果較準確,且穩定性好,可見SONS算法比SOBI算法具有更強的抗噪性。

對于高階的模態參數,由于分離出的時域信號受剩余模態的影響,阻尼比的識別受到限制,但模態固有頻率可采用先濾波再分離的方法進行識別。從圖 4可以看到,第4階模態固有頻率在886Hz左右,但其峰值較小,識別精度受到影響,因此可以濾掉800H z以下頻率的信號,然后再采用盲源分離的方法分離信號。分離信號的頻譜如圖7所示。

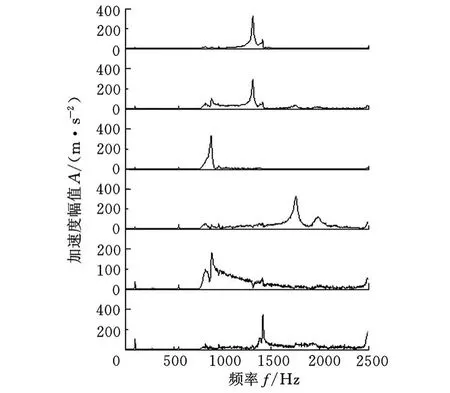
圖7 濾波后SONS分離信號頻譜

從圖7中可以很明顯地得到簡支梁第4階、第5階和第6階模態的固有頻率,分別為883.79Hz、1311.04H z、1755.37Hz,通過模態實驗得到的結果為 903.32H z、1346.26H z、1789.52Hz,可見通過先濾波再盲源分離的方法可以得到較準確的高階模態固有頻率。

5 結論

(1)直接采用SONS盲源分離算法就可以準確地識別振動結構的低階模態參數。

(2)SONS盲源分離算法較SOBI盲源分離算法對模態參數的識別更準確。

(3)SONS算法具有很好的抗噪性,在強噪聲環境下也能準確識別模態參數,且識別結果準確、穩定。

(4)對振動響應信號先濾波再進行盲源分離,可以準確識別高階模態固有頻率。

[1] Jutten C,Herault J.Blind Separation of Sources,Part I:an Adap tive A lgorithm Based on Neurom imetic A rchitecture[J].Signal Processing,1991,24:1-10.

[2] Zhou Wen liang,Chelidze D.Blind Source Separation Based Vibration Mode Identification[J].Mechanical System and Signal Processing,2007,21:3072-3087.[3] Zang C,Friswel M I,Im regun M.Structure Damage Detection Using Independent Component Analysis[J].Structure H ealth Monitoring,2004,3(1):69-83.

[4] 李舜酩.轉子振動故障信號的盲分離[J].航空動力學報,2005,20(5):751-756.

[5] 石林鎖,袁濤.內燃機振動信號的盲源分離方法試驗研究[J].內燃機學報,2007,25(5):463-468.

[6] 雷衍斌,李舜酩,郝青青.一種基于累積量的盲源分離新方法及其應用[J].中國機械工程,2010,21(7):787-792.

[7] Kem chen G,Ponce let F,Golinval J C.Physical Interpretation of Independent Component Analysis in Structural Dynam ics[J].Mechanical System and Signal Processing,2007,21:1561-1575.

[8] Poncelet F,Ke-ehen G,Golinval JC,et al.Output Only Modal Analysis Using Blind Source Separation Techniques[J].Mechanical System and Signal Processing,2007,21:2335-2358.

[9] 付志超,程偉,徐成.基于R—SOBI的結構模態參數辨識方法[J].振動與沖擊,2010,29(1):108-111.

A Study of Structure Modal Parameter Identification Based on Second Order Non-stationary Source Separation

Liu Xiaowei LiShunm ing Zhang Yuanyuan
Nanjing University o f Aeronautics&A stronautics,Nanjing,210016

A method of identifying the structure's m odal parameters by second order nonstationary source separation(SONS)arithm etic was proposed only using structure's vibration response signals.On the basis o f introducing the process of SONS algorithm and the steps of using BSSmethod to identify modal parameters,an experimentwas carried out using the hammering signals of sim ply supported beam,and the response signals w ith noise were analyzed.The experim ent demonstrates that the structure's low order mode shape,natural frequency and dam ping ratio are picked up by SONS method accurately.The SONS algorithm has good noise immunity,and its separation resu lts are better and more steady than SOBI(second order b lind identification)algorithm.Aiming at the phenomenon where high order modal parameters can not be identified very well using direct BSSmethod,amethod of doing BSS after signal filtering was proposed and high order natural frequency w as identified by thismethod successfully.

response signal;m odal parameter;blind source separation(BSS);hammering signal;signal-noise ratio(SNR)

TB123

1004—132X(2011)12—1454—05

2010—08—05

江蘇省研究生培養創新工程資助項目(CX10B_094Z)

(編輯 何成根)

劉曉偉,男,1987年生。南京航空航天大學能源與動力學院碩士研究生。研究方向為信號處理、振動與噪聲控制。李舜酩,男,1962年生。南京航空航天大學能源與動力學院教授、博士研究生導師。張袁元,男,1983年生。南京航空航天大學能源與動力學院博士研究生。