簡述考查學生數(shù)學猜想的幾種常見方式

●李樹臣 (沂南縣教育局 山東沂南 276300)

簡述考查學生數(shù)學猜想的幾種常見方式

●李樹臣 (沂南縣教育局 山東沂南 276300)

《全日制義務(wù)教育數(shù)學課程標準》(以下簡稱《標準》)非常強調(diào)對學生猜想能力的培養(yǎng)．例如，在“基本理念”中指出:“學生的數(shù)學學習內(nèi)容應(yīng)當是現(xiàn)實的、有意義的、富有挑戰(zhàn)性的，這些內(nèi)容要有利于學生主動地進行觀察、實驗、猜測、驗證、推理與交流等數(shù)學活動”;在“設(shè)計思路”中指出，“推理能力主要表現(xiàn)在:能通過觀察、實驗、歸納、類比等獲得數(shù)學猜想，并進一步尋求證據(jù)、給出證明或舉出反例”;在闡述課程目標時指出，讓學生“經(jīng)歷觀察、實驗、猜想、證明等數(shù)學活動過程，發(fā)展合情推理能力和初步的演繹推理能力，能有條理地、清晰地闡述自己的觀點”等等．由此可見，在數(shù)學教學中培養(yǎng)學生的數(shù)學猜想能力非常重要．可喜的是，最近幾年的數(shù)學中考命題者在這方面進行了有益而大膽的探索，試卷中出現(xiàn)了一些引導學生去猜想的題目．為此，筆者從2010年各地的中考試卷中選擇部分有代表性的題目進行分析，以供參考．

1 從算式的計算中，歸納猜想規(guī)律

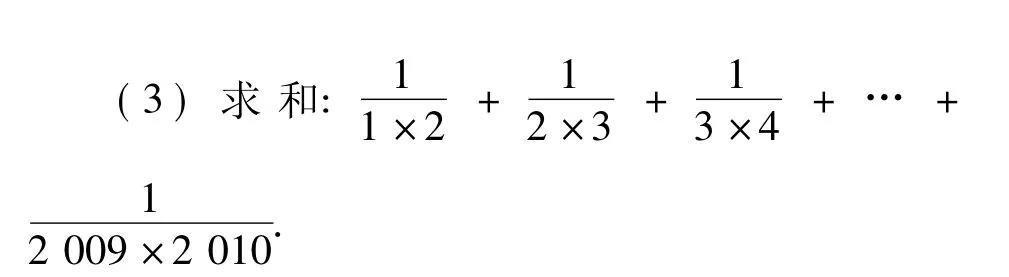
(2010年山東省濟寧市數(shù)學中考試題)

分析本題以簡單的分數(shù)計算為載體，以考查學生歸納猜想的能力為主．(1)觀察給定的3個等式，即可猜想得到結(jié)論;(2)根據(jù)分式加減運算法則通分計算;(3)根據(jù)第(1)小題的結(jié)果計算．

點評給定幾個代數(shù)計算式子，在計算的過程中通過歸納、猜想得到有關(guān)的規(guī)律，然后用代數(shù)變形的方式證明猜想的正確性，并利用猜想得到的規(guī)律解答給定的問題，這是一種常見的題型．解答這類問題需要有較強的觀察、分析、判斷、類比歸納等能力．在教學過程中，教師應(yīng)結(jié)合具體的教學內(nèi)容設(shè)計一些類似的題目讓學生去分析和思考，學生的歸納猜想能力必將得到較大的提高．

2 與數(shù)形結(jié)合思想聯(lián)系在一起，探索并猜想有關(guān)規(guī)律

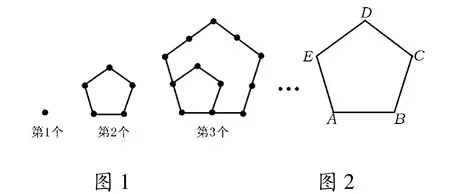
案例2 用棋子按下列方式擺圖形(如圖1所示)，依照此規(guī)律，第n個圖形比第n－1個圖形多＿＿枚棋子．

(2010年江蘇省徐州市數(shù)學中考試題)

分析本題創(chuàng)設(shè)了一個觀察棋子圖形中棋子個數(shù)的“數(shù)形結(jié)合”的數(shù)學模型．在解答時，需要從簡單到復雜進行探究:

第1個圖形顯然有1枚棋子;

第2個圖形有5枚棋子，它們分別在一個正五邊形的頂點處．為了便于分析，構(gòu)造正五邊形ABCDE，把五邊形一個頂點A看成是第1個圖形的一個點，這一點A是五邊形的邊AB和AE的交點．除這2條邊外，還有3條邊BC，CD，DE，每邊上有2個點，這樣還有3×2=6個點，但其中C，D這2個頂點計算了2次，應(yīng)減去，這樣就還有3×2－2=4個，即第2個圖形有1+3×2－2=5枚棋子．

第3個圖形比第2個圖形多一層五邊形，內(nèi)層五邊形就是第2個圖形，有5枚棋子．外層五邊形每邊上3枚棋子，類比第2個圖形，可計算第3個圖形中棋子的枚數(shù)為:5+3×3－2=12個．

同樣，第4個圖形中棋子的枚數(shù)為

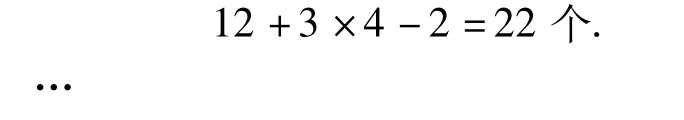
由此可以猜想得到規(guī)律:第n個圖形中棋子的枚數(shù)是第n－1個圖形中棋子的枚數(shù)加上3×n－2，這里3×n－2=3n－2就是增加數(shù)．

點評從分析的過程看，本題是借助于“圖形”的形象性與直觀性逐步得到解決的．除了考查學生的數(shù)學猜想能力外，還滲透了數(shù)形結(jié)合的思想．本題給我們的啟發(fā)有二:一是在數(shù)學學習中，當遇到一個問題涉及到很多或無窮多情形時，可以從問題的簡單情形或特殊情形入手，通過簡單情形或特殊情形的試驗，從中發(fā)現(xiàn)一般規(guī)律或作出某種猜想，從而找到解決問題的途徑;二是在教學中，千萬不要就知識點而講知識點，一定要把這些“顯知識”背后所“隱含”的數(shù)學思想揭示出來．做到用數(shù)學思想方法來“統(tǒng)領(lǐng)”知識點，以達到優(yōu)化知識結(jié)構(gòu)的目的，因為只有這樣被“優(yōu)化”起來的知識結(jié)構(gòu)才具有生命力和創(chuàng)造性．

3 從對簡單幾何體模型的觀察出發(fā)，猜想幾何體中有關(guān)元素之間的數(shù)字規(guī)律

案例3十八世紀瑞士數(shù)學家歐拉證明了簡單多面體頂點數(shù)(V)、面數(shù)(F)、棱數(shù)(E)之間存在的一個有趣的關(guān)系式，被稱為歐拉公式．請你觀察下列幾種簡單多面體模型(如圖3所示)，解答下列問題:

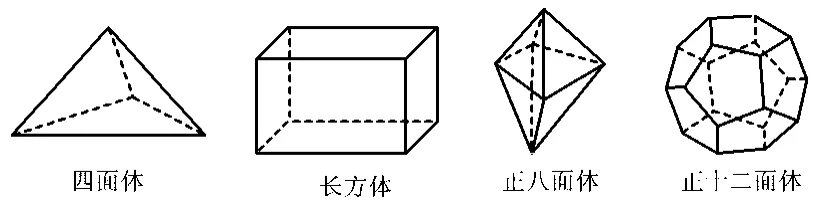
圖3

(1)根據(jù)上面多面體模型完成表1中的空格，可得出頂點數(shù)(V)、面數(shù)(F)、棱數(shù)(E)之間存在的一個有趣的關(guān)系式，如表1所示．

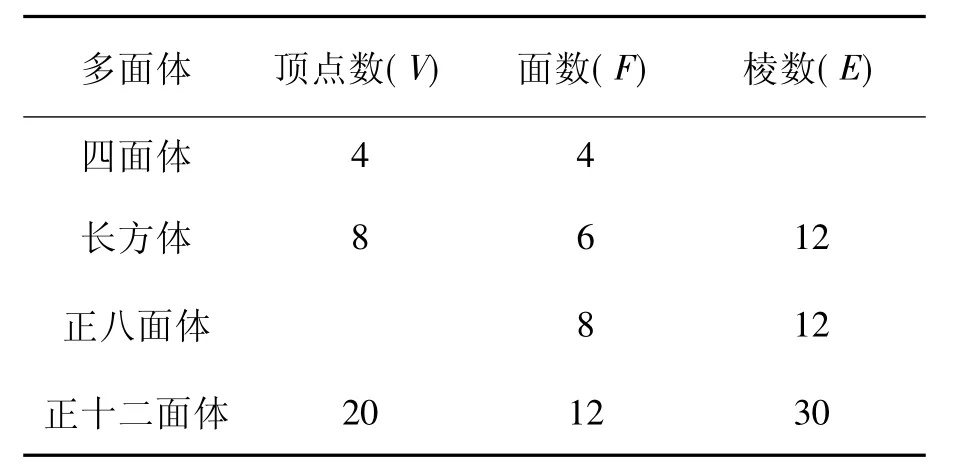
表1 頂點數(shù)(V)、面數(shù)(F)、棱數(shù)(E)的數(shù)值表

你發(fā)現(xiàn)頂點數(shù)(V)、面數(shù)(F)、棱數(shù)(E)之間存在的關(guān)系式是＿＿ ．

(2)一個多面體的面數(shù)比頂點數(shù)大8，且有30條棱，則這個多面體的面數(shù)是＿＿ ．

(3)某個玻璃飾品的外形是簡單多面體，它的外表面由三角形和八邊形這2種多邊形拼接而成，且有24個頂點，每個頂點處都有3條棱．設(shè)該多面體外表面三角形的個數(shù)為x，八邊形的個數(shù)為y，求x+y的值．

(2010年浙江省寧波市數(shù)學中考試題)

分析(1)仔細觀察給定的4個多面體模型，可知四面體的棱數(shù)為6，正八面體的頂點數(shù)為6;根據(jù)給定的4個多面體的頂點數(shù)(V)、面數(shù)(F)和棱數(shù)(E)之間的數(shù)量關(guān)系，可歸納、猜想得到它們之間的關(guān)系為V+F－E=2．(2)根據(jù)第(1)小題的結(jié)論求解．(3)多面體的面數(shù)為x+y，棱數(shù)為=36條．根據(jù)題意可列出一個方程，在求解時應(yīng)把x+y當作一個整體．

點評 歐拉是一位著名數(shù)學家，他淵博的知識、無窮無盡的創(chuàng)作精力和空前豐富的著作令世人驚嘆不已．本題的特點是給出幾個幾何體模型，讓學生觀察它們的頂點數(shù)、面數(shù)及棱數(shù)，為了啟發(fā)學生能獨立猜想到每個幾何體模型的這“3個數(shù)量”之間的關(guān)系，即猜想得到著名的歐拉公式．本題用圖表給出這些數(shù)中的大部分數(shù)，這樣可降低解題難度．學生一旦猜想到它們之間的關(guān)系，后面的問題就可以直接利用這一關(guān)系進行解答．

4 通過創(chuàng)設(shè)具體的問題情境、數(shù)學實驗等，考查學生數(shù)學猜想能力

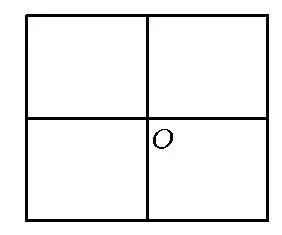
圖4

案例4 問題再現(xiàn)在現(xiàn)實生活中，鑲嵌圖案在地面、墻面乃至服裝面料設(shè)計中隨處可見．在八年級課題學習“平面圖形的鑲嵌”內(nèi)容時，對于單種多邊形的鑲嵌問題，主要研究了三角形、四邊形、正六邊形的鑲嵌．在此把正多邊形的鑲嵌作為研究問題的切入點，提出其中幾個問題來共同探究．

我們知道，可以單獨用正三角形、正方形或正六邊形鑲嵌平面．如圖4，若用正方形鑲嵌平面，則可以發(fā)現(xiàn)在一個頂點O周圍圍繞著4個正方形的內(nèi)角．

試想:若用正六邊形來鑲嵌平面，則在一個頂點周圍應(yīng)該圍繞著＿＿ 個正六邊形的內(nèi)角．

問題提出如果要同時用2種不同的正多邊形鑲嵌平面，那么能設(shè)計出幾種不同的組合方案?

問題解決 猜想1是否可以同時用正方形、正八邊形這2種正多邊形組合進行平面鑲嵌?

分析可以將此問題轉(zhuǎn)化為數(shù)學問題來解決．從平面圖形的鑲嵌中可以發(fā)現(xiàn)，解決問題的關(guān)鍵在于分析能同時用于完整鑲嵌平面的2種正多邊形的內(nèi)角特征．具體地說，就是在鑲嵌平面時，一個頂點周圍圍繞的各個正多邊形的內(nèi)角恰好拼成一個周角．

驗證1在鑲嵌平面時，設(shè)圍繞某一點有x個正方形和y個正八邊形的內(nèi)角可以拼成一個周角．根據(jù)題意得

結(jié)論1在鑲嵌平面時，在一個頂點周圍圍繞著1個正方形和2個正八邊形的內(nèi)角可以拼成一個周角，因此可同時用正方形和正八邊形這2種正多邊形組合進行平面鑲嵌．

猜想2是否可以同時用正三角形和正六邊形這2種正多邊形組合進行平面鑲嵌?若能，請按照上述方法進行驗證，并寫出所有可能的方案;若不能，請說明理由．

上面探究了同時用2種不同的正多邊形組合鑲嵌平面的部分情況，僅僅得到了一部分組合方案，相信同學們用同樣的方法，一定會找到其他可能的組合方案．

問題拓廣請你仿照上面的研究方式，探索出一個同時用3種不同的正多邊形組合進行平面鑲嵌的方案，并寫出驗證過程．

(2010年山東省青島市數(shù)學中考試題)

分析本題從日常生活中的“鑲嵌”問題出發(fā)，可分如下4個階段展開:問題再現(xiàn)——問題提出——問題解決——問題拓廣．

(1)在問題再現(xiàn)階段，要求學生觀察圖4，回答用正六邊形來鑲嵌平面，在一個頂點周圍應(yīng)該圍繞著幾個正六邊形的內(nèi)角?這非常簡單，學生都能類比猜想得到結(jié)論為3．

(2)提出問題:如果要同時用2種不同的正多邊形鑲嵌平面，那么能設(shè)計出幾種不同的組合方案?

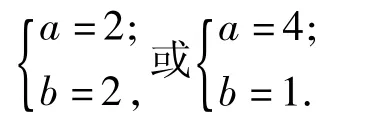
結(jié)論2在鑲嵌平面時，在一個頂點周圍圍繞著2個正三角形和2個正六邊形的內(nèi)角或者圍繞著4個正三角形和1個正六邊形的內(nèi)角可以拼成一個周角，因此可以同時用正三角形和正六邊形這2種正多邊形組合進行平面鑲嵌．

猜想3是否可以同時用正三角形、正方形和正六邊形這3種正多邊形組合進行平面鑲嵌?

驗證3在鑲嵌平面時，設(shè)圍繞某一點有m個正三角形、n個正方形和c個正六邊形的內(nèi)角可以拼成一個周角．根據(jù)題意得

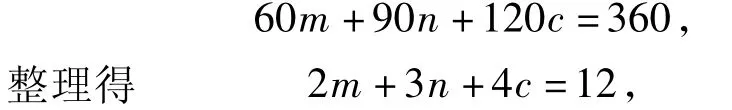
因此可找到惟一一組適合方程的正整數(shù)解為

(3)在問題解決階段給出了2個猜想，為了降低難度，題目對猜想1進行了分析和驗證并在得到結(jié)論1之后，提出了猜想2．對于這個猜想要求學生仿照對猜想1的驗證過程，對猜想2進行驗證，并歸納得出結(jié)論2．

(4)在問題拓廣階段，要求學生自己提出猜想、進行驗證、最后歸納出結(jié)論．

本題的特點是引導學生進行“閱讀—理解—猜想—驗證”，文字敘述較長，如果學生不認真進行分析，那么可能會無從下手．解答的關(guān)鍵在于仔細“審題”，理解題意．

驗證2在鑲嵌平面時，設(shè)圍繞某一點有a個正三角形和b個正六邊形的內(nèi)角可以拼成一個周角．根據(jù)題意得

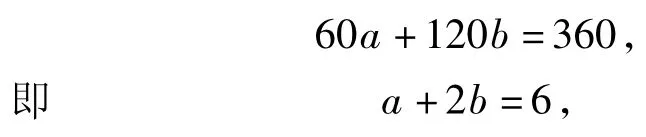
因此可找到2組適合方程的正整數(shù)解為

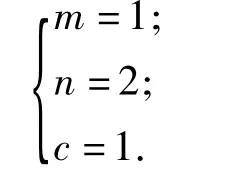
結(jié)論3在鑲嵌平面時，在一個頂點周圍圍繞著1個正三角形、2個正方形和1個正六邊形的內(nèi)角可以拼成一個周角，因此可以同時用正三角形、正方形和正六邊形這3種正多邊形組合進行平面鑲嵌(說明:本題答案不惟一，符合要求即可)．

點評近年來，各地中考卷中經(jīng)常出現(xiàn)這樣的問題:提供一個學生熟悉的生活材料，要求學生能夠從給出的問題情景中經(jīng)過分析找到解決問題的規(guī)律和方法，靈活運用有關(guān)知識加以解決．本題以學生熟悉的生活實際問題(鑲嵌)為背景，通過“再現(xiàn)生活中的實際問題——提出問題——問題解決——問題拓廣”，考查學生把能否“鑲嵌”的問題轉(zhuǎn)化為能否“拼成”一個周角的問題的能力，進而考查學生利用方程的知識解答問題的能力．解決這類問題需要有較強的閱讀理解能力和數(shù)學猜想能力，一般思路是:類比具體的范例猜想得到解題方法和規(guī)律，“模擬”此方法和規(guī)律解答類似相關(guān)問題．從深層看，本題以“鑲嵌”為背景，考查學生類比猜想、推理、論證的能力．

案例5 (1)操作發(fā)現(xiàn)如圖5，在矩形ABCD中，E是 AD的中點，將△ABE沿 BE折疊后得△GBE，且點G在矩形ABCD的內(nèi)部．小明將BG延長交DC于點F，認為GF=DF，你同意嗎?說明理由．

(2)問題解決保持第(1)小題中的條件不變，若 DC=2DF，求的值．

(3)類比探求 保持第(1)小題中條件不變，若 DC=n·DF，求的值．

(2010年河南省數(shù)學中考試題)

分析(1)在實驗操作時，只要能確定矩形ABCD的邊AD的中點E，按要求進行操作，將會發(fā)現(xiàn)GF=DF．仔細觀察發(fā)現(xiàn)，連結(jié)EF，得Rt△EGF≌Rt△EDF．只要能猜想到這一點，問題就容易解決了．(2)要求的值，只要求出即可．因為BF=BG+GF=AB+GF=DC+DF，而 DC=2DF，所以考慮到△BCF是直角三角形，利用勾股定理BC2+FC2=BF2，得BC與DC的關(guān)系，進而得解．(3)類比第(2)小題即可求解．

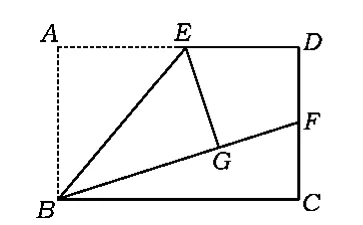
圖5

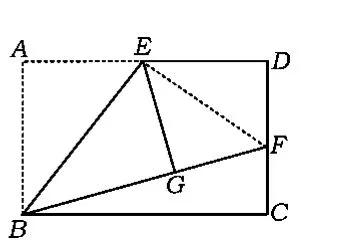
圖6

解(1)同意．如圖6，連結(jié)EF，則

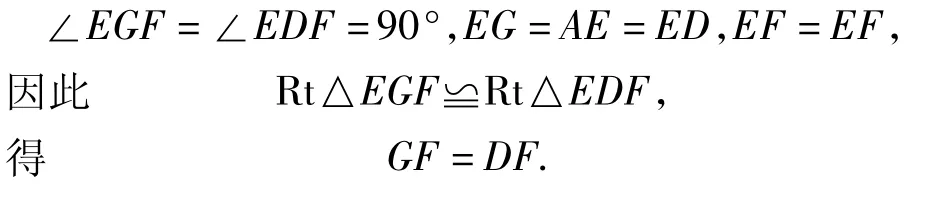
點評在最近幾年的中考試卷中，出現(xiàn)了一些讓學生通過“數(shù)學實驗——猜想結(jié)論——證明結(jié)論——利用結(jié)論”求解的題目，本題便是典型的一例．在實驗探究的過程中，能抓住變化中的等量關(guān)系，借助圖形的全等進行轉(zhuǎn)化是關(guān)鍵．這樣的題目對于培養(yǎng)學生的動手操作能力、猜想發(fā)現(xiàn)能力都是非常有益的．

總之，教師應(yīng)大力加強對《標準》和數(shù)學教科書的研究，精心設(shè)計教學，結(jié)合具體的教學內(nèi)容，努力把教學內(nèi)容設(shè)計成能引導學生進行觀察、實驗、分析、比較、聯(lián)想、類比、歸納的素材，以培養(yǎng)學生的數(shù)學猜想意識、猜想習慣、猜想能力，從而培養(yǎng)學生的創(chuàng)新能力．

［1］ 李樹臣．深入鉆研課程標準，努力創(chuàng)提問題情境［J］．中學數(shù)學，2009(2):1-3．

［2］ 李樹臣．淺談數(shù)學實驗的在教學中的應(yīng)用［J］．中國數(shù)學教育，2009(10):15-17．

［3］ 李樹臣．數(shù)學教學過程化的4個常用策略［J］．中國數(shù)學教育，2010(6):2-5．

［4］ 趙緒昌．數(shù)學猜想的理性認識與教學思考［J］．中學數(shù)學雜志，2010(8):1-2．