函數(shù)復(fù)合最值問題的常用求解策略

●高 召 (三門峽市第一高級(jí)中學(xué) 河南三門峽 472000)

函數(shù)復(fù)合最值問題的常用求解策略

●高 召 (三門峽市第一高級(jí)中學(xué) 河南三門峽 472000)

在數(shù)學(xué)競賽和高考題中，常常會(huì)遇到一些在一類最大值中求其最小值或在一類最小值中求其最大值的復(fù)合最值問題．它是函數(shù)最值問題中的一種特殊類型，解決這類問題的方法也比較特殊．本文介紹了解決此類問題的一些常用策略，供參考．

1 圖像法

例1用 min{a，b，c}表示 a，b，c這 3 個(gè)數(shù)中的最小值．設(shè) f(x)=min{2x，x+2，10 － x}(x≥0)，則f(x)的最大值為 ( )

A．4 B．5 C．6 D．7

(2009年寧夏、海南數(shù)學(xué)高考試題)

分析作出函數(shù)y=2x，y=x+2，y=10 － x的圖像，如圖1所示．由圖像可得，f(x)的解析式為

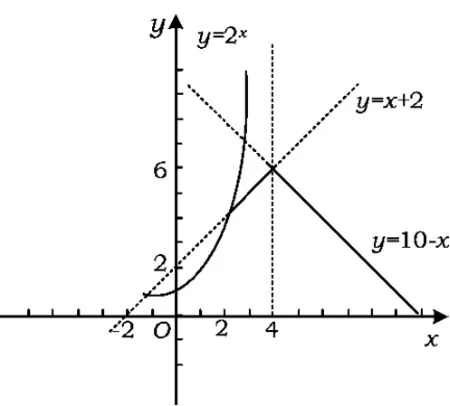
圖1

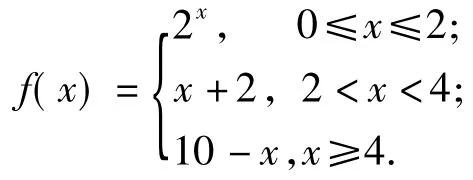
觀察f(x)圖像的最高點(diǎn)，得f(x)max=6．故選 C．

注對(duì)于涉及一元變量的多個(gè)函數(shù)的復(fù)合最值問題，采用圖像法求解會(huì)更加直觀、簡潔．

2 均值法

利用平均值是處理函數(shù)復(fù)合最值問題的最常用方法，往往選取算術(shù)平均值和幾何平均值進(jìn)行求解．若 M=max{x1，x2，…，xn}，m=min{x1，x2，…，xn}，設(shè) x1，x2，…，xn的算術(shù)平均值為 A，則 m≤A≤M．設(shè)正數(shù) x1，x2，…，xn的幾何平均值為 G，則 m≤G≤M．

注對(duì)于涉及多變量的復(fù)合最值問題，找出內(nèi)層最值與算術(shù)平均數(shù)或幾何平均數(shù)的不等關(guān)系，借助平均值不等式進(jìn)行轉(zhuǎn)化，是處理這類問題的常用方法．

3 設(shè)而不求法

對(duì)于雙層最值問題，可以先設(shè)出內(nèi)層最值，利用其最值性，建立關(guān)于內(nèi)層最值的不等式，然后通過解不等式的方法求出外層最值．

注(1)把內(nèi)層最值設(shè)出來，并不求出．如何利用已知條件尋找其滿足的不等關(guān)系是正確解題的關(guān)鍵．

(2)對(duì)于例3，可以借助柯西不等式直接建立內(nèi)層最值的不等式．

4 分類討論法

首先確定多個(gè)不同基本變量(自變量)的大小關(guān)系，然后利用各變量相等找出分類討論的分界點(diǎn)，再分類討論確定最值．

例4已知實(shí)數(shù)a，b，c滿足條件a+b+c=1，并且方程ax2+bx+c=0有實(shí)數(shù)根．記t=max{a，b，c}，求 t的最小值．

解(1)若 t=a，則

注通過討論基本變量的大小關(guān)系，可確定出內(nèi)層最值的表達(dá)式，再利用已知條件就能夠求出外層最值．

5 賦值法

通過對(duì)函數(shù)的主變量賦予特殊函數(shù)值得到第二類參變量滿足的不等式，再利用放縮法得到上界或下界，然后指出所得的界是能夠取到的．

注對(duì)于內(nèi)層函數(shù)含有絕對(duì)值符號(hào)的問題，常采用賦值放縮法進(jìn)行求解．

6 猜想反證法

對(duì)一些復(fù)合最值問題，可根據(jù)問題的極端情況先猜出最值，然后給出證明．如果從正面不好證明，那么可以考慮用反證法解．

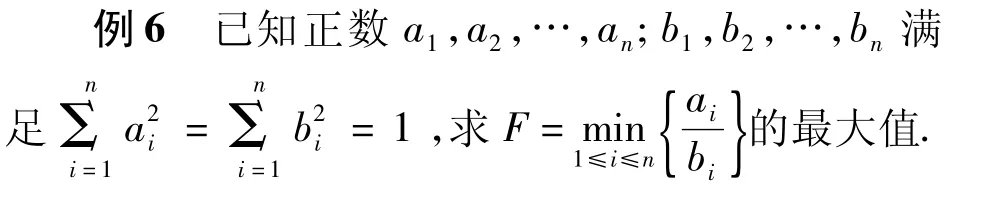
［1］ 葉軍．?dāng)?shù)學(xué)奧林匹克教程［M］．長沙:湖南師范大學(xué)出版社，1998．