二項(xiàng)分布若干性質(zhì)的思考

●李 輝 (杭州外國(guó)語(yǔ)學(xué)校 浙江杭州 310023)

二項(xiàng)分布若干性質(zhì)的思考

●李 輝 (杭州外國(guó)語(yǔ)學(xué)校 浙江杭州 310023)

我們知道:若離散型隨機(jī)變量ζ的分布列為P(ζ =k)=Cknpk(1 －p)n－k，k=0，1，2，…，n，其中0≤p≤1，則稱 ζ服從二項(xiàng)分布，記作 ζ～B(n，p)．二項(xiàng)分布的使用條件為:在n次獨(dú)立重復(fù)試驗(yàn)中，某事件發(fā)生的次數(shù)即服從二項(xiàng)分布．二項(xiàng)分布是概率教學(xué)中一個(gè)非常重要的分布，本文通過(guò)對(duì)二項(xiàng)分布的一些思考，期望有助于讀者對(duì)二項(xiàng)分布的理解．

例1在10件產(chǎn)品中有2件次品，連續(xù)抽3次，每次抽1件．

(1)當(dāng)放回抽樣時(shí)，求抽到的次品數(shù)ζ的分布列;

(2)當(dāng)不放回抽樣時(shí)，求抽到的次品數(shù)η的分布列．

解(1)根據(jù)題意容易求得ζ的分布列如表1所示．

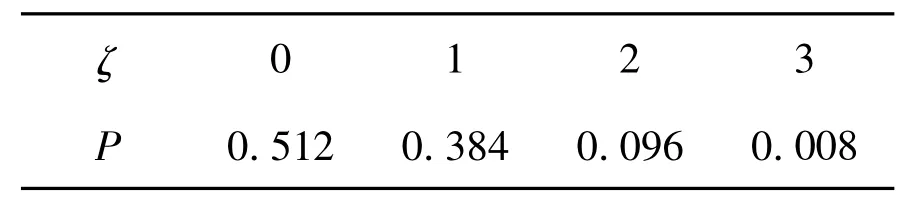
表1 ζ的分布列

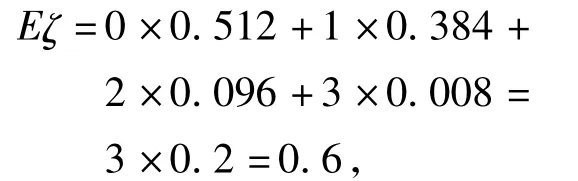
(2)根據(jù)題意可求得η的分布列如表2所示．

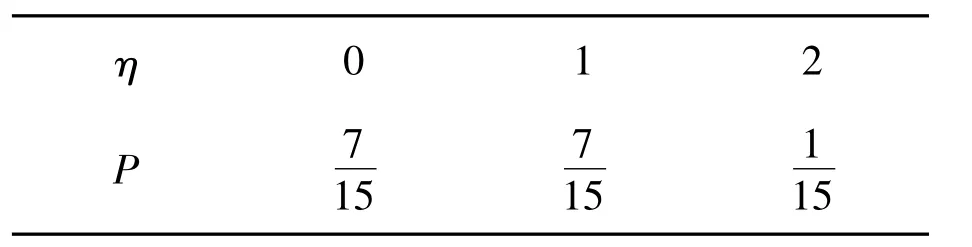
表2 η的分布列

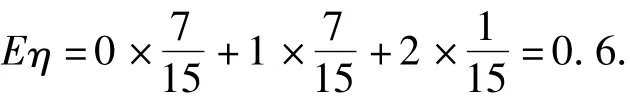
顯然，2種不同的抽樣方式并沒(méi)有改變次品數(shù)的數(shù)學(xué)期望．

思考1放回與不放回為什么不影響數(shù)學(xué)期望?

問(wèn)題一般化:設(shè)在N件產(chǎn)品中有M(M≤N)件不合格品，從中任取n(n≤N)件進(jìn)行檢查，求取得不合格品數(shù)ζ的數(shù)學(xué)期望．

這里，還假定取出的產(chǎn)品數(shù)不超過(guò)合格品總數(shù)，即n≤N－M．若沒(méi)有這個(gè)假定，則隨機(jī)變量ζ的取值范圍應(yīng)是 s，s+1，s+2，…，m，其中 m=min{M，n}，s=max{0，n－(N －M)}．在具體問(wèn)題中不難理解，例如共有10件產(chǎn)品，其中次品數(shù)為6，從中取出5件產(chǎn)品，則取出的產(chǎn)品中次品數(shù)ζ的取值范圍是 1，2，3，4，5．

(1)當(dāng)放回抽樣時(shí)，ζ服從二項(xiàng)分布

通過(guò)上述算式可以看出:放回與不放回確實(shí)不影響次品數(shù)的數(shù)學(xué)期望．我們也可以從另一個(gè)角度來(lái)理解:放回抽樣是n次獨(dú)立重復(fù)試驗(yàn)，每次取到次品的概率都是P=，概率本身就是一種“理想”，因此每次取到“理想”的次品數(shù)都是件，n次獨(dú)立重復(fù)試驗(yàn)取到“理想”的次品數(shù)當(dāng)然是np;不放回抽樣等價(jià)于放回抽樣．把每個(gè)產(chǎn)品看成由的次品和1－的合格品組成，可以認(rèn)為每次取出一件產(chǎn)品，抽到次品的概率仍為，因此n次不放回的抽樣等同于放回抽樣，仍看作n次獨(dú)立重復(fù)試驗(yàn)，即每次抽到次品的概率都是，故不放回的次品數(shù)的數(shù)學(xué)期望與放回的次品數(shù)的數(shù)學(xué)期望相等．這是一種對(duì)于放回與不放回不影響數(shù)學(xué)期望的樸素的理解方式．

思考2二項(xiàng)分布與其他分布有什么關(guān)系?

超幾何分布與二項(xiàng)分布的關(guān)系:第一:在n次試驗(yàn)中，取得不合格品數(shù)X可能服從超幾何分布或二項(xiàng)分布．當(dāng)這n次試驗(yàn)是獨(dú)立重復(fù)試驗(yàn)時(shí)，X服從二項(xiàng)分布;當(dāng)這n次試驗(yàn)是不放回抽取時(shí)，X服從超幾何分布．第二:在不放回n次抽取試驗(yàn)中，抽到的次品數(shù)X服從超幾何分布．但是當(dāng)產(chǎn)品的數(shù)目N很大時(shí)，因?yàn)?/p>

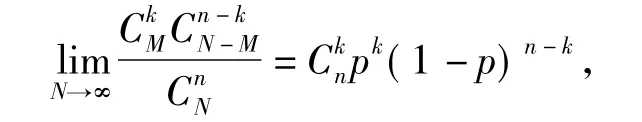
所以X的分布列近似于二項(xiàng)分布，并且隨著X的增加，這種近似的精確度也會(huì)增加．

兩點(diǎn)分布與二項(xiàng)分布的關(guān)系:若隨機(jī)變量X的分布列具有表3所示的形式，則稱X服從兩點(diǎn)分布，p=P(X=1)稱為成功概率．

表3 X的分布列

容易求得

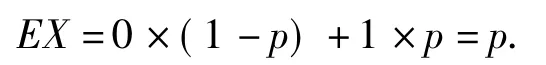
兩點(diǎn)分布是最簡(jiǎn)單的離散型隨機(jī)變量，它是二項(xiàng)分布的基礎(chǔ)，也是二項(xiàng)分布的一個(gè)特例，即n=1時(shí)的二項(xiàng)分布．二項(xiàng)分布可以看作是兩點(diǎn)分布的一般形式，因?yàn)閚次獨(dú)立重復(fù)試驗(yàn)每次的數(shù)學(xué)期望都是p，所以從整體上看n個(gè)獨(dú)立的兩點(diǎn)分布即為二項(xiàng)分布，它的期望當(dāng)然是n個(gè)期望的和，即

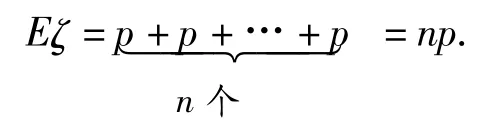
幾何分布與二項(xiàng)分布的關(guān)系:若離散型隨機(jī)變量ζ的分布列為

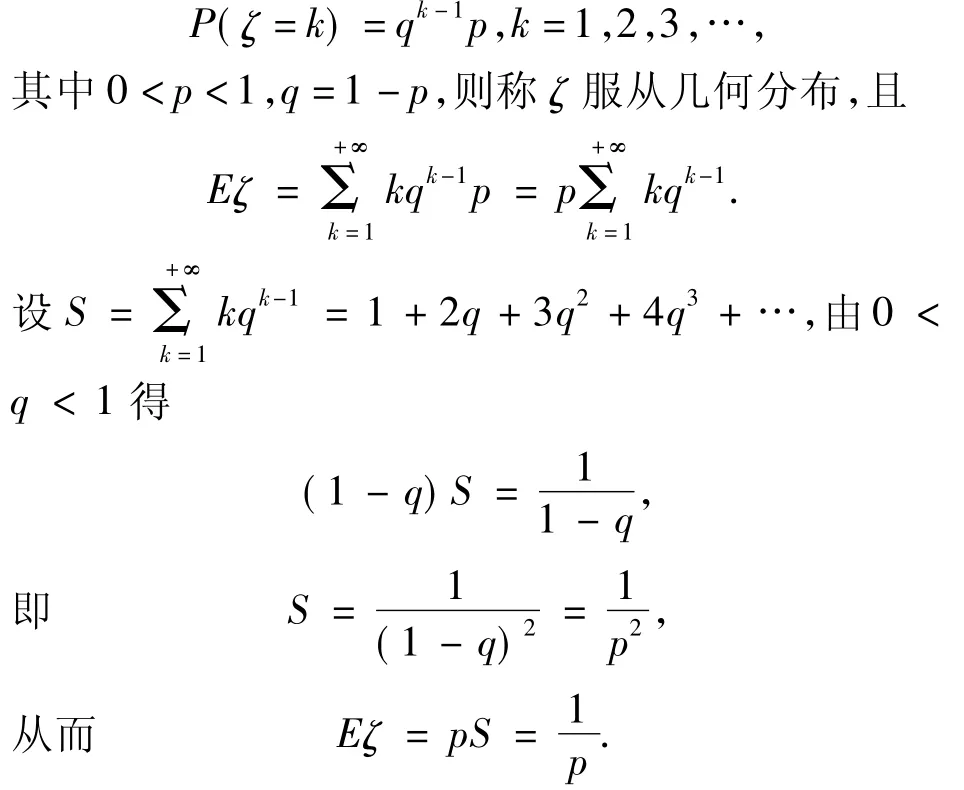
另外在二項(xiàng)分布中，n的值是確定的，ζ的取值是變化的，Eζ是由n和p決定的，但若反過(guò)來(lái)認(rèn)為n的取值是可變的，n=1，2，3，…，則 ζ=1 始終成立，即Eζ=1．又因?yàn)閹缀畏植家彩仟?dú)立重復(fù)試驗(yàn)，即每次試驗(yàn)事件發(fā)生的概率p也是不變的，所以

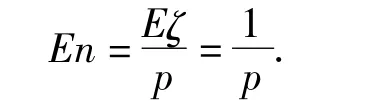
這時(shí)，幾何分布和二項(xiàng)分布只是一個(gè)問(wèn)題的2個(gè)方面罷了，關(guān)鍵是哪個(gè)量作為隨機(jī)變量．

思考3如果二項(xiàng)分布的數(shù)學(xué)期望是np，那么服從二項(xiàng)分布的隨機(jī)變量取何值時(shí)的概率是最大的?

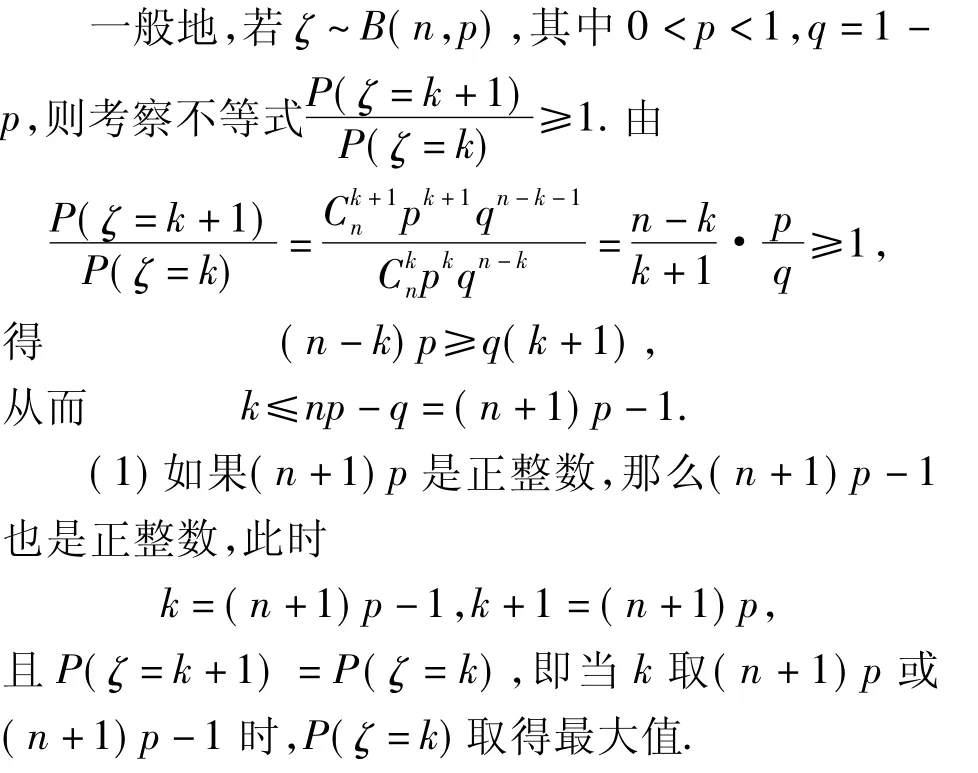
我們可以看出在二項(xiàng)分布的數(shù)學(xué)期望附近的概率達(dá)到最大值，這具有一種必然性．因?yàn)閿?shù)學(xué)期望反映了隨機(jī)變量取值的平均水平，通過(guò)大量的隨機(jī)試驗(yàn)，有大量的隨機(jī)變量的取值相對(duì)聚集在平均水平附近，所以隨機(jī)變量在數(shù)學(xué)期望附近的概率達(dá)到最大值．

數(shù)學(xué)期望本身就是一種“數(shù)學(xué)理想”，概率也是一種“數(shù)學(xué)理想”．對(duì)于“理想”的理解更有助于我們對(duì)于概率概念的理解．概率是發(fā)生于大量的隨機(jī)試驗(yàn)中的，只要這個(gè)試驗(yàn)的次數(shù)足夠地多，頻率就逐漸地趨向于概率．概率是一個(gè)理論值．只要這個(gè)試驗(yàn)的次數(shù)足夠地多，試驗(yàn)出來(lái)的隨機(jī)變量的平均值就會(huì)趨向于這個(gè)隨機(jī)變量的理論的平均值，即它的數(shù)學(xué)期望．它是一個(gè)平衡點(diǎn)，具有一種必然性，是發(fā)生于大量偶然中的必然．