函數(shù)與方程的思想在高考解題中的運用

●蔣際明 (湖州中學 浙江湖州 313000)

函數(shù)與方程的思想在高考解題中的運用

●蔣際明 (湖州中學 浙江湖州 313000)

1 高考展望

1．1 考點回顧

函數(shù)與方程是中學數(shù)學中的重要概念，它們之間有著密切的聯(lián)系．函數(shù)與方程的思想方法幾乎滲透到中學數(shù)學的各個領(lǐng)域，在解題中有著廣泛的應(yīng)用．其基本思想方法是依據(jù)題意構(gòu)造恰當?shù)暮瘮?shù)或建立相應(yīng)的方程來解決問題．

在中學數(shù)學中，很多函數(shù)的問題需要用方程的知識和方法來支持，同時很多方程的問題需要用函數(shù)的知識和方法去解決．譬如對于函數(shù)y=f(x)零點的問題可轉(zhuǎn)化為方程f(x)=0的問題，也可以把函數(shù)y=f(x)看作二元方程y－f(x)=0，從而使函數(shù)與方程相互轉(zhuǎn)化．

1．2 高考預(yù)測

縱觀近幾年的高考試題，對函數(shù)知識的綜合應(yīng)用以及函數(shù)與方程思想等數(shù)學思想方法的考查一直是高考的重點和熱點．在數(shù)學高考試卷中，與函數(shù)相關(guān)的試題所占比例始終在20%左右，且試題中既有靈活多變的客觀性試題，又有能力要求較高的主觀性試題．

在近幾年的高考中，函數(shù)思想的應(yīng)用主要體現(xiàn)在判斷零點存在性、求變量的取值范圍和研究不等式問題等方面;方程思想的應(yīng)用主要體現(xiàn)為4個漸進層次:解方程、含參數(shù)方程討論、將有關(guān)問題轉(zhuǎn)化為對方程的研究和構(gòu)造方程求解等．

筆者預(yù)測2011年高考對函數(shù)與方程思想的考查趨勢:3個“二次”(二次函數(shù)、二次方程、二次不等式)的問題、基本初等函數(shù)性質(zhì)的應(yīng)用、函數(shù)的零點以及函數(shù)圖像交點問題仍將會重點考查，高觀點下的函數(shù)創(chuàng)新試題將會在中高檔題或壓軸題中出現(xiàn)，一般難度也較大．

2 典例剖析

2．1 運用函數(shù)與方程的思想研究函數(shù)零點問題

例1設(shè)函數(shù)f(x)=4sin(2x+1)－x，則在下列區(qū)間中函數(shù)f(x)不存在零點的是 ( )

A．［－4，－2］ B．［－2，0］

C．［0，2］ D．［2，4］

(2010年浙江省數(shù)學高考試題)

分析本題考查函數(shù)零點的概念，函數(shù)的零點、方程的根以及函數(shù)圖像的交點之間的轉(zhuǎn)化思想．函數(shù)f(x)的零點即為函數(shù)g(x)=4sin(2x+1)與h(x)=x圖像的交點．在同一坐標系中作出2個函數(shù)的圖像，易得出 g(x)=4sin(2x+1)在［－4，－2］內(nèi)都大于0，h(x)=x在［－4，－2］內(nèi)小于0，沒有交點，于是函數(shù)f(x)在［－4，－2］內(nèi)不存在零點．故選A．

2．2 運用函數(shù)與方程的思想求參數(shù)的取值范圍

點評本題主要考查了函數(shù)、不等式以及由不等式恒成立求參數(shù)范圍問題，體現(xiàn)了函數(shù)與方程思想的應(yīng)用，是較為典型的恒成立問題．恒成立問題通常可以利用分離變量轉(zhuǎn)化為最值的方法求解．

2．3 運用函數(shù)與方程的思想解決不等式問題

點評看到這個題目自然會想到直接將條件進行變形，這樣就會變得相當復(fù)雜．而運用方程的思想構(gòu)造二次方程并利用根的判別式，使問題很快得到解決．例4設(shè)二次函數(shù)f(x)=ax2+bx+c(a＞0)，方程f(x)－x=0的2個根x1，x2滿足0＜x1＜x2＜．當 x∈(0，x)時，證明:x＜f(x) ＜x．

11

分析在已知方程f(x)－x=0兩根的情況下，根據(jù)函數(shù)與方程根的關(guān)系，可以寫出函數(shù)f(x)－x的表達式，從而得到函數(shù)f(x)的表達式．

證明由題意可知

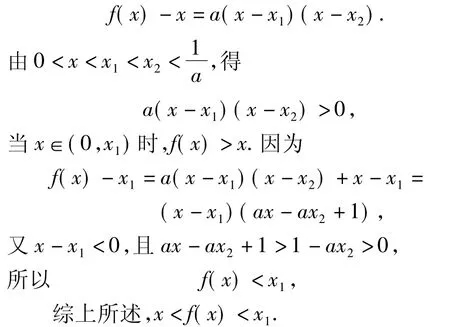
點評本題以二次函數(shù)為本源，選擇了二次函數(shù)的兩根式y(tǒng)=a(x－x1)(x－x2)，從而直接顯示出二次函數(shù)與方程根的關(guān)系，利用二次函數(shù)的兩根式證明不等式可以起到不必再因式分解就可以判斷出差值正負的功效．

2．4 運用函數(shù)與方程的思想解決數(shù)列問題

例5設(shè)a1，d為實數(shù)，首項為a1，公差為d的等差數(shù)列{an}的前n項和為Sn，滿足S5S6+15=0，則 d 的取值范圍是＿＿ ．

點評本題雖然考查等差數(shù)列的前n項和公式，但解題中運用了一元二次方程有實根的判定方法，體現(xiàn)了函數(shù)與方程的思想．

2．5 運用函數(shù)與方程的思想解決解析幾何題

(2010年浙江省數(shù)學高考試題)

例6已知橢圓C:1=1(a＞b＞0)的右頂點為A(1，0)，過 C1的焦點且垂直長軸的弦長為1．

圖1

(1)求橢圓C1的方程．

(2)設(shè)點P在拋物線C2:y=x2+h(h∈R)上，C2在點P處的切線與C1交于點M，N．當線段AP的中點與MN中點的橫坐標相等時，求h的最小值．

(2009年浙江省數(shù)學高考試題)

點評求參數(shù)的取值范圍是解析幾何中的重要問題．解決這類問題一般有2種途徑:其一是建立目標函數(shù)，利用目標函數(shù)的定義域、值域、單調(diào)性等知識來解決;其二是構(gòu)建一元二次方程，利用方程的思想，特別是運用根的判別式、韋達定理等知識，從而使問題巧妙解決．

精題集粹