力的第四要素

張憲恩，陳朝軍，宣志剛

(1.攀枝花攀鋼集團設計研究院有限公司，四川攀枝花617023;2.新鋼釩技改部，四川攀枝花617000)

力的三要素概念(大小、方向、作用點)已深入人心，解決了自然界中大部分力學問題。力的三要素作用的對象是一個單體、一個單質(zhì)點。本文分析、論述力的第四要素。

1 研究對象

讓我們假設，有a球、b球兩個球用桿c連接(見圖1)，a球、b球、桿c組成了一個系統(tǒng)(以下簡稱系統(tǒng))。現(xiàn)在，讓我們分析一下在a球受力后，b球的運動規(guī)律。記a球、b球的質(zhì)量分別是ma、mb，桿c無質(zhì)量，只有剛度。桿的剛度有兩種，其一，桿的抗側(cè)移剛度，抗側(cè)移剛度記為kc1;其二，桿的縱向剛度，其縱向剛度記為kc2。

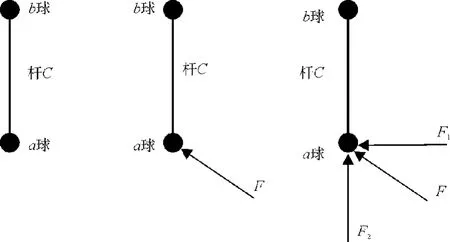
圖1 球的受力

首先，a球受力多種多樣。無論a球受怎樣一個力，它都可以簡化為兩個力:一個力(記為F1)是作用于a球、垂直于桿的軸線;一個力(記為F2)是作用于a球，平行于桿的軸線(見圖1(c))。F2作用時，系統(tǒng)只作平動。F1作用時，若無別的什么力，系統(tǒng)開始受力時作以b球為圓心、桿的長度為半徑的圓周運動，隨后，由于a球作圓周運動，就要產(chǎn)生離心力，那么系統(tǒng)作沿著離心力與F1合力的方向的運動。這個運動不是本文研究的對象。本文研究的對象是，在F1作用下，在a球上施加一個使系統(tǒng)沿F1方向運動的彎矩，使系統(tǒng)沿F1方向運動的規(guī)律。F2已使系統(tǒng)沿F2方向運動，其運動規(guī)律與F1之相同，所不同的是，桿的縱向剛度遠大于桿的抗側(cè)移剛度。下面僅論述F1作用下，系統(tǒng)沿F1方向的運動規(guī)律。

2 運動形態(tài)分析

現(xiàn)在讓我們分析系統(tǒng)在F1作用下沿F1方向的運動。當a球作用F1時，a球就運動，那么b球?qū)⒃趺礃幽亍＿@時，b球有三種狀態(tài):b球先于a球運動而運動;b球與a球同時運動;b球后滯于a球運動而運動。對第一種狀態(tài)是絕對不會發(fā)生的，因b球未先于a球受力。對于第二狀態(tài)，當F1緩慢由小向大增加時就發(fā)生了，a球、b球、桿c同時運動。這時，a球、b球、桿c組成了一個剛體，它們之間無運動差異。對第三種狀態(tài)，當F1很快地由小向大增加時就發(fā)生了。讓我們想象一下系統(tǒng)的運動，a球受力后很快位移，b球靜止，桿c產(chǎn)生彎曲。b球后滯于a球運動。我們稱力F1由小(大)向大(小)的增加(或減少)、或力的方向改變、或二者都有，為力F1的變化速度。

那么，力的變化速度多大時，系統(tǒng)組成的系統(tǒng)不是剛體。讓我們分析a球在F1作用下運動、b球的運動原理。a球在F1作用下運動，由于桿的抗側(cè)移剛度，使得a球在桿中產(chǎn)生剪力，桿又將這個剪力傳至b球，使b球受力，b球受力后就運動。但是在F1作用下a球運動，由桿的抗側(cè)移剛度、b球的質(zhì)量，使得b球運動后滯于a球。

3 質(zhì)點反應的概念

這里引入一個概念—質(zhì)點反應。質(zhì)點反應的定義是:在a球上作用一個變化速度較大的力，使得b球運動后滯于a球的運動，這時，b球后滯于a球運動的時間稱為質(zhì)點反應。

質(zhì)點反應的大小與桿的抗側(cè)移剛度、b球的質(zhì)量有關(guān)。桿的抗側(cè)移剛度越大，質(zhì)點反應就越小。b球的質(zhì)量越大，質(zhì)點反應就越大。讓我們觀察一下彈性單擺的運動規(guī)律，一個單質(zhì)點與支座之間用一個彈簧片連接，我們給質(zhì)點一個初始位移使之自由振動。質(zhì)點由平衡位置至一側(cè)最大位移，再經(jīng)過平衡位置至另一側(cè)最大位移，最后到平衡位置所需要的時間稱為周期。那么，質(zhì)點由平衡位置至最大位移所需要的時間是四分之一周期，這個四分之一周期是否是b球的后滯于a球運動的時間呢。換句話講，質(zhì)點的四分之一周期是否為質(zhì)點反應呢，這個需要實驗驗證。現(xiàn)在，我們只有假定，質(zhì)點反應的值為質(zhì)點自由振動的四分之一周期。

式中:f為質(zhì)點反應;m為質(zhì)點質(zhì)量;k為桿抗側(cè)移剛度。

4 質(zhì)點反應的作用

有了質(zhì)點反應的概念后，系統(tǒng)組成一個系統(tǒng)，在a球受力狀態(tài)下為非剛體的條件是，力的變化速度在a球中產(chǎn)生位移所需要的時間與b球的質(zhì)點反應相近。也就是說力的變化速度產(chǎn)生的效應接近b球的質(zhì)點反應時，系統(tǒng)組成的系統(tǒng)為非剛體。力的變化速度產(chǎn)生的效應遠離b球的質(zhì)點反應時，系統(tǒng)組成的系統(tǒng)為剛體。

從上面分析可以看出，力的變化速度決定著一個系統(tǒng)是否為剛體，因此，力的第四要素是力的變化速度。

5 運動形態(tài)分析推廣

前面的分析是建立在系統(tǒng)靜止狀態(tài)，經(jīng)過分析，系統(tǒng)處于任何狀態(tài)均可。無論系統(tǒng)處于什么狀態(tài)，只要a球受變化的力，其速度發(fā)生變化，只要這個變化的力的效應接近b球的質(zhì)點反應、且質(zhì)點反應起作用，那么，b球的速度變化就后滯于a球的速度變化。

6 作用

力的第四要素有什么作用呢。力的三要素作用的對象是單體、單質(zhì)點，因此，力的三要素研究的是單體、單質(zhì)點靜止或運動狀態(tài)的力學關(guān)系及運動規(guī)律。力的三要素加上力的第四要素作用的對象是相關(guān)的雙體。因此，力的四要素研究是相關(guān)雙體的在質(zhì)點反應起作用時的運動規(guī)律。若力的第四要素特別小，以致使質(zhì)點反應不起作用，這時，系統(tǒng)為剛體，此時，其運動(狀態(tài))規(guī)律與力的三要素的規(guī)律無差異。

既然力的四要素是研究相關(guān)雙體的運動規(guī)律，因此，凡是能簡化為相關(guān)雙體運動的問題，可用力的四要素去解決，如碰撞，爆炸，建筑物的地震反應。

7 結(jié)束語

由于作者沒有實驗的條件，本文未經(jīng)實驗證實，歡迎有實驗條件的同行采用各種途徑用實驗驗證力的第四要素。

［1］浙江大學理論力學教研室編.理論力學(第四版)［M］.北京:高等教育出版社，2009

［2］李卓球，朱四榮.工程力學［M］.武漢理工大學出版社，2008