基于虛擬脈沖響應(yīng)函數(shù)與神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)損傷定位研究

張啟亮，刁延松，佟顯能，于 菲

(1.青島理工大學(xué)土木工程學(xué)院，山東青島266033;2.青島同圓建筑設(shè)計(jì)有限公司，山東青島266000)

基于振動(dòng)測(cè)試的結(jié)構(gòu)損傷定位方法一般是由結(jié)構(gòu)的振動(dòng)響應(yīng)來(lái)提取結(jié)構(gòu)的損傷特征參數(shù)，再根據(jù)結(jié)構(gòu)的損傷特征參數(shù)來(lái)判斷結(jié)構(gòu)的損傷狀況，故結(jié)構(gòu)的損傷特征參數(shù)的選取直接關(guān)系到損傷定位結(jié)果的優(yōu)劣。常用的結(jié)構(gòu)特征參數(shù)有固有頻率、模態(tài)振型及模態(tài)阻尼等模態(tài)參數(shù)。近年來(lái)，模態(tài)參數(shù)因其直接反映結(jié)構(gòu)的狀況而備受關(guān)注。但是模態(tài)參數(shù)受環(huán)境(如溫度、濕度等)、工況及結(jié)構(gòu)本身不確定性的影響很大，故基于模態(tài)參數(shù)的方法應(yīng)用在工程實(shí)際中的很少。目前，已有學(xué)者陸續(xù)提出了一些非模態(tài)特征參數(shù)，如Biswajit［1］利用小波系數(shù)研究了雙線性結(jié)構(gòu)與遲滯系統(tǒng)的剛度衰減及損傷定位問(wèn)題;Law［2］等通過(guò)小波包方法計(jì)算了結(jié)構(gòu)的小波包能量及其分布以此檢測(cè)定位損傷;Nichols［3］等人比較了吸引子維數(shù)和關(guān)聯(lián)維數(shù)識(shí)別損傷的結(jié)果，得出前者比后者更準(zhǔn)確的結(jié)論;Rutolo［4］等人將不同工況下的頻率響應(yīng)組成Hankle矩陣，奇異值分解法計(jì)算矩陣的秩后，根據(jù)秩的不同判斷結(jié)構(gòu)是否發(fā)生變化等等。這些方法都是以人工激勵(lì)作為輸入的。然而像跨海大橋、海洋平臺(tái)等大型土木工程結(jié)構(gòu)其結(jié)構(gòu)復(fù)雜、體積龐大、造價(jià)昂貴，所處的環(huán)境惡劣，人工激勵(lì)難以施加并且費(fèi)用較高，環(huán)境荷載激勵(lì)難以測(cè)試。針對(duì)這種情況，本文直接利用白噪聲激勵(lì)下結(jié)構(gòu)兩點(diǎn)響應(yīng)構(gòu)造虛擬脈沖響應(yīng)函數(shù)，并對(duì)虛擬脈沖響應(yīng)函數(shù)的幅值進(jìn)行了小波包分解并計(jì)算其節(jié)點(diǎn)能量，以結(jié)構(gòu)損傷前后的小波包節(jié)點(diǎn)能量變化量作為損傷特征向量，利用BP神經(jīng)網(wǎng)絡(luò)的模式分類功能進(jìn)行結(jié)構(gòu)損傷定位研究。海洋平臺(tái)結(jié)構(gòu)單損傷和多損傷的數(shù)值模擬結(jié)果表明，當(dāng)結(jié)構(gòu)損傷程度較大時(shí)，該方法是可行的并且具有較強(qiáng)的噪聲魯棒性。

1 基本理論

1.1 虛擬脈沖響應(yīng)函數(shù)的獲取［5］

現(xiàn)實(shí)中的大型土木工程結(jié)構(gòu)如跨海大橋和海洋平臺(tái)等所受的環(huán)境激勵(lì)往往難以測(cè)得，而對(duì)結(jié)構(gòu)動(dòng)力系統(tǒng)，其激勵(lì)與響應(yīng)之間的關(guān)系是通過(guò)系統(tǒng)本身所固有的動(dòng)力特性——脈沖響應(yīng)函數(shù)或頻率響應(yīng)函數(shù)來(lái)體現(xiàn)的。脈沖響應(yīng)函數(shù)中包含了系統(tǒng)所有的動(dòng)力特性參數(shù)。因此本文直接利用白噪聲激勵(lì)下結(jié)構(gòu)兩點(diǎn)響應(yīng)構(gòu)造虛擬脈沖響應(yīng)函數(shù)。虛擬脈沖響應(yīng)函數(shù)的基本思想是以參考點(diǎn)的動(dòng)力響應(yīng)作為虛擬激勵(lì)，計(jì)算參考點(diǎn)的虛擬激勵(lì)與其他測(cè)點(diǎn)響應(yīng)之間的虛擬脈沖響應(yīng)函數(shù)，用來(lái)表征結(jié)構(gòu)動(dòng)力系統(tǒng)的動(dòng)力響應(yīng)。其理論分析見(jiàn)文獻(xiàn)［5］。為了便于敘述給出頻率響應(yīng)函數(shù)的公式:

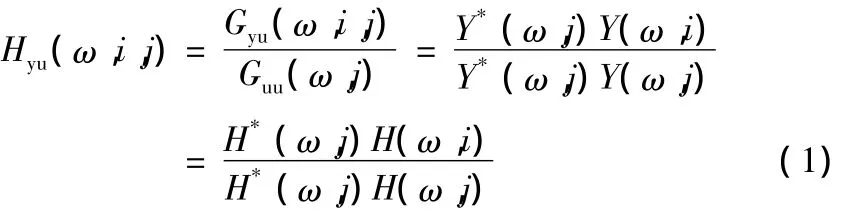
式中:Gyu(w，i，j)和 Guu(w，j)分別為參考點(diǎn) j的響應(yīng)(虛擬激勵(lì))xj(t)和測(cè)點(diǎn)i的響應(yīng)xi(t)的互譜密度以及虛擬激勵(lì)xj(t)的自譜密度;Y(w)為響應(yīng)的傅里葉變換;Y(w，i)和Y(w，j)分別是響應(yīng)xi(t)和虛擬激勵(lì)xj(t)的傅里葉變換;Y*(w，j)是 Y(w，j)的復(fù)共軛;Hyu(w，i，j)、H(w)均為頻率響應(yīng)函數(shù);H*(w，j)為H(w，j)的復(fù)共軛。

從公式中可以看出，兩點(diǎn)響應(yīng)的頻率響應(yīng)函數(shù)Hyu(w，i，j)能有效地消除激勵(lì)頻譜的影響，也就是說(shuō)，對(duì)頻率響應(yīng)函數(shù)Hyu(w，i，j)進(jìn)行逆傅里葉變換求得的虛擬脈沖響應(yīng)函數(shù)可以有效地克服激勵(lì)的隨機(jī)性和不確定性，具有更好的激勵(lì)魯棒性，更好地反映了結(jié)構(gòu)動(dòng)力系統(tǒng)的動(dòng)力特性。故可以將虛擬脈沖響應(yīng)函數(shù)應(yīng)用于結(jié)構(gòu)的損傷定位。

1.2 虛擬脈沖響應(yīng)函數(shù)的小波包分解

當(dāng)結(jié)構(gòu)系統(tǒng)的激勵(lì)力向量一定時(shí)(假設(shè)忽略觀測(cè)噪聲)，結(jié)構(gòu)損傷所引起的結(jié)構(gòu)動(dòng)力特性的變化，必定會(huì)引起不同小波包尺度(頻帶)上結(jié)構(gòu)響應(yīng)f(i，k)的變化，從而引起結(jié)構(gòu)動(dòng)力響應(yīng)f(N，k)的能量在各個(gè)頻帶內(nèi)的重新分布［5］。因此，結(jié)構(gòu)動(dòng)力響應(yīng)f(N，k)在第i分解層的小波包能量譜向量Ei可以表示結(jié)構(gòu)的損傷狀態(tài):

式中:fi，j表示第 i層分解節(jié)點(diǎn)(i，j)上的結(jié)構(gòu)響應(yīng)。

文獻(xiàn)［6］論述了結(jié)構(gòu)損傷前后小波包節(jié)點(diǎn)能量變化量比小波包節(jié)點(diǎn)能量對(duì)損傷位置更為敏感，本文以此為依據(jù)假設(shè)對(duì)白噪聲激勵(lì)下所得的虛擬脈沖響應(yīng)函數(shù)f的幅值進(jìn)行i層小波包分解，則虛擬脈沖響應(yīng)函數(shù)f的幅值在第i分解層的小波包節(jié)點(diǎn)能量向量Ei可以表征結(jié)構(gòu)的動(dòng)力特性。

采用Db25小波作為結(jié)構(gòu)損傷定位的小波函數(shù)，選用適宜的小波函數(shù)階次和小波包分解層次對(duì)虛擬脈沖響應(yīng)函數(shù)幅值進(jìn)行小波包分解。將結(jié)構(gòu)損傷前后小波包節(jié)點(diǎn)能量變化量作為結(jié)構(gòu)損傷定位因子，對(duì)結(jié)構(gòu)進(jìn)行損傷定位。

小波包節(jié)點(diǎn)能量變化量為:

歸一化的小波包節(jié)點(diǎn)能量變化量為:

1.3 BP神經(jīng)網(wǎng)絡(luò)

BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)簡(jiǎn)單，算法容易實(shí)現(xiàn)，它最早被應(yīng)用于結(jié)構(gòu)的損傷識(shí)別中，也是目前應(yīng)用最為廣泛的人工神經(jīng)網(wǎng)絡(luò)模型。本文采用三層BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，即一個(gè)輸入層、一個(gè)隱含層和一個(gè)輸出層。理論證明三層的BP網(wǎng)絡(luò)可以表示任意一個(gè)映射關(guān)系［7］。

BP神經(jīng)網(wǎng)絡(luò)的輸入向量直接關(guān)系到網(wǎng)絡(luò)識(shí)別效果，現(xiàn)采用如下方式構(gòu)造輸入向量。

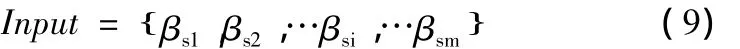
其中βsi(i=1，2，…，m)為歸一化的結(jié)構(gòu)損傷前后虛擬脈沖響應(yīng)函數(shù)幅值第s層小波包分解第i個(gè)頻帶節(jié)點(diǎn)能量變化量。本文所用的神經(jīng)網(wǎng)絡(luò)的輸出向量為:

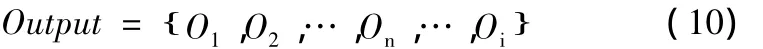
其中Oi∈［0，1］。對(duì)于識(shí)別損傷位置的神經(jīng)網(wǎng)絡(luò)，Oi≈0.0表示i處沒(méi)有損傷，而Oi≈1.0表示在i處有損傷。

1.4 基本步驟

第一步，獲取虛擬脈沖響應(yīng)函數(shù)。利用ANSYS10.0對(duì)海洋平臺(tái)三維有限元模型進(jìn)行時(shí)程反應(yīng)分析獲得節(jié)點(diǎn)加速度，然后利用MATLAB6.5編程獲得虛擬脈沖響應(yīng)函數(shù)。

第二步，獲取損傷特征向量。利用MATLAB6.5對(duì)第一步獲得的虛擬脈沖響應(yīng)函數(shù)進(jìn)行小波包分解獲得節(jié)點(diǎn)能量，然后提取結(jié)構(gòu)損傷前后節(jié)點(diǎn)能量變化量作為損傷定位特征向量。

第三步，將損傷定位特征向量作為BP神經(jīng)網(wǎng)絡(luò)的輸入進(jìn)行網(wǎng)絡(luò)訓(xùn)練，最后將測(cè)試樣本輸入訓(xùn)練好的網(wǎng)絡(luò)進(jìn)行損傷定位。

2 數(shù)值模擬

2.1 有限元模型

本文利用ANSYS10.0建立如圖1所示的海洋平臺(tái)結(jié)構(gòu)的三維有限元模型。基本參數(shù)如下:彈性模量為E=2.07×1011N/m2，密度為7 800 kg/m3，柱、橫梁和支撐采用 BEAM4單元，頂板采用SHELL63單元，頂板上堆積質(zhì)量采用MASS21單元進(jìn)行模擬。該模型共有32個(gè)結(jié)點(diǎn)，50個(gè)BEAM4單元，1個(gè)SHELL63單元，4個(gè)MASS21單元。利用ANSYS10.0的時(shí)程反應(yīng)分析模塊進(jìn)行時(shí)程反應(yīng)分析，獲得完好結(jié)構(gòu)和損傷結(jié)構(gòu)時(shí)的加速度響應(yīng)信號(hào)，激勵(lì)采用白噪聲，沿Y向作用于二層結(jié)點(diǎn)9和10，采樣頻率是50 Hz，輸出加速度響應(yīng)信號(hào)的采樣頻率是50 Hz，選取四層結(jié)點(diǎn)2和二層結(jié)點(diǎn)10的Y向50 s內(nèi)的加速度響應(yīng)作為研究信號(hào)。

各種損傷工況均采用單元彈性模量折減來(lái)實(shí)現(xiàn)，單元編號(hào)如圖1所示，模擬的損傷工況如表1所示。

表1 損傷工況

圖1 數(shù)值分析模型

2.2 BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練與測(cè)試

以節(jié)點(diǎn)10的加速度響應(yīng)作為虛擬激勵(lì)，計(jì)算完好結(jié)構(gòu)和損傷結(jié)構(gòu)的節(jié)點(diǎn)2的頻率響應(yīng)函數(shù)，在此基礎(chǔ)上采用逆傅里葉變換得到節(jié)點(diǎn)2的虛擬脈沖響應(yīng)函數(shù)。對(duì)虛擬脈沖響應(yīng)函數(shù)的幅值進(jìn)行小波包分解，小波包分解時(shí)采用Db25小波函數(shù)，分解層次取為5。求得完好結(jié)構(gòu)和損傷結(jié)構(gòu)的節(jié)點(diǎn)能量值，進(jìn)而求得結(jié)構(gòu)損傷前后節(jié)點(diǎn)能量變化量。分別對(duì)單損傷和多損傷(這里單指兩處損傷)的損傷工況進(jìn)行了研究，采用結(jié)構(gòu)損傷50%前后節(jié)點(diǎn)能量變化量作為網(wǎng)絡(luò)訓(xùn)練樣本。訓(xùn)練函數(shù)采用TRANLM，學(xué)習(xí)函數(shù)采LEARNGDM。網(wǎng)絡(luò)訓(xùn)練樣本和測(cè)試樣本如表2和表3所示。

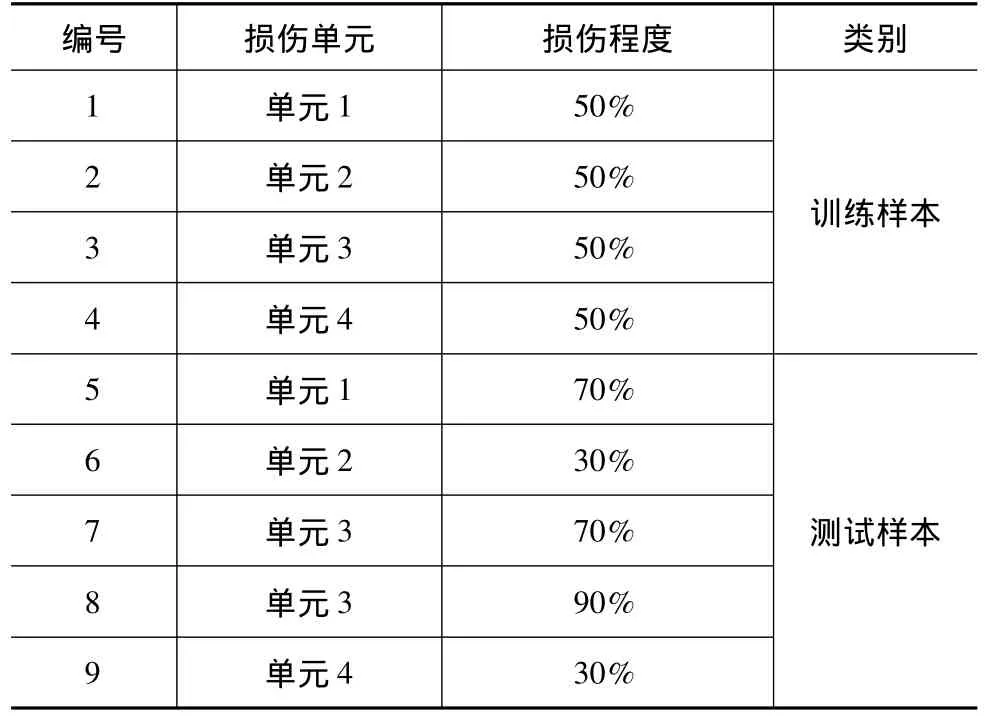
表2 單損傷的訓(xùn)練和測(cè)試樣本

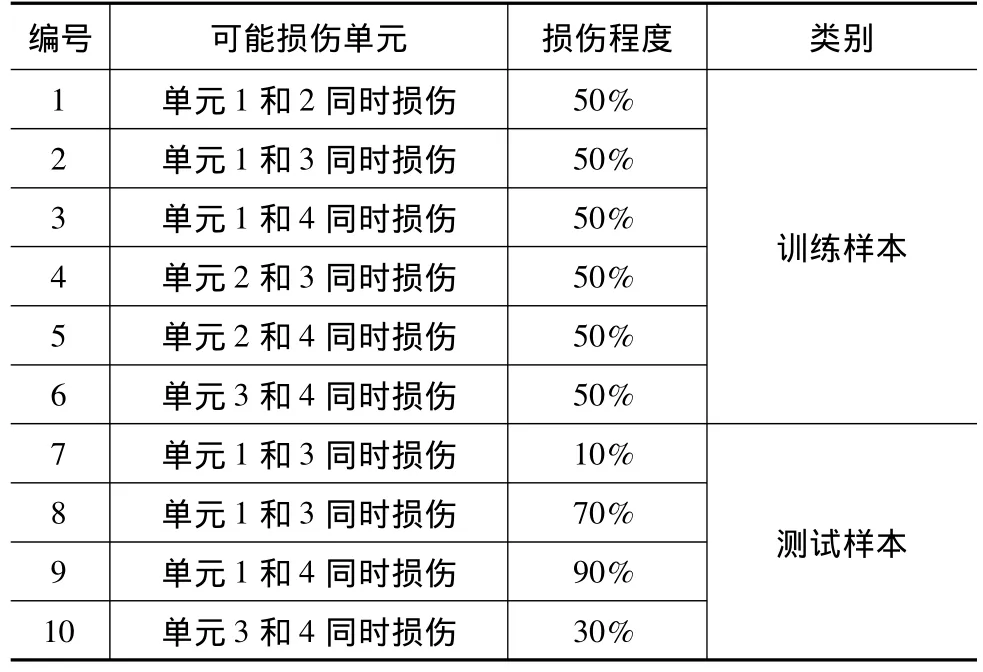
表3 多損傷的訓(xùn)練和測(cè)試樣本

單損傷的網(wǎng)絡(luò)結(jié)構(gòu)為:32×10×4;訓(xùn)練參數(shù)為:最大訓(xùn)練次數(shù)500;訓(xùn)練精度1e－5;學(xué)習(xí)率0.05;顯示訓(xùn)練迭代過(guò)程25;動(dòng)量因子0.9。多損傷的網(wǎng)絡(luò)結(jié)構(gòu)為:32×13×4，訓(xùn)練參數(shù)為:最大訓(xùn)練次數(shù)1000;訓(xùn)練精度1e－5;學(xué)習(xí)率0.1;顯示訓(xùn)練迭代過(guò)程50動(dòng)量因子0.9。單損傷和多損傷的訓(xùn)練過(guò)程和測(cè)試結(jié)果如表4所示。

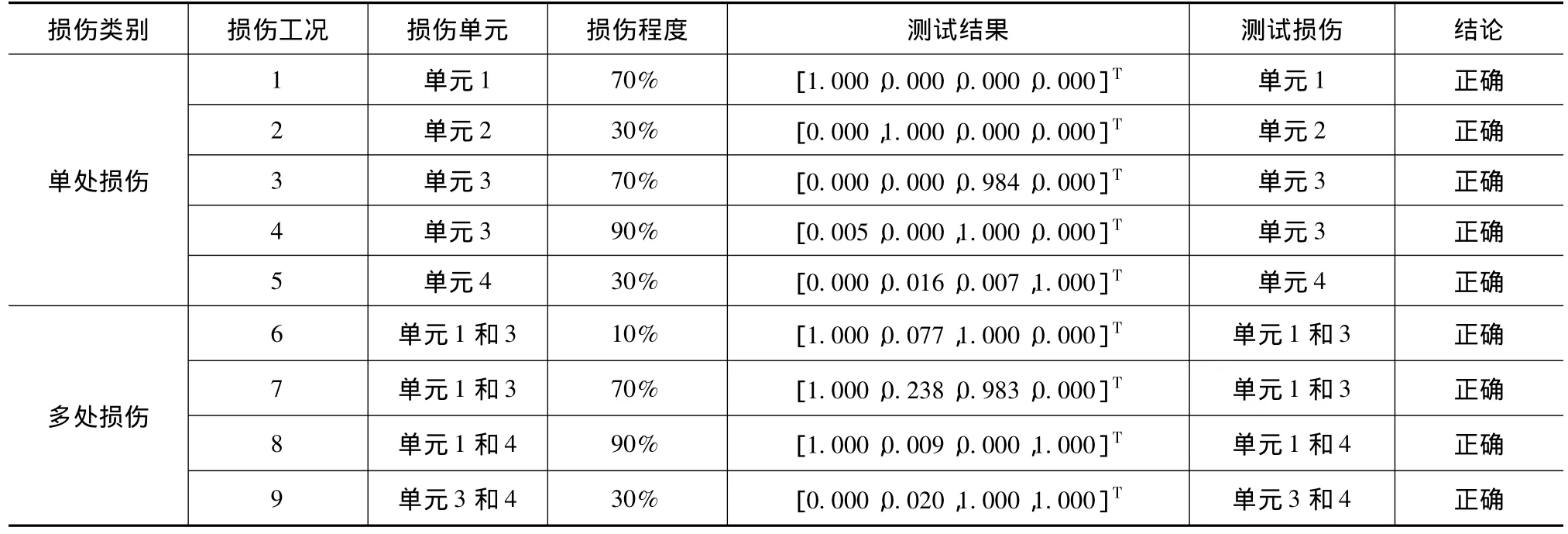
表4 單損傷和多損傷的網(wǎng)絡(luò)訓(xùn)練過(guò)程和測(cè)試結(jié)果

從單損傷和多損傷的網(wǎng)絡(luò)測(cè)試結(jié)果可以看出，該方法能準(zhǔn)確地對(duì)發(fā)生不同程度的損傷結(jié)構(gòu)進(jìn)行損傷定位。

2.3 噪聲魯棒性分析

為考慮測(cè)量噪聲的影響，在加速度信號(hào)中疊加了不同程度的正態(tài)分布的隨機(jī)白噪聲，噪聲的模擬公式為:

式中:γi和分別為無(wú)噪聲和有噪聲時(shí)的加速度信號(hào);εi為正態(tài)分布的隨機(jī)數(shù)(均值為零，均方值為1);p是在測(cè)試樣本上所加噪聲的大小，本文取1%和3%。

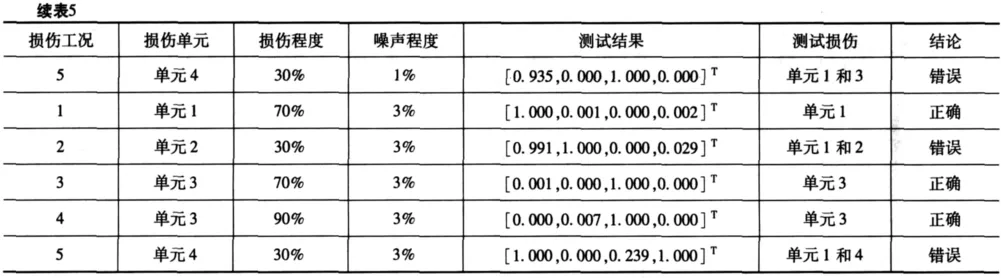
單處損傷時(shí)，加入1%噪聲后的網(wǎng)絡(luò)結(jié)構(gòu)為:32×12×4，訓(xùn)練參數(shù):最大訓(xùn)練次數(shù)100;訓(xùn)練精度1e－5;學(xué)習(xí)率0.1;顯示訓(xùn)練迭代過(guò)程25;動(dòng)量因子0.9。加入3%噪聲后的網(wǎng)絡(luò)結(jié)構(gòu)為:32×11×4，訓(xùn)練參數(shù):最大訓(xùn)練次數(shù)100;訓(xùn)練精度1e－5;學(xué)習(xí)率0.04;顯示訓(xùn)練迭代過(guò)程25;動(dòng)量因子0.9。訓(xùn)練過(guò)程和測(cè)試結(jié)果如表5所示。

?

?

多處損傷時(shí)，加入1%噪聲后的網(wǎng)絡(luò)結(jié)構(gòu)為:32×13×4，訓(xùn)練參數(shù):最大訓(xùn)練次數(shù)1000;訓(xùn)練精度1e－5;學(xué)習(xí)率0.005;顯示訓(xùn)練迭代過(guò)程50;動(dòng)量因子0.9。加入3%噪聲后的網(wǎng)絡(luò)結(jié)構(gòu)為:32×11×4，訓(xùn)練參數(shù):最大訓(xùn)練次數(shù)1000;訓(xùn)練精度1e－5;學(xué)習(xí)率0.008;顯示訓(xùn)練迭代過(guò)程50;動(dòng)量因子0.9。訓(xùn)練過(guò)程和測(cè)試結(jié)果如表6所示。

表6 加入白噪聲后多損傷的網(wǎng)絡(luò)訓(xùn)練過(guò)程和測(cè)試結(jié)果

從加入噪聲后的測(cè)試結(jié)果看，該方法對(duì)結(jié)構(gòu)發(fā)生較大程度損傷時(shí)的單處損傷和多處損傷均能準(zhǔn)確地進(jìn)行損傷定位，但是對(duì)結(jié)構(gòu)發(fā)生較小程度損傷時(shí)的損傷定位，不論是單損傷還是多損傷，都出現(xiàn)誤判現(xiàn)象。造成誤判的原因主要是由于較小程度的損傷引起的結(jié)構(gòu)動(dòng)力響應(yīng)相應(yīng)較小，進(jìn)而造成結(jié)構(gòu)損傷前后節(jié)點(diǎn)能量變化量較小，對(duì)損傷定位不敏感。

從未加入噪聲和加入噪聲后的測(cè)試結(jié)果看，該方法對(duì)結(jié)構(gòu)發(fā)生的較大程度損傷能準(zhǔn)確地識(shí)別出單損傷和多損傷的損傷位置，并且具有較強(qiáng)的噪聲魯棒性，結(jié)果令人滿意，但是該方法對(duì)結(jié)構(gòu)發(fā)生較小程度損傷時(shí)的單損傷和多損傷的損傷定位具有一定的局限性。

3 結(jié)論

直接利用白噪聲激勵(lì)下結(jié)構(gòu)兩點(diǎn)響應(yīng)構(gòu)造虛擬脈沖響應(yīng)函數(shù)，并對(duì)虛擬脈沖響應(yīng)函數(shù)的幅值進(jìn)行小波包分解并計(jì)算其節(jié)點(diǎn)能量。以結(jié)構(gòu)損傷前后的小波包節(jié)點(diǎn)能量變化量作為損傷特征向量，利用BP神經(jīng)網(wǎng)絡(luò)的模式分類功能進(jìn)行結(jié)構(gòu)損傷定位。從數(shù)值模擬結(jié)果看，能夠很好地對(duì)海洋平臺(tái)結(jié)構(gòu)發(fā)生較大程度損傷時(shí)的單損傷和多損傷進(jìn)行損傷定位，并且具有較強(qiáng)的噪聲魯棒性，但是對(duì)海洋平臺(tái)結(jié)構(gòu)較小程度的損傷進(jìn)行損傷定位具有一定的局限性。另外，對(duì)海洋平臺(tái)結(jié)構(gòu)其它構(gòu)件損傷位置的識(shí)別和損傷程度的識(shí)別有待進(jìn)一步研究。

［1］Biswajit Basu.Identification of stiffness degradation in structures using wavelet analysis［J］.Construction and Building Materials，2005，19:713 －721

［2］Law S S，Li X Y，Zhu X Q.Structural damage detection from wavelet packet sensitivity［J］.Engineering Structures，2005，27:1339－1348

［3］Nichols J M，Virgin L N.Todd M D.On the use of attracter dimension as a feature in structural health monitoring［J］.Mechanical Systems and Signal Progressing，2003，17(6):1305 －1320

［4］Rutolo R，Surace C.Using SVD to detect damage in structures with different operational conditions［J］.Journal of Sound and Vibration，1999，226(3):425 －439

［5］李愛(ài)群，丁幼亮.工程結(jié)構(gòu)損傷預(yù)警理論及其應(yīng)用［M］.北京:科學(xué)出版社，2007:86－89

［6］刁延松.基于神經(jīng)網(wǎng)絡(luò)和小波分析的海洋平臺(tái)結(jié)構(gòu)損傷檢測(cè)研究［D］.青島:中國(guó)海洋大學(xué)，2006

［7］王柏生，倪一清，高贊明.模型參數(shù)誤差對(duì)用神經(jīng)網(wǎng)絡(luò)進(jìn)行結(jié)構(gòu)損傷識(shí)別的影響［J］.土木工程學(xué)報(bào)，2000，33(1):49 －55