可拓聚類方法在醫院年收治病人數預測中的應用*

濰坊醫學院公共衛生學院(261053) 黎景雪 潘慶忠 房 剛 王培承

可拓聚類方法在醫院年收治病人數預測中的應用*

濰坊醫學院公共衛生學院(261053) 黎景雪 潘慶忠 房 剛 王培承△

目的將可拓聚類方法用于對醫院年收治病人數的預測。方法 構造可拓聚類預測模型，判斷待聚類樣本所屬類別，對其進行預測。結果 利用1981～1989年的相關因素數據資料構造可拓聚類預測模型，對1990年的收治病人數進行預測，結果與實際相符。結論 可拓聚類方法用于對醫院年收治病人數的預測是有效可行的，可以為醫院管理與統計提供一種新的方法。

可拓聚類方法 醫院年收治病人數 關聯函數

*：2009年濰坊醫學院研究生創新基金項目

△通訊作者

可拓學是由我國學者蔡文于1983年創立的一門新學科，它從定性和定量兩個角度去研究解決矛盾問題的規律和方法，為廣大實際工作者，尤其是管理、決策和設計人員提供一種啟發性的思想與分析方法。可拓聚類預測就是根據事物關于特征的量值來判斷其屬于某一類的程度，通過計算關聯函數使聚類定量化。近年來，可拓聚類預測方法已經在工程類學科中廣泛應用，但在醫學領域的應用尚不多見，本文在這方面進行嘗試，為醫學領域提供一種新的預測方法。

醫院年收治病人數是反映醫院工作量的一個重要指標，其大小直接影響醫院的社會效益和經濟效益，它和多種因素有關。本文利用可拓聚類預測方法對醫院年收治病人數做出科學合理的預測，為醫院決策管理提供依據。

原理與方法〔1-4〕

1.原理

可拓學中物元的概念為解決聚類分析問題提供了新的思路，其根據事物關于特征的量值來判斷此事物屬于某一集合的程度。可拓聚類預測方法首先通過聚類分析劃分集合P的若干子集，然后構造經典域物元和節域物元，對于待測物元，通過計算關聯函數值確定其屬于哪個子集，從而得到可拓聚類預測的結果。

2.方法

設Ii(i=1，2，…，m)是P的m個子集，Ii?P(i=1，2，…，m)，對任何待測對象p?P，用以下步驟判斷p屬于哪個子集Ii，并計算p隸屬于任一子集Ii的程度。

(1)確定經典域物元和節域物元

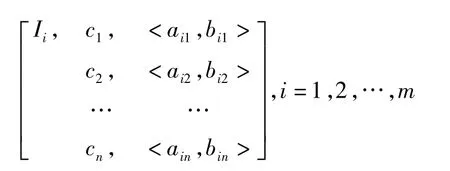
其中，c1，c2，…，cn是Ii的n個不同特征，Xi1，Xi2，…，Xin分別為Ii關于特征c1，c2，…，cn的取值范圍，即經典域。并且有Xij= ＜aij，bij＞(j=1，2，…，n)。

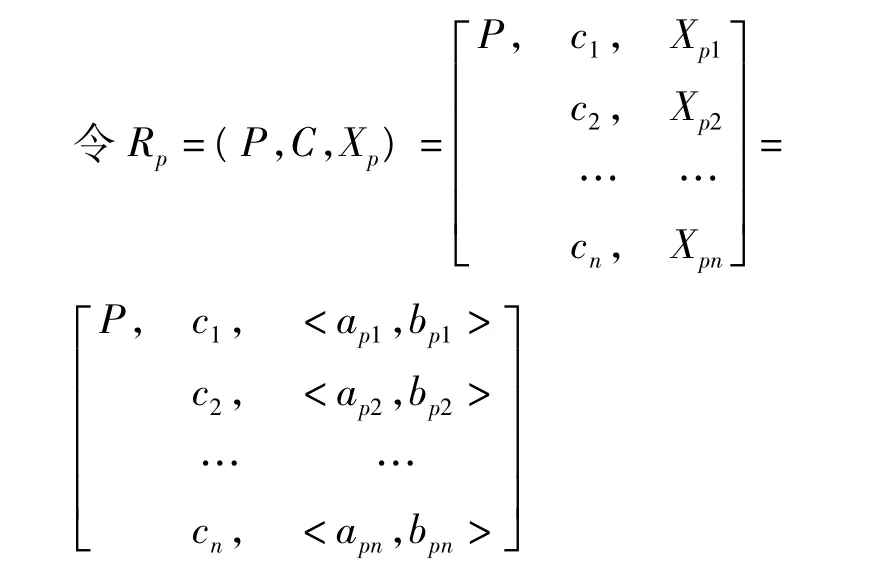
其中，Xp1，Xp2，…，Xpn分別是P關于特征c1，c2，…，cn的取值范圍，即P的節域。并且有Xpj=＜apj，bpj＞(j=1，2，…，n)。

待測樣本形成的物元為

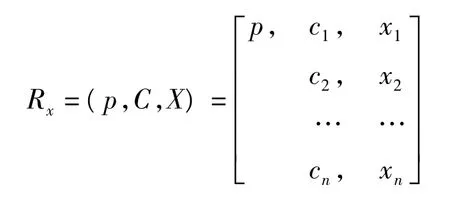
其中，x1，x2，…，xn分別為待測樣本的n個因子的觀測值。

(2)確定關聯函數并計算關聯函數值

待測樣本與各類的關聯度按下列公式計算：

其中x0為K(x)取最大值的點，ρ(xj，Xij)和 ρ(xj，Xpj)稱為點與區間的距，其計算公式為：

(3)確定權系數并計算隸屬程度

權系數的大小對于綜合關聯度的高低具有舉足輕重的作用，為了盡量合理地確定權系數，可以使用層次分析法〔5，6〕來確定各個因子之間的相對重要性次序，從而計算出綜合關聯度。

則待測樣本p對i類的綜合關聯度為：

(4)判定待測樣本p所屬類別

若Ki=maxKi(p)，i=1，2，…，m，則判定樣本p屬于i類;若對一切i，Ki(p)≤0，則表示樣本p已不在所劃分的類別之內。

實例分析

醫院年收治病人數和多種因素有關，在此選取5個因素進行分析，資料見表1〔7〕。利用1981～1989年的數據建立可拓聚類預測模型的經典域物元和節域物元，將1990年的數據作為待測物元，對1990年的醫院年收治病人數進行區間預測。具體過程如下：

1.資料處理

某醫院1981～1990年收治病人數和可能影響因素的原始資料如表1所示，在此先計算出年收治病人數和各個影響因素的年增長率數據，這里的年增長率定義為該年的值與上一年的值之比〔3〕。

表1 某院1981～1990年收治病人數和可能影響因素的原始數據及年增長率

將1982～1989年的數據作為聚類樣本，1990年作為待測年。由表1數據可以看出，收治病人數的年增長率在0.90～1.16之間，將樣本數據按照收治病人數的年增長率 R 分為3類：I1：0.90＜R≤0.99，I2：0.99＜R≤1.08，I3：1.08＜R≤1.17。統計各類的樣本數并計算其因子(影響因素)均值，如表2所示。

2．確定經典域物元和節域物元及待測樣本物元

結合表1的年增長率數據和表2的因子均值數據構造各類的經典域物元以及節域物元，并確定待測樣本物元。通過觀察發現，各個因子的最大值均小于1.20，所以我們將節域的最大值確定為1.20，節域的最小值確定為各個因子的最小值，并且同一因子的各個經典域的區間并集為節域。

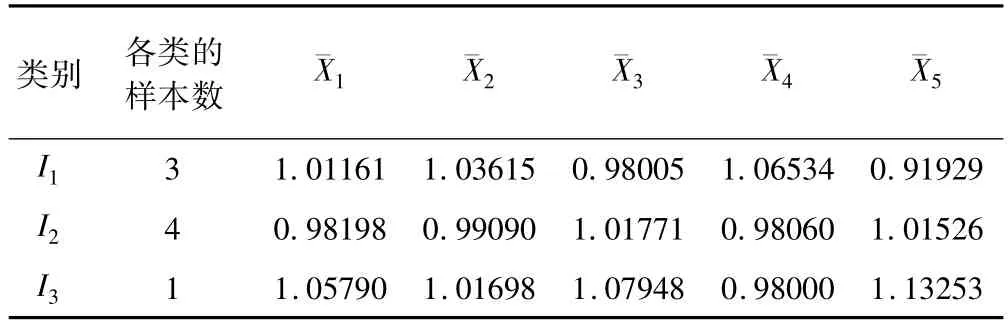
表2 醫院收治病人數年增長率的各類樣本數及因子均值

經典域物元為：

3.計算待測樣本對各類的關聯度

根據上述方法中的相關公式進行計算，最后結果如表3所示。因為X1，X2，X3和X5四個因子與年收治病人數成正向相關，即在一個區間內取值越大越好，所以我們選擇右側距最大值在端點b的公式進行計算，反之，因子X4選擇左側距最大值在端點a的公式進行計算。各個因子的權重用層次分析法來確定。

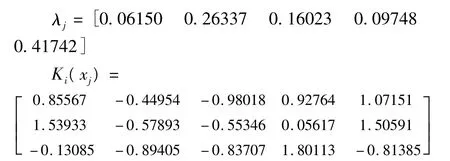
表3 待測樣本與各類的綜合關聯度及聚類預測結果

討 論

從關聯度和聚類預測結果可以看出，1990年的醫院收治病人數年增長率屬于第二類，即在0.99～1.08之間，而1990年的收治病人數實際年增長率為1.05971，恰好在第二類的范圍之內，所以用可拓聚類方法預測醫院年收治病人數是有效的。

用可拓學的理論和方法對醫院收治病人數進行預測是一種嘗試。它可以把多個影響因素綜合起來作為一個物元進行分析，其計算較為簡單，具有較強的實用性。而且該方法對樣本含量沒有嚴格的限制，預測精度不會受到樣本含量的影響。需要注意的是，該方法中關聯函數的選擇至關重要，不適合的關聯函數會導致錯誤的結論，另外，權系數的確定也是一個關鍵問題，所得到的權系數必須客觀、真實地反應實際情況。

1.蔡文.物元模型及其應用.北京：科學技術文獻出版社，1994.

2.周法蓮，郭秀花.可拓綜合評判在流腦發病率預測中的應用.數理醫藥學雜志，1998，11(1)：84-85.

3.高潔.可拓聚類預測方法及其在郵電業務總量預測中的應用.系統工程，2000，18(3)：73-77.

4.王超.可拓聚類模型在集裝箱生成量預測中的應用.物流科技，2008，10：34-36.

5.孫振球.醫學綜合評價方法及其應用.北京：化學工業出版社，2006：49-52.

6.呂榮愛，張鳳桃.綜合評價醫療效果與效率.中國衛生統計，2007，24(1)：90-91.

7.尹慧穎，劉勖.關聯度分析在醫院年收治病人數影響因素研究中的應用.中國醫院統計，1994，1(3)：137-140.