尾礦壩地震穩定性分析的區間模型及應用

董隴軍，趙國彥，宮鳳強，李志國

(中南大學 資源與安全工程學院，湖南 長沙，410083)

尾礦壩地震穩定性分析的區間模型及應用

董隴軍，趙國彥，宮鳳強，李志國

(中南大學 資源與安全工程學院，湖南 長沙，410083)

在尾礦壩地震穩定性分析中，為適應計算參數本身具有的隨機性和未確知性，將計算參數轉換成盲數形式；針對尾礦壩地震穩定的極限平衡分析問題，提出一種計算尾礦壩安全系數的新方法，并將該模型應用到某尾礦壩的地震穩定性分析中。實際分析結果表明：運用盲數運算法則可以計算穩定性系數在不同取值區間內的可信度，克服了傳統方法描述過于絕對化的問題，為判斷尾礦壩的穩定狀態提供了更全面的依據；該尾礦壩邊坡安全系數低于1.3的可能性為13%，即在發生烈度為Ⅶ度的地震時該尾礦壩安全的可能性為87%，失穩的可能性較小，與實際情況相吻合；盲數理論在尾礦壩地震穩定性分析中能更好地考慮參數的不確定性，完善了尾礦壩穩定性分析理論，為尾礦壩穩定性的分析提供了一條新的途徑。

尾礦壩工程；區間分析模型；盲數；地震穩定性；安全系數

尾礦壩工程中物理力學參數的選取是一個復雜的問題，存在大量的不確定性因素。穩定性分析所涉及的參數如黏聚力、內摩擦角、重度等往往不是定值，屬于不確定性信息。在傳統的尾礦壩地震穩定性的分析中，大多是按照經驗，忽略了計算參數的未確知性，將不確定性問題作為確定性問題考慮[1?7]。這些不確定

性信息包括隨機性、模糊性、灰性、未確知性等，相應的表達處理理論為概率統計、模糊數學、灰色數學、未確知數學等。如何全面考慮這些不確定性信息，提高計算的可靠性成為工程技術人員關心的問題，為此，許多研究者進行了大量地探索和研究[8?16]。劉開弟等[17]建立了未確知數學的理論體系，董隴軍等[5?9]將未確知測度理論發展到邊坡的地震穩定性分析、膨脹土等級判定、采空區危險性評價、圍巖穩定性分析等領域，取得了較好的效果。李朝甫等[2]將灰色系統理論用于滑坡位移分析中；徐衛亞等[3]將模糊集理論應用到邊坡穩定分析常用的極限平衡方法中，建立了穩定性分析的模糊計算方法；周建普等[4]將邊坡定值分析法與可靠性方法結合，考慮土性參數的變異性和不確定性。趙志峰等[1]將盲數理論應用到邊坡安全穩定分；析研究中。但是，這些研究大都是邊坡工程方面的，關于尾礦壩方面的研究較少。實際情況的限制和地質條件的復雜性使得很難對巖土體進行大量、準確的試驗，從而難以得到參數的準確值或概率分布，因此，在使用模糊數學等方法的過程中難以確定參數值合理的隸屬函數，給求解帶來了困難[1]。灰色理論中區間型灰數多是定義在一個區間內，可靠性分析方法也需要用大量的試驗資料來確定參數的變異性等不確定性指標。考慮到以上問題以及尾礦壩工程中參數的不確定性往往是多種不確定性(如模糊性和隨機性)的混合；因此，采用一種新的數學方法來表達多種信息的不確定性顯得尤為必要，即可以表示含有隨機性、模糊性、灰性及未確知性中2種或2種以上不確定性的信息[17]，在這方面盲數理論提供了較好的思路。在此，本文作者基于極限平衡分析方法及盲數理論建立尾礦壩地震穩定性分析的區間模型。

1 盲數的基本原理

盲數是未確知數學中用于表達和處理同時具有 2種或2種以上不確定性信息的數學工具[17]。

1.1 盲數的定義

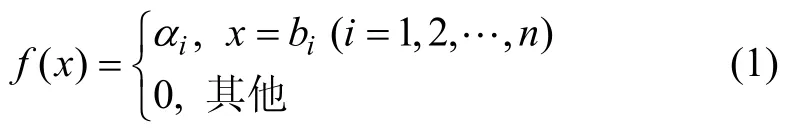
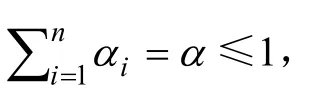
1.2 盲數的期望值

設a和b為實數，且a≤b。稱(a+b)/2為區間型灰數[a,b]的“心”，記作 Θ[a ,b]= (a+b)/2。若f(x)為盲數，且表達形式見式(1)，則盲數f(x)的期望值可以表示為

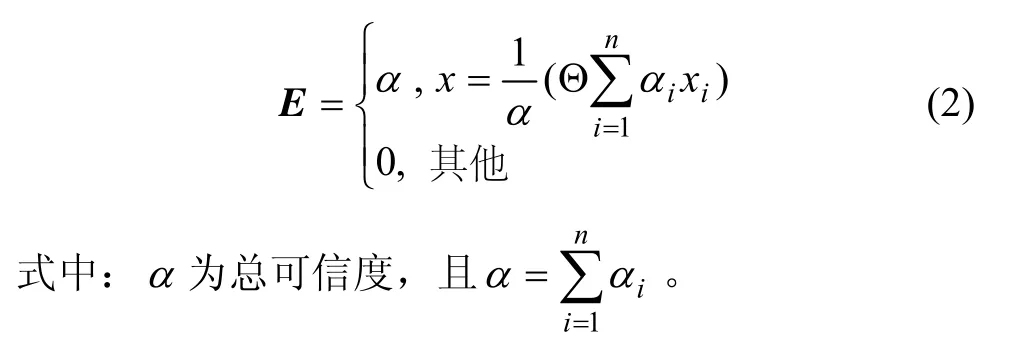
1.3 盲數的四則運算

設A與B為盲數，以加法為例，表1中稱A與B為可能值帶邊和矩陣，由小到大排列的實數列x1,x2, …,xk和y1,y2, …,ym分別稱為A與B的可能值序列，且分別稱為帶邊矩陣的縱邊和橫邊，互相垂直的直線分別稱為帶邊矩陣的橫軸和縱軸。

表1 A與B的可能值帶邊和矩陣Table 1 Sum matrix of A and B for probability

對照盲數加法定義，只需把和運算中的可能值帶邊和矩陣中的“和”改為相應的減、乘、除，從而把可能值帶邊和矩陣變為可能值帶邊減、乘、除矩陣，其他不變，即可得到未確知有理數積的定義。

1.4 盲數的可信度計算

表 2所示為A和B的可信度帶邊積矩陣，f(x1),f(x2), …,f(xk)和g(y1),g(y2), …,g(ym)分別稱為A和B的可信度序列，且分別稱為帶邊矩陣的縱邊和橫邊，互相垂直的直線分別稱為帶邊矩陣的橫軸和縱軸。

設A和B為盲數，分別表示為分布密度形式，即

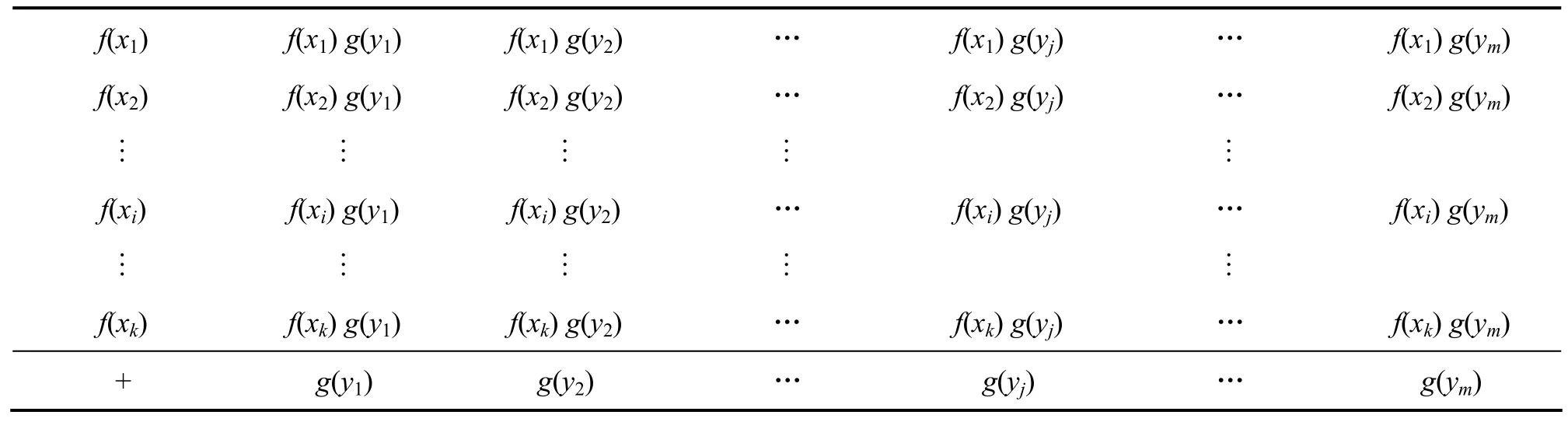
表2 A和B的可信度帶邊積矩陣Table 2 Product matrix of A and B for reliability

則事件A/B≥r的可信度表示為

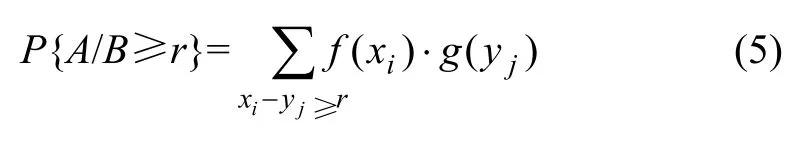
式中：B表示某一評價標準的分級閾值，一般為實數值形式；r是按實際問題要求而確定的某個已知實數。

2 地震荷載下尾礦壩穩定性分析的區間模型

尾礦壩的設計以及安全評價過程中均需要進行地震情況下的穩定性驗算。地震附加荷載可分解為水平附加荷載Ei和豎向附加荷載Ei′，計算公式分別為：

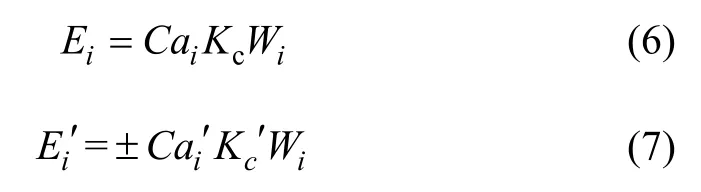
式中：C為地震綜合影響系數，常取用C=0.25；Wi為第i分條的質量；ai和ai′分別為水平與豎向地震加速度分布系數；Kc表示水平地震系數，為地面最大地震平均加速度與重力加速度之比，即 Kc=ai/g；表示豎向地震系數，=2Kc/3。

根據已有研究成果及規程[18]，對于土質或巖質邊坡，其變形破壞模式可按圓弧形破壞方式進行研究[1]。對尾礦壩而言，在其正常運行期間，浸潤線通常介于最危險滑動面和坡面之間，此時的尾礦壩穩定性驗算必須考慮浸潤線的影響，下面給出此種最常見情況下結構抗力A以及荷載效應B的計算公式。

為盡可能得到最精確的計算結果，需考慮動水力的作用。但是，動水力方向與垂直分條的豎直方向并不一致，故不能簡單地套用土條重力的處理方法。實際上，采用圓弧法分析邊坡穩定性本質上是考量滑動力矩與抗滑力矩的相對大小，考慮動水力時的尾礦壩結構抗力及荷載效應表達為抗滑力矩和滑動力矩。由于動水力的位置和作用方向均容易確定，因此，運用力矩進行處理還起到了簡化分析計算的效果。

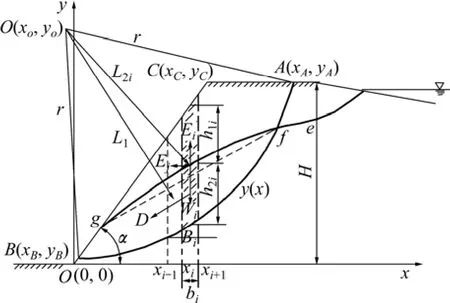
圖1 考慮地震和浸潤線作用的尾礦壩圓弧破壞剖面圖Fig.1 Slope section of arc of destruction considering impact of tailings dam infiltration and seism

如圖1所示，坡面方程為g(x)，圓弧形滑動面方程為y(x)，浸潤線efg的方程為ω(x)。設浸潤線、坡面以及圓弧滑動面所圍部分(fgBf)的面積為W，作用在這部分壩體上的動水力合力為D，則D的作用點在面積fgBf的形心，作用方向可假定與fg平行(如圖中箭頭所示)，動水力對滑動面圓心的力臂為L1。h1i和h2i分別表示采用垂直分條分析尾礦壩穩定性時浸潤線之上部分與浸潤線之下部分的土條長度。動水力可按下式計算：

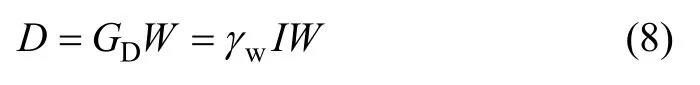
式中：GD表示作用在單位體積壩體上的動水力；w為水的重度；I為在面fgBf范圍內的水頭梯度平均值，可近似假設I等于fg連線的坡度。

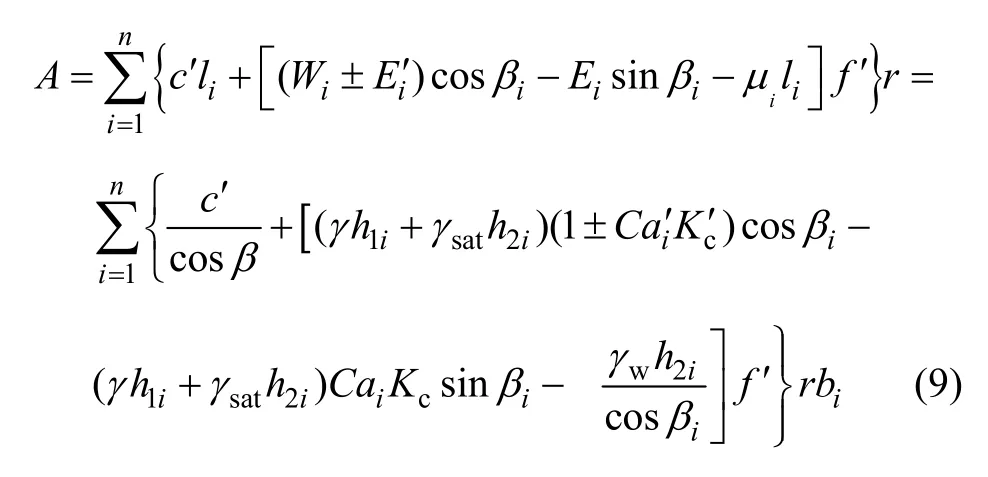
實際計算第i個土條的質量Wi時，若計算抗滑指標，則在浸潤線之下部分應考慮水的浮力作用；若計算滑動指標，則采用飽和容重。于是，考慮浸潤線后的尾礦壩結構抗力A的計算公式可表示為：式中：i為第i分條底面與水平面的夾角；li為第i分條底面弧長；Wi為第i分條質量； 和sat分別為尾礦天然重度和飽和重度；c′和f′分別為尾砂的有效粘聚力和有效內摩擦因數。

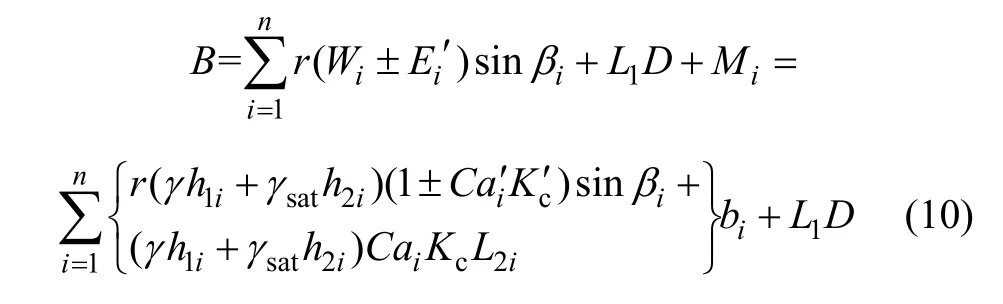
荷載效應B的計算公式可表示為：尾礦壩結構抗力A和荷載效應B的區間數分別為：

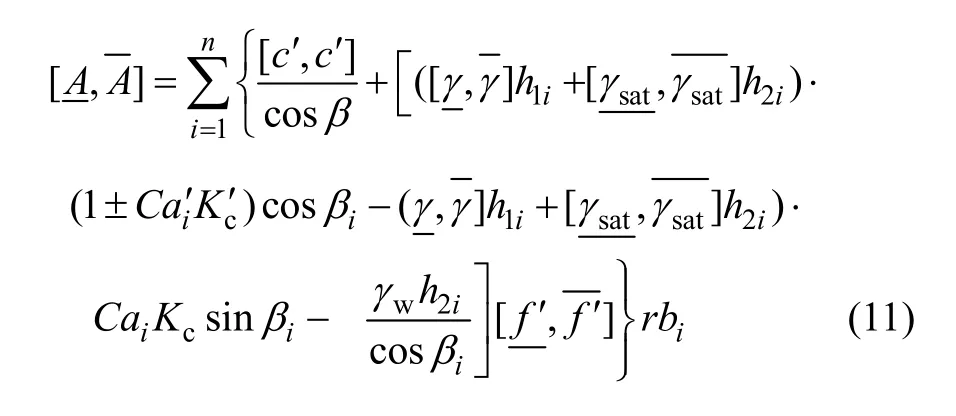
3 實例應用研究

某尾礦庫的等級為二等庫，堆積壩尾礦主要由尾細砂、尾粉砂、尾粉土和尾粉質黏土堆積而成，局部出現少量尾中砂。其地震基本烈度為Ⅶ度。采用上游法堆壩，堆積邊坡為1：6。最終總壩高210 m，最終堆積標高為1.3 km，總庫容為1.84×108m3，有效庫容為1.6×108m3，依據該尾礦壩的工程勘察報告，尾礦壩的物理力學參數見表3[16]。

根據式(11～13)，經計算得：尾礦壩安全系數F的取值介于0.91與1.10之間的可能性為3%；介于1.11與1.29之間的可能性為10%；介于1.30與1.97之間的可能性為53%；介于1.98與2.86之間可能性為27%；介于2.87與3.22之間的可能性為0.07。通過以上分析可見：該尾礦壩安全系數取值在1.30以下的可能性為13%。與傳統極限分析定值方法相比，這種表示方式全面地反映了在各個不同取值區間的可能性，避免了由于參數取值單一而造成的計算安全系數時的偏差，從而能更全面地判斷邊坡的安全穩定狀態，完善了尾礦壩穩定性分析理論。

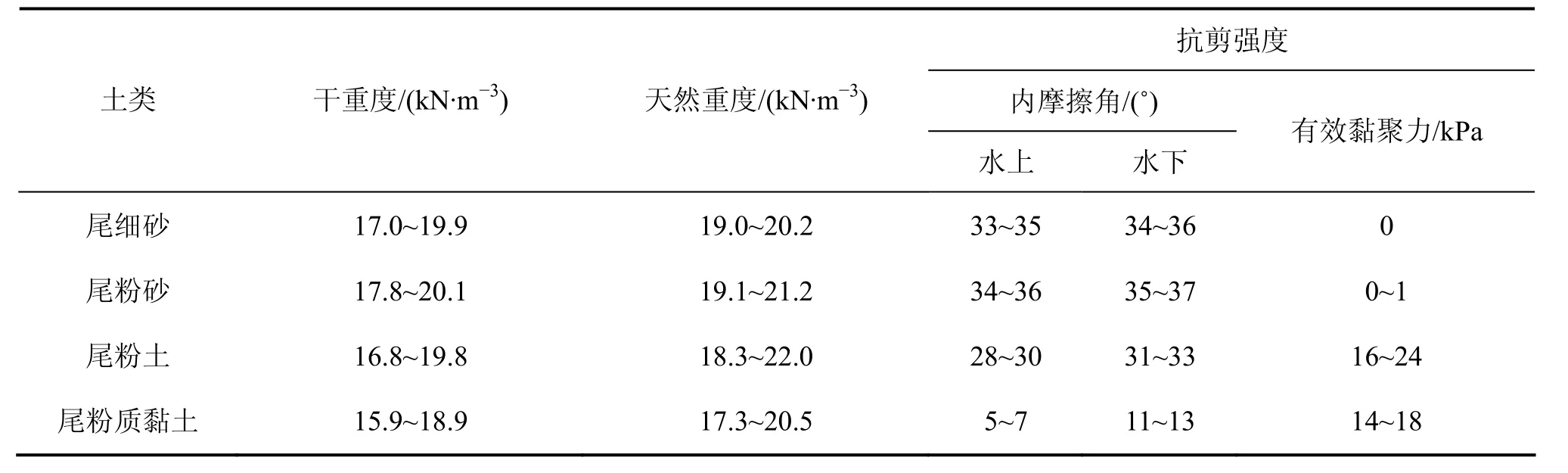
表3 尾礦壩物理力學參數Table 3 Physical and mechanical indicators of tailings dam

根據該尾礦壩邊坡工程的重要性等級和《規程》[18]，此尾礦壩邊坡的允許安全系數可以取為1.30。采用式(3)可以計算出F小于 1.30的概率為P(F＞1.3)=0.03+0.10=0.13=13%，由此可知，該尾礦壩邊坡安全系數低于1.3的可能性為13%，即在發生烈度為Ⅶ度的地震時該尾礦壩的安全性為87%，失穩的可能性較小，這一點與實際情況相吻合。在2008—08—30，該尾礦壩所在區域也發生了5.0級地震，壩體穩定性良好，未發生滑坡或失穩現象。盡管尾礦壩目前安全狀況較好，但也存在一定的風險，主管部門要重視尾礦壩的安全設施的維護，在后期筑壩的過程中應該采取更加合理的筑壩方式，增強壩體的穩定性。

4 結論

(1) 針對實際尾礦壩工程中參數的不確定性和試驗資料的有限性，基于極限平衡分析方法及盲數理論建立了尾礦壩穩定性分析的區間模型。該模型可以充分考慮分析中所涉及的計算參數的不確定性，將安全系數用盲數形式表達。

(2) 與傳統極限平衡分析方法相比，尾礦壩地震穩定性分析的區間模型可以實現將安全系數可能的各種情況用可信度表示，從而得到較為全面的結果，給安全穩定評判提供了較充分的依據，完善了尾礦壩穩定性分析理論。

(3) 該尾礦壩邊坡安全系數低于 1.3的可能性為13%，表明存在一定的風險，主管部門要重視尾礦壩的安全設施的維護，在后期筑壩的過程中應該改進的筑壩方式，加強浸潤線的觀測，以便增強壩體的穩定性。

(4) 盲數理論在在尾礦壩穩定性分析中的研究還只是初步嘗試，在今后的研究工作中，在如何更為有效地確定合理的力學參數取值區間、條分數等問題方面有待進一步研究，以增強該方法在實際工程中的適用性和可推廣性。

[1] 趙志峰, 徐衛亞. 基于盲數理論的邊坡安全穩定分析研究[J].巖土力學, 2007, 28(11): 2401?2404.

ZHAO Zhi-feng, XU Wei-ya. Slope stability analysis based on the blind data theory[J]. Rock and Soil Mechanics, 2007, 28(11):2401?2404.

[2] 李朝甫, 徐迎, 譚躍虎, 等. 灰色系統理論在滑坡位移分析中的應用[J]. 系統工程理論與實踐, 2002(2): 129?132.

LI Chao-fu, XU Ying, TAN Yue-hu, et al. Application of grey system theory to analyzing displacement information of slide[J].Systems Engineering Theory & Practice, 2002(2): 129?132.

[3] 徐衛亞, 蔣中明, 石安池. 基于模糊集理論的邊坡穩定性分析[J]. 巖土工程學報, 2003, 25(4): 409?413.

XU Wei-ya, JIANG Zhong-ming, SHI An-chi. Slope stability analysis using fuzzy sets theory[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 409?413.

[4] 周建普, 李獻民, 王永和. 黏土邊坡可靠性分析方法研究[J].湖南大學學報: 自然科學版, 2002, 29(5): 92?97.

ZHOU Jian-pu, LI Xian-min, WANG Yong-he. Research for method of reliability analysis for clayey soil slope[J]. Journal of Hunan University: Natural Sciences, 2002, 29(5): 92?97.

[5] 董隴軍, 王飛躍. 基于未確知測度的邊坡地震穩定性綜合評價[J]. 中國地質災害與防治學報, 2007, 18(4): 74?78.

DONG Long-jun, WANG Fei-yue. Comprehensive evaluation on seismic stability of slopes based on unascertained measurement[J]. The Chinese Journal of Geological Hazard and Control, 2007, 18(4): 74?78.

[6] DONG Long-jun, PENG Gang-jian, FU Yu-hua, et al.Unascertained measurement classifying model of goaf collapse prediction[J]. Journal of Coal Science & Engineering, 2008,12(2): 221?224.

[7] 董隴軍, 李夕兵, 宮鳳強. 膨脹土脹縮等級分類中的未確知均值聚類模型及應用[J]. 中南大學學報: 自然科學版, 2008,39(5): 1075?1080.

DONG Long-jun, LI Xi-bing, GONG Feng-qiang. Unascertained average clustering method for classification of grade of shrink and expansion for expansive soils and its application[J]. Journal of Central South University: Science and Technology, 2008,39(5): 1075?1080.

[8] 董隴軍, 李夕兵, 宮鳳強. 開采地面沉陷預測的未確知聚類預測模型[J]. 中國地質災害與防治學報, 2008, 19(2): 95?99.

DONG Long-jun, LI Xi-bing, GONG Feng-qiang.Comprehensive evaluation on seismic stability of slopes based on unascertained measurement[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(2): 95?99.

[9] DONG Long-jun, HU Da-tao, BAI Yun-fei. Unascertained average grade model for surrounding rock classification on hydraulic tunnels[C]//2008 International Symposium on Safety Science and Technology: Progress in Safety Science and Technology (Vol. VII). Beijing: Science Press, 2008: 2227?2231.

[10] 李文秀. 巖石力學中的 Fuzzy數學方法[J]. 力學學報, 1990,22(3): 328?336.

LI Wen-xiu. Fuzzy mathematic method in rock mechanics[J].Chinese Journal of Theoretical and Applied Mechanics, 1990,22(3): 328?336.

[11] 潘家錚. 建筑物的抗滑穩定和滑坡分析[M]. 北京: 水利出版社, 1980: 10?35.

PAN Jia-zheng. Stability and slope analysis of building[M].Beijing: Water Conservancy Press, 1980: 10?35.

[12] 張國祥, 劉寶琛. 潛在滑面理論及其在邊坡分析中的應用[M].長沙: 中南大學出版社, 2003: 5?20.

ZHANG Guo-xiang, LIU Bao-chen. Potentially sliding surface theory and application in the slope analysis[M]. Changsha:Central South University Press, 2003: 5?20.

[13] 王貴成, 曹平, 林杭, 等. 用灰色理論確定邊坡最優監測點及安全系數[J]. 中南大學學報: 自然科學版, 2007, 38(3):574?578.

WANG Gui-cheng, CAO Ping, LIN Hang, et al. Determination of optimum monitoring point of slope and safety factor using grey system theory[J]. Journal of Central South University:Science and Technology, 2007, 38(3): 574?578.

[14] 張世文, 王紅艷. 影響尾礦壩安全穩定性因素分析及對策[J].礦業工程, 2004, 2(2): 61?63.

ZHANG Shi-wen, WANG Hong-yan. Analysis of factors influencing stability of tailing dam and measures for improving dams stability[J]. Mining Engineering, 2004, 2(2): 61?63.

[15] 吳中如. 水工建筑物安全監控理論及其應用[M]. 南京: 河海大學出版社, 1990: 5?10.

WU Zhong-ru. Security monitoring theory and application of hydraulic structure[M]. Nanjing: Hohai University Press, 1990:5?10.

[16] 王飛躍. 基于不確定理論的尾礦壩穩定性分析及綜合評價研究[D]. 長沙: 中南大學土木建筑學院, 2008: 90?120.

WANG Fei-yue. Research on stability analysis and comprehensive assessment of taings dam based on the uncertainty theory[D]. Changsha: Central South University.College of Architecture and Civil Engineering, 2008: 90?120.

[17] 劉開弟, 吳和琴, 龐彥軍, 等. 不確定性信息數學處理及應用[M]. 北京: 科學出版社, 1999: 1?190.

LIU Kai-di, WU He-qin, PANG Yan-jun, et al. Mathematics processing of unascertained information and its application[M].Beijing: Science Press, 1999: 1?190.

[18] AQ 2006—2005. 尾礦庫安全技術規程[S].AQ 2006—2005. Technical specification for tailings dam safety[S].

(編輯 趙俊)

Interval analysis model of tailings dam seismic stability and its application

DONG Long-jun, ZHAO Guo-yan, GONG Feng-qiang, LI Zhi-guo

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The calculation parameters including the mixture of multi uncertainty were transformed to the blind data to express the uncertainty of the calculation parameters in the tailings dam engineering. The theory of blind information was applied to the rigid limiting equilibrium method for tailings dam seismic stability. A new method of safety factor was applied to the seismic stability analysis of a tailings dam. The results show that the corresponding confidence level of safety factor at different numerical value intervals can be calculated by blind data algorithms. The more comprehensive result is provided to judge the stability state of tailings dam consequently, overcoming the defect of absolutely definitive description in the traditional methods. The tailings dam slope safety factor is less than 1.3, and the corresponding possibility is 13%, indicating that the probability of the tailing dam safety is 87% in the event of seismic intensity of Ⅶdegrees, which is consistent with the actual situation. It is a new way to analyze seismic stability of tailing dams, and the result is more detailed and reliable.

tailings dam engineering; interval analysis model; blind data; seismic stability; safety factor

TV649；TD926.4

A

1672?7207(2011)01?0164?06

2010?09?06；

2010?12?21

國家自然科學基金資助項目(50934006)；中南大學學位論文創新項目(1343-74335000020)

董隴軍(1984?)，男，甘肅隴西人，博士研究生，從事采礦與巖土工程可靠性及災害控制研究；電話：18711191205；E-mail: csudlj@163.com