水濁度和提熱量對太陽池鹽梯度層穩(wěn)定性綜合影響

王 華， 孟凡茂， 孫文策， 鄒家寧

（1.大連理工大學(xué)能源與動力學(xué)院，遼寧大連 116024；2.河南理工大學(xué)機械與動力工程學(xué)院，河南焦作 454000；3.河南理工大學(xué)現(xiàn)代教育中心，河南焦作 454000）

0 引 言

鹽梯度太陽池由上、下對流層和位于中間的非對流層組成.在非對流層（NCZ，又稱為梯度層），密度隨深度增加而增加，反方向的溫度梯度產(chǎn)生的浮升力會使密度梯度減弱.下對流層（LCZ）是具有均一密度的儲熱層.如果忽略水平方向上的熱損失，下對流層的熱量僅以熱傳導(dǎo)的方式通過NCZ損失掉，所以NCZ相當(dāng)于一個透明的隔熱層.

太陽池是一個方便有效地長期儲存太陽能的熱利用系統(tǒng).梯度層（NCZ）將太陽池底部的熱鹽水與上面的冷淡水分離開，該層阻止收集到的太陽能向上層的熱損失.鹽梯度太陽池是一個典型的雙擴散系統(tǒng).如果NCZ的密度梯度大于溫度梯度引起的反方向密度梯度，那么系統(tǒng)處于穩(wěn)定的無對流狀態(tài)，即單純的導(dǎo)熱狀態(tài)；反之，雙擴散系統(tǒng)將不穩(wěn)定并導(dǎo)致對流發(fā)生.因此，太陽池梯度層的局部熱鹽通量之比很重要.所以有關(guān)NCZ的穩(wěn)定性標(biāo)準(zhǔn)都是關(guān)于鹽擴散率和熱擴散率之比的不同形式的表達(dá)式［1～4］.這些標(biāo)準(zhǔn)都是由分析方法推導(dǎo)出的簡單表達(dá)式.許多研究者對于考慮或者不考慮底部熱通量的熱鹽雙擴散系統(tǒng)穩(wěn)定性作了研究［5～7］.這些研究考慮了溫度和鹽度隨深度呈線性變化、強制性邊界條件以及底部熱源的熱通量為常數(shù)的情況.在這些研究中，關(guān)于系統(tǒng)穩(wěn)定性的常微分方程的解根據(jù)一系列未知系數(shù)確定.實際上太陽池內(nèi)的溫度和鹽度很少呈線性分布，強制邊界條件也不足以表達(dá)其邊界上狀況［8］.太陽池鹽梯度層的穩(wěn)定性問題是一個典型的非線性分岔問題.對于非線性常微分方程組，有兩種方法得到穩(wěn)定性，一種是在方程組中忽略二階項，采用Routh－Hurwitz準(zhǔn)則確定系統(tǒng)零解的穩(wěn)定性，這種方法被叫做線性穩(wěn)定性分析方法；另一種就是采用數(shù)值方法的非線性分析方法，這是因為非線性震蕩解不能夠采用線性的方法得到.文獻(xiàn)［8、9］研究了NCZ層中的二維熱鹽擴散的線性穩(wěn)定性.他們在研究中將NCZ看成是一個狹窄層或者無限擴展層.文獻(xiàn)［8］提出了一個簡單的數(shù)學(xué)方法解決梯度層問題，即采用Galerkin方法得到弱解方程的近似解，臨界狀態(tài)是關(guān)于Ra和Ras的表達(dá)式.

本文基于Giestas等［8、9］提出的數(shù)學(xué)公式，但不局限于其分析方法，討論系統(tǒng)從靜止無對流到不穩(wěn)定狀態(tài)的轉(zhuǎn)變條件，并研究池水的清澈情況與提熱量對梯度層穩(wěn)定性的影響.

1 控制方程的線性化

為了進(jìn)行動力穩(wěn)定性分析，將控制方程轉(zhuǎn)化成Galerkin形式的弱解方程.首先將非線性常微分方程組進(jìn)行線性化處理，描述不同鹽瑞利數(shù)Ras條件下的臨界穩(wěn)定性條件Rac對于提熱量f、消光系數(shù)μ的依賴關(guān)系.μ是被測溶液對光的吸收率的大小，溶液越渾濁，消光系數(shù)越大，對光的吸收率越大，而光的透射率越小.在二維穩(wěn)定性研究中，將NCZ看成是具有上下自由表面的長方體形厚平板，上下兩側(cè)具有固定的鹽濃度.控制方程如下：

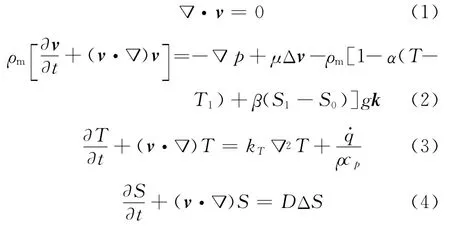
以上的方程（1）～（4）分別是連續(xù)方程、動量方程以及熱和鹽擴散方程.其中v是速度矢量；α、β分別是熱和鹽膨脹系數(shù)，單位分別是K－1、m3· kg－1；k T為熱擴散系數(shù)，m2·s－1；t為時間，s；T和S分別是溫度和鹽度，單位分別為K、kg·m－3；D為鹽擴散系數(shù)，m2·s－1.

在下界面上考慮傳導(dǎo)熱通量和上表面上的對流通量.邊界條件如下：

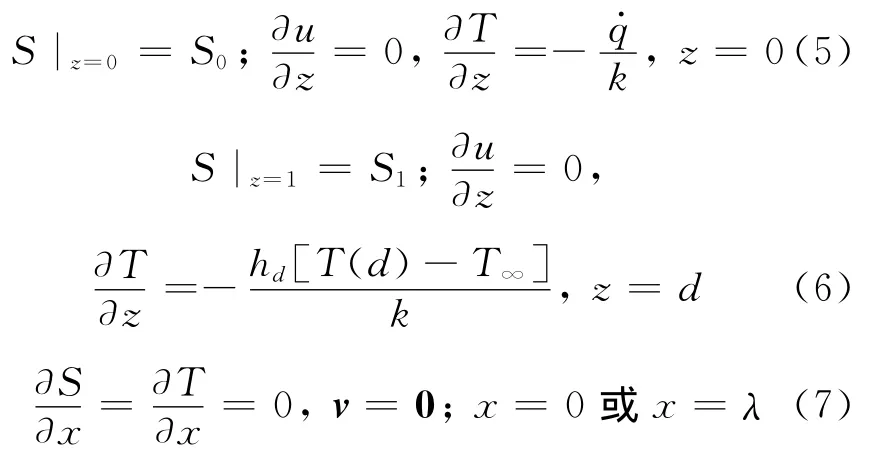
式中：k為梯度層導(dǎo)熱系數(shù)，W·m－1K－1；h d為梯度層上邊界與上對流層之間對流換熱系數(shù)，W· m－2K－1，d為NCZ厚度，自NCZ下邊界算起到上邊界的厚度.為了得到量綱一化方程，在流函數(shù)、溫度和鹽度項中加入擾動項，（ψ，T，S）代表擾動項和靜態(tài)項的總和.所以可以寫成

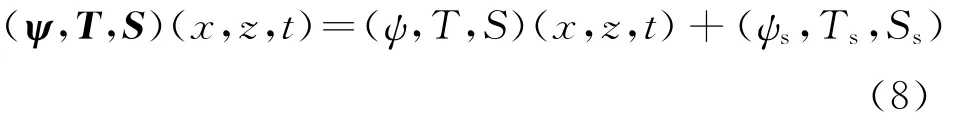
靜態(tài)項（ψs，Ts，Ss）可以在上述控制方程中根據(jù)v＝0和去掉時間項t得到.從而量綱一化控制方程可以寫成

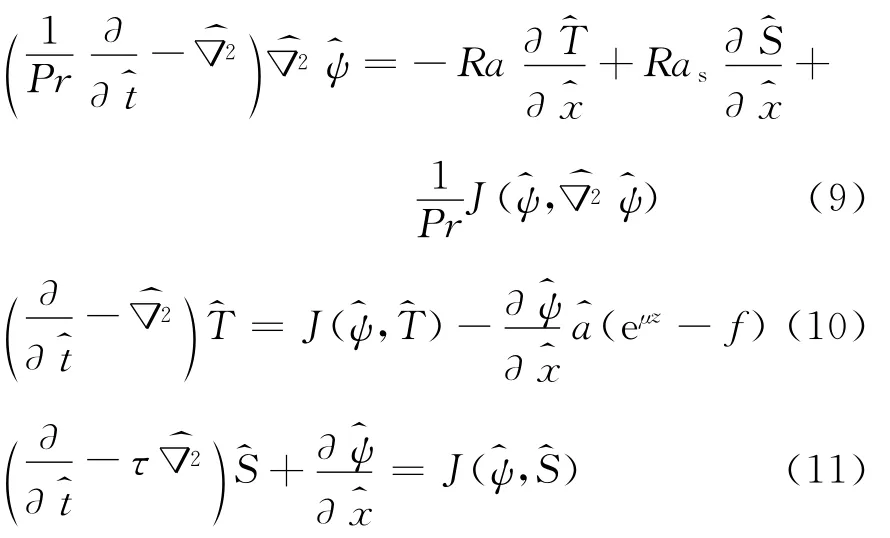
式中：Pr是Prandtl常數(shù)；τ為反Schmidt數(shù)，τ＝ks／k T；上標(biāo)“ ”表示量綱一化量，下文為了簡化，去掉上標(biāo)“ ”；Ra和Ras分別是熱和鹽瑞利數(shù)：

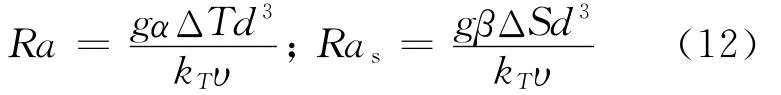
其中υ表示運動黏度，m2·s－1.在區(qū)域｛0＜x＜λ；0＜z＜1｝內(nèi)的邊界條件為

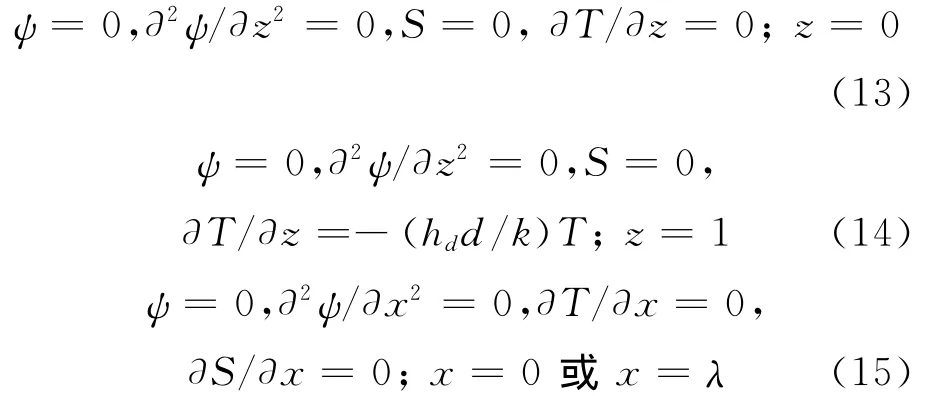
加權(quán)剩余Galerkin方法組成試驗多項式，假設(shè)待求變量等于以下多項式并且采用最小限度表示法，則有

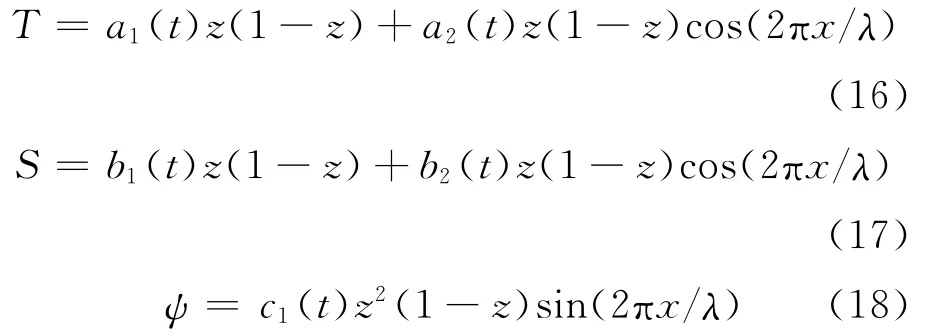
其中a1（t）、a2（t）、b1（t）、b2（t）、c1（t）都是時間t的未知函數(shù)，以下簡寫成a1、a2等，且這些函數(shù)形式都能夠滿足邊界條件.λ是x方向上的特征長度.將式（13）～（18）代入式（9）～（11）得到以下非線性常微分方程組：

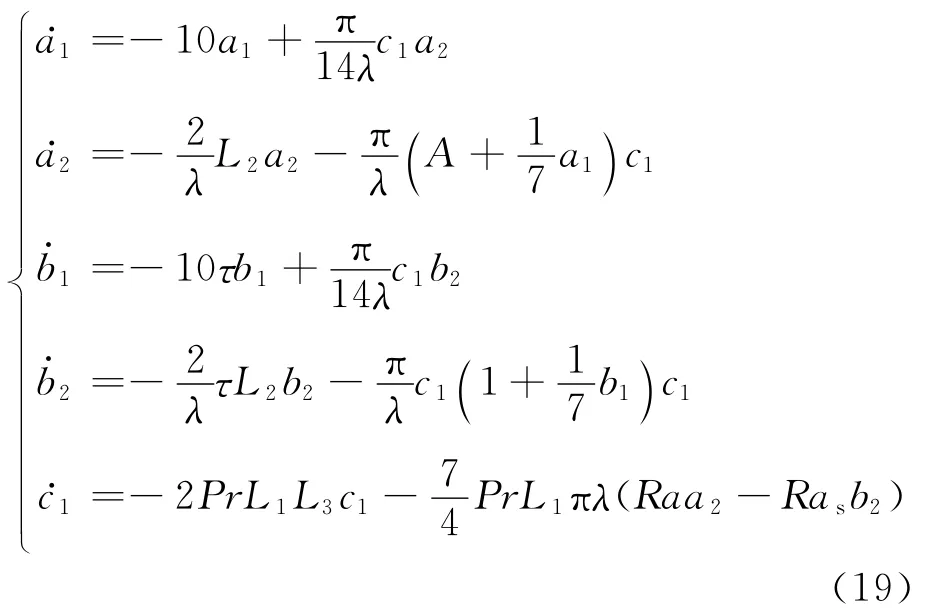
式中：上標(biāo)“·”表示時間的導(dǎo)數(shù)；L1、L2、L3是周期λ的函數(shù)；A是消光系數(shù)μ和提熱量f的函數(shù).關(guān)于L1、L2、L3和A，以及下文提到的Di、E等參數(shù)的表達(dá)式比較繁瑣，文中未給出.與洛侖茲系統(tǒng)相似，以上方程組雖然表面簡潔，但是具有極其復(fù)雜和有趣的動力學(xué)行為.下面主要討論該非線性系統(tǒng)的穩(wěn)定性.

2 線性穩(wěn)定性分析

2.1 漸進(jìn)穩(wěn)定性

針對非線性常微分方程組（19）的穩(wěn)定性分析十分困難，因此忽略所有的二階項，先進(jìn)行線性穩(wěn)定性分析.通過確定特征值實部的符號可以確定系統(tǒng)的穩(wěn)定性.如果特征值具有負(fù)的實部，那么方程組的零解是漸進(jìn)穩(wěn)定的.Routh－Hurwitz準(zhǔn)則可以用于確定特征值的符號.它給出所有的特征值多項式具有負(fù)的實部的充要條件.行列式方程的特征方程如下：

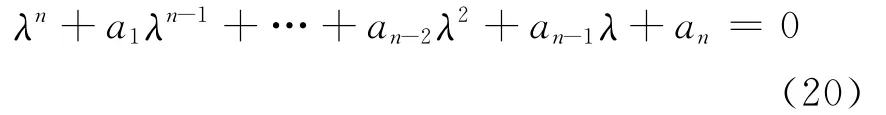
該準(zhǔn)則認(rèn)為如果下式成立，那么所有的根都具有負(fù)實部：

其中Ti是如下的連續(xù)行列式：

這樣，對方程（19）應(yīng)用此準(zhǔn)則，得到如下臨界穩(wěn)定性區(qū)域：

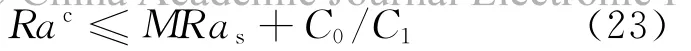
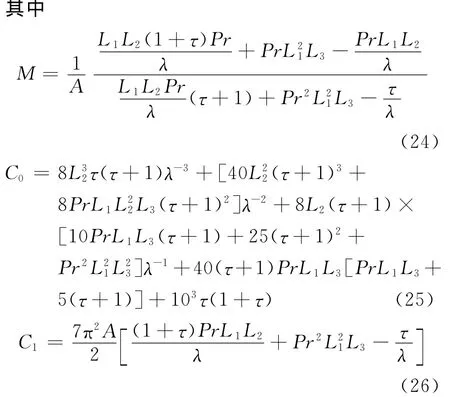
2.2 振 蕩

對方程（19）進(jìn)行線性化后的特征方程可以寫成如下五次多項式的形式：

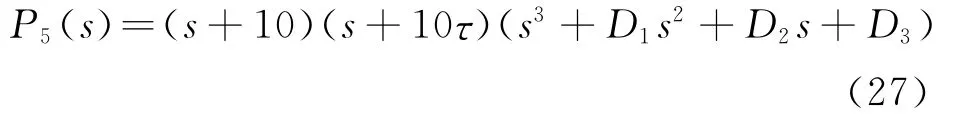
其中D1、D2和D3是k和τ的函數(shù)，適當(dāng)選擇D1、D2和D3的值使之滿足D1＝D3／D2，則式（27）右邊的三次多項式可以寫成如下形式：

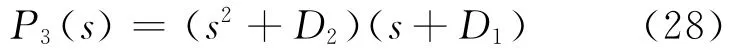
因此得到5個特征值：

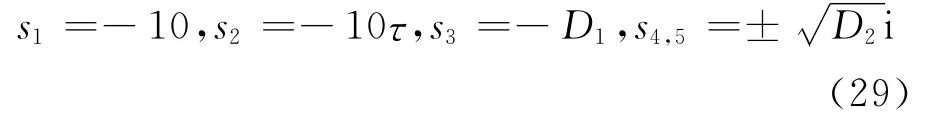
當(dāng)s＝0時，表示常幅對流狀態(tài)，將s＝0代入方程（27），可以得到系統(tǒng)發(fā)生常幅對流的區(qū)域：

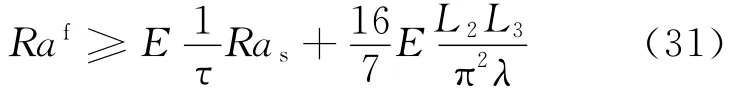
3 結(jié)果與討論

3.1 臨界條件

以上結(jié)果將Ra－Ras平面劃分為4個區(qū)域：穩(wěn)定性區(qū)域（靜止無對流）、振蕩區(qū)域、不穩(wěn)定對流區(qū)域和穩(wěn)定對流區(qū)域.圖1中的C、D、B、A分別代表以上4個區(qū)域.為了更全面地給出這些區(qū)域，圖1分別給出對數(shù)坐標(biāo)和常規(guī)坐標(biāo)下的圖形.對數(shù)坐標(biāo)下，圖1（a）坐標(biāo)長度平均地分給每個數(shù)量級.可見，除了在數(shù)量級102～104，臨界穩(wěn)定性Rac和振蕩開始的Rao1幾乎重合.然而，太陽池一般都具有很高的Ras.比較圖1中的兩幅圖可知，振蕩區(qū)域主要位于根據(jù)漸進(jìn)穩(wěn)定性確定的臨界穩(wěn)定性邊界之上.

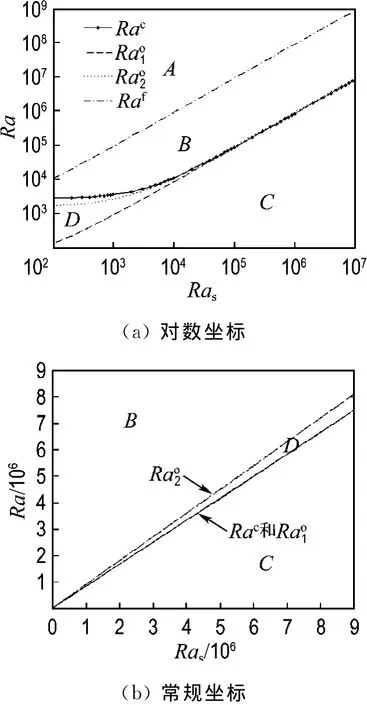
圖1 穩(wěn)定、振蕩和穩(wěn)定對流的臨界條件Fig.1 Marginal states for stable，oscillatory motions and steady convection

太陽池梯度層的臨界穩(wěn)定性對整個太陽池的效率起決定作用.本文根據(jù)Giestas等［8、9］對于控制方程的處理方法，采用Routh－Hurwitz準(zhǔn)則判斷漸進(jìn)穩(wěn)定性條件，而Giestas等在文獻(xiàn)［8］中將振蕩開始時作為臨界穩(wěn)定性條件，在文獻(xiàn)［9］中，其計算變參數(shù)情況下的臨界穩(wěn)定性條件.表1給出以上3個結(jié)果的比較，可見，本文結(jié)果與文獻(xiàn)［8］比較，二者接近，而與文獻(xiàn)［9］相差較大.

3.2 消光系數(shù)μ對Rac的影響

為研究消光系數(shù)對穩(wěn)定性（Rac）的影響，方程（23）中，因為只有A含有消光系數(shù)μ，若給定其他參數(shù)的值，比如τ＝0.01，λ＝2.129 8，保留A，得到

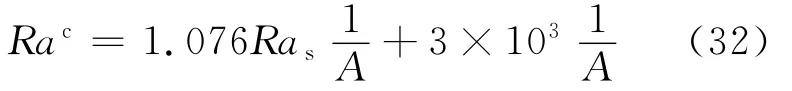
根據(jù)方程（32），在上對流層厚度以及提熱量一定的情況下，方程（32）可以寫成Rac＝F（Ras，μ）的形式，從而得到μ與Rac的函數(shù)關(guān)系.同理，固定μ，可將Rac寫成Ras和f的函數(shù)形式Rac＝g（Ras，f）.

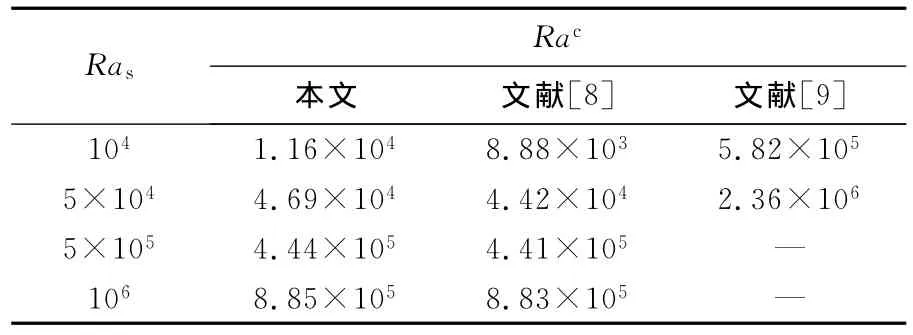
表1 本文的臨界穩(wěn)定性結(jié)果Rac與Giestas等研究結(jié)果的比較（Pr＝7，μ＝0.8，f＝0.5）Tab.1 Comparison of critical Rayleigh number determined by this paper and by Giestas，et al.（Pr＝7，μ＝0.8，f＝0.5）

由方程（32）可見，Rac只與A有關(guān)，因為A是μ和f的函數(shù)，下面分別研究μ和f對Rac的影響.μ代表水體的渾濁程度，若假定鹽梯度層的溫度梯度一定，不同μ情況下的計算結(jié)果反映梯度層于太陽輻射的吸收對該層穩(wěn)定性的影響，即在溫度梯度一定情況下，比較水濁度（消光系數(shù)μ）對穩(wěn)定性系數(shù)Rac影響.所以從消光系數(shù)本身和輻射吸收兩方面研究不同消光系數(shù)下的穩(wěn)定性，得出消光系數(shù)和提熱量對Rac的綜合影響.

（1）鹽梯度層靜態(tài)溫度分布

鹽梯度層一維穩(wěn)態(tài)導(dǎo)熱微分方程可以寫成

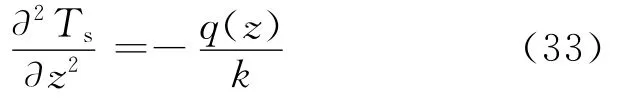
其中Ts表示穩(wěn)態(tài)情況下的溫度.鹽梯度層的邊界條件為

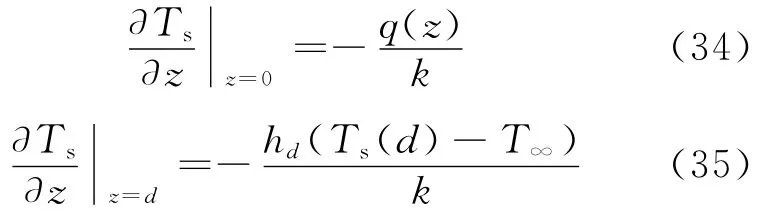
根據(jù)以上邊界條件，對方程（33）進(jìn)行積分，可以得到鹽梯度層的靜態(tài)溫度分布表達(dá)式：

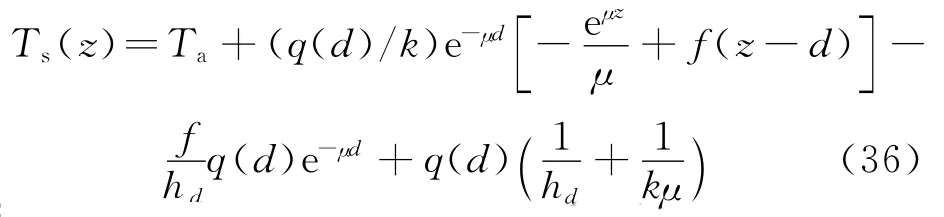
式中：Ta是環(huán)境溫度；q（d）是鹽梯度層上界面的輻射強度.根據(jù)式（36），可以求出梯度層的靜態(tài)溫度分布.

（2）結(jié)果與討論

假定鹽梯度太陽池符合以下參數(shù)條件：Ta＝293 K，k＝0.6 W·m－1K－1，h d＝100 W· m－2K－1，上對流層厚度dUCZ＝0.2 m，鹽梯度層厚度d＝1 m，qd＝50 W·m－2，f＝0.

圖2給出μ＝0.2，0.5和0.8時Rac變化曲線，可見穩(wěn)定性的臨界值Rac隨μ的變化很小，當(dāng)保持Ras不變，μ從0.2增加到0.5時，Rac降低1.8%；當(dāng)μ從0.5增加到0.8時，Rac降低1.2%.所以，對于鹽梯度一定的太陽池來說，其穩(wěn)定性Ra上限，受水體濁度影響很小；當(dāng)濁度增大后，Rac略有下降.對于同一Rac，μ越大，為保持梯度層穩(wěn)定狀態(tài)所需要的鹽梯度就越大.

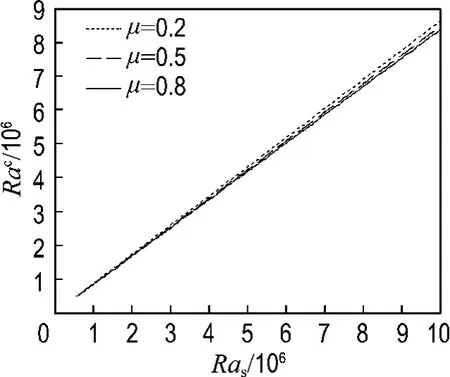
圖2 消光系數(shù)μ對于Rac的影響Fig.2 The influence ofμon Rac

圖3給出當(dāng)μ分別為0.2、0.5和0.8時，鹽梯度層一維靜態(tài)溫度分布情況.由圖3可見，由于水體透明度不同，即對太陽光的吸收率不同，μ＝0.2時的溫度曲線接近于直線，而μ＝0.8時，溫度曲線上部分彎曲.故在同樣情況下，清澈的水可容許鹽梯度層形成更大的溫度梯度；反之，水體越渾濁，梯度層上下界面之間的容許溫度差越小.綜合比較圖2和圖3，說明在同樣的鹽梯度情況下，水體越清澈，保持梯度層穩(wěn)定性所允許的最大溫度梯度越大.

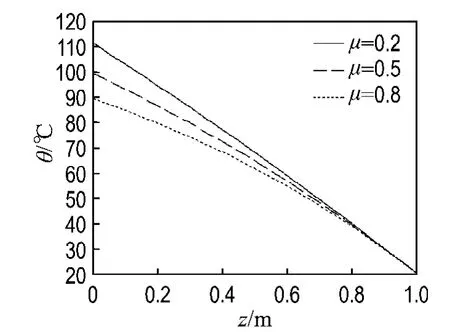
圖3 不同μ時穩(wěn)態(tài)鹽梯度層溫度曲線Fig.3 The steady NCZ temperature profiles for differentμ

3.3 消光系數(shù)μ與提熱量f對Rac的綜合影響

圖4給出Ras＝3×105，μ分別為0.8、0.6、0.4、0.2時，提熱量f從0增加到1.0時對應(yīng)的Rac.由圖4可見隨著提熱量增大，Rac增大，即提熱量增大，有利于保持鹽梯度層的穩(wěn)定性，這與文獻(xiàn)［8～10］中的結(jié)論一致.此外，由圖4可見，當(dāng)μ較小時，f的大小對Rac的影響較大；隨著μ的增大，f對Rac的影響逐漸減小.這說明當(dāng)梯度層比較清澈時，提熱量的大小對Rac的大小影響較大；當(dāng)池水比較渾濁時，提熱量的大小對Rac的影響較小.當(dāng)μ＝0.8，f＝0和μ＝0.2，f＝1.0時，對應(yīng)的Rac分別為2.17×105和7.33×105.從圖4還可以看出，各條曲線的交點在f＝0.65附近，在交點左側(cè)，對于同一f，μ越大，Rac越大；而在此交點的右側(cè)，μ越大，Rac越小.這表明存在某個提熱量大小，在其附近池水的清澈與否對梯度層的穩(wěn)定性臨界熱瑞利數(shù)大小影響很小；當(dāng)提熱量小于此值時，隨著梯度層內(nèi)濁度的增大，臨界熱瑞利數(shù)增大，系統(tǒng)趨向穩(wěn)定；當(dāng)提熱量大于此值時，隨著梯度層濁度的增大，臨界熱瑞利數(shù)減小，系統(tǒng)趨向于不穩(wěn)定.

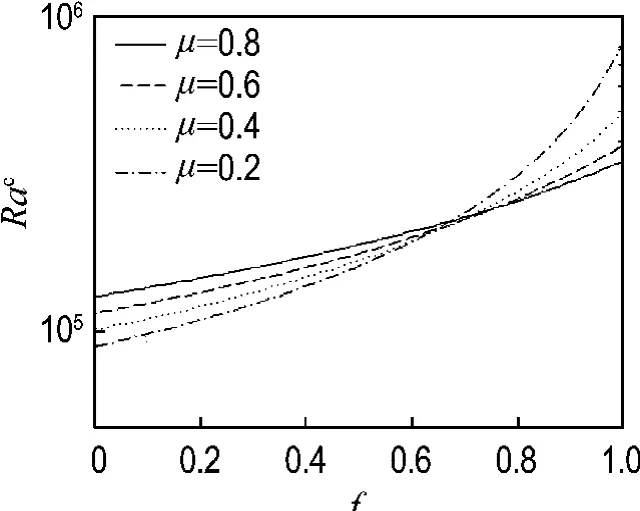
圖4 不同μ時，提熱量f對Rac的影響（Ras＝3×105）Fig.4 The influence of f andμon Rac（Ras＝3×105）

4 結(jié) 論

本文介紹了鹽梯度太陽池梯度層動力穩(wěn)定性的一種理論分析方法，即采用Galerkin方法將控制方程進(jìn)行簡化處理，忽略其中的非線性項，分析該線性系統(tǒng)的穩(wěn)定性.根據(jù)Routh－Hurwitz準(zhǔn)則判斷系統(tǒng)的漸進(jìn)穩(wěn)定性，然后將Ra－Ras平面劃分為4個不同的穩(wěn)定性區(qū)域.在此基礎(chǔ)上，分析了消光系數(shù)μ和提熱量f對于Rac的影響.結(jié)果表明，消光系數(shù)μ對Rac的影響很小，總之，太陽池梯度層穩(wěn)定性的熱瑞利數(shù)上限，受水體濁度的影響很小，當(dāng)濁度變大后，Rac略有下降.

［1］WEINBERGER H.The physics of a solar pond［J］.Solar Energy，1964，8（2）：45－55

［2］ROTHMEYER H.The soret effect and salt－gradient solar pond［J］.Solar Energy，1980，25（6）：567－568

［3］XU H.Laboratory studies on dynamical processes in salinity gradient solar pond［D］.Ohio：Ohio State University，1990：467－470

［4］ZANGRANDO F.On the hydrodynamics of salt gradient solar ponds［J］.Solar Energy，1991，46（6）：323－341

［5］VERONIS G.Effect of a stabilising gradient of solute on thermal convection［J］.Journal of Fluid Mechanics，1968，34（2）：315－336

［6］DA COSTA L N，KNOBLOCH E，WEISS N O.Oscillations in double－diffusive convection［J］.Journal of Fluid Mechanics，1981，100：25－43

［7］FINLAYSON A B.The Galerkin method applied to convective instability problems［J］.Journal of Fluid Mechanics，1968，33：201－208

［8］GIESTAS M，PINA H，JOYCE A.The influence of radiation absorption on solar ponds stability［J］.International Journal of Heat and Mass Transfer，1996，39（18）：3873－3885

［9］GIESTAS M，JOYCE A.The influence of nonconstant diffusivities on solar ponds stability［J］.International Journal of Heat and Mass Transfer，1997，40（18）：4379－4391

［10］REBAL K，MOJTABI A K，SAFI M J，etal.A linear stability study of the gradient zone of a solar pond［J］.Journal of Solar Energy Engineering，2006，128：383－393