超磁致伸縮薄膜懸臂梁靜力學分析

王福吉， 劉 巍， 賈振元， 劉慧芳， 趙顯嵩

（大連理工大學精密與特種加工教育部重點實驗室，遼寧大連 116024）

0 引 言

超磁致伸縮薄膜（GMF）是一種新型的功能材料，具有能量密度高、響應速度快和可實現無纜驅動等優點，在MEMS系統微執行器、傳感器以及其他功能元件中有著很好的應用前景.國內外科學家針對GMF進行了大量的研究工作，在其變形機理、有限元仿真和微執行器、傳感器設計上取得了很多成果［1～6］.

然而，目前仍然缺乏針對GMF的靜力學特性和動力學特性的分析研究，而對GMF的靜、動力學特性的準確分析是GMF微器件精確控制的基礎，所以，薄膜的靜、動力學特性研究對其進一步的應用研究有著非常重要的意義.

因此，本文選取福州大學采用磁控濺射方法制備的正負復合GMF懸臂梁作為研究對象，通過對其變形進行合理的簡化建立簡單實用的理論模型，繼而對以銅、聚酰亞胺為基片的兩種GMF懸臂梁進行靜力學特性實驗研究，以期為進一步研制開發GMF微型器件，推廣GMF微型器件在工程中的應用奠定基礎.

1 薄膜懸臂梁靜力學分析

1.1 彈性剛度的求解

如圖1所示，本文研究的GMF懸臂梁為雙層懸臂梁，即在基片上下表面均濺射磁致伸縮材料.其中，基片上表面濺射正磁致伸縮材料（Tb0.27Dy0.73）43Fe57，下表面濺射負磁致伸縮材料Sm1.9Fe2.這種正負復合薄膜懸臂梁較單層GMF懸臂梁具有更大的磁致伸縮力，可使懸臂梁結構產生更大的彎曲變形.GMF懸臂梁由不導磁的塑料夾具固定在驅動磁場中.當施加沿薄膜懸臂梁長度方向的激勵磁場時，正磁致伸縮材料因磁致伸縮效應沿磁化方向伸長，負磁致伸縮材料則縮短.這樣，正負磁致伸縮材料層對基片形成了彎矩進而使其發生彎曲變形.

圖1 GMF懸臂梁的結構Fig.1 GMF cantilever beam mechanism

磁致伸縮的本質是磁能和機械能之間的轉換過程，彈性剛度是衡量材料機械能量轉換能力的關鍵參數.項目研究的薄膜懸臂梁是由正負磁致伸縮材料濺射到基片上制備成的，3種材料各自的彈性常數都不同，因此在進行薄膜懸臂梁的靜力學分析前，必須對其有效彈性剛度進行分析計算.

將項目研究的正負復合GMF懸臂梁視為由正、負磁致伸縮單層膜和基片組成的復合梁.假設這3種材料的最大應力均不超過其比例極限，采用當量寬度法求解其中性軸位置和等效抗彎剛度［7］.這里以聚酰亞胺基片正負復合GMF懸臂梁為例說明當量截面法的求解過程，其結構如圖2（a）所示，選用聚酰亞胺基片的彈性模量為當量模量，則正、負磁致伸縮薄膜的當量寬度分別為bTb、bSm，如圖2（b）所示.根據應變與應力關系，可以得到GMF中性軸位置珔y和等效慣性矩珔I的計算式：

圖2 薄膜的當量寬度示意圖Fig.2 Sketch of equivalent film width

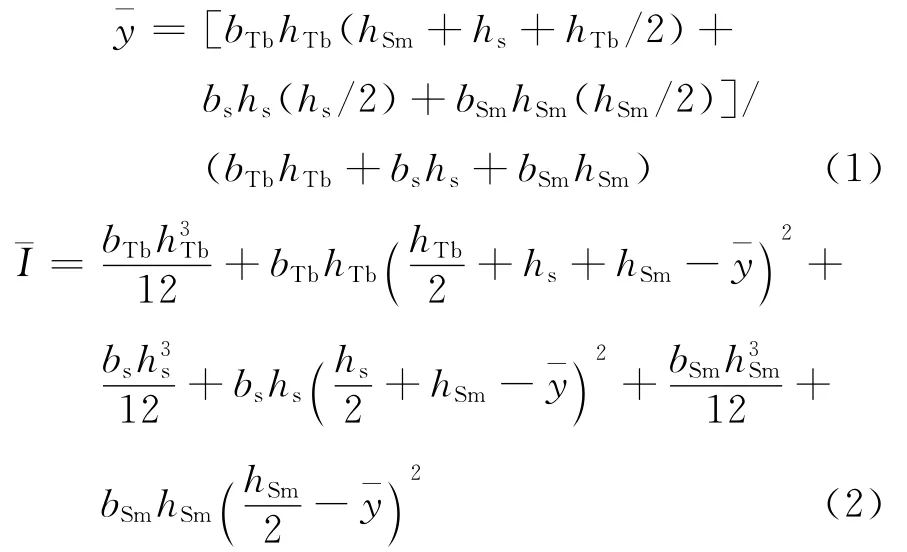
其中hTb、hSm、hs分別為正、負磁致伸縮薄膜和基片的當量厚度；bs為基片寬度，其值等于b.

由式（1）可知，正負復合GMF懸臂梁中性軸的位置與薄膜的寬度無關，分別將項目研究的聚酰亞胺基片、銅基片復合GMF材料的相關參數（見表1）代入式（1），得到以下結果：

①不同寬度的聚酰亞胺基片GMF懸臂梁實驗樣品的中性軸位置均為珔yPI≈20μm；

②不同寬度的銅基片GMF懸臂梁實驗樣品的中性軸位置均為珔yCu≈23μm.

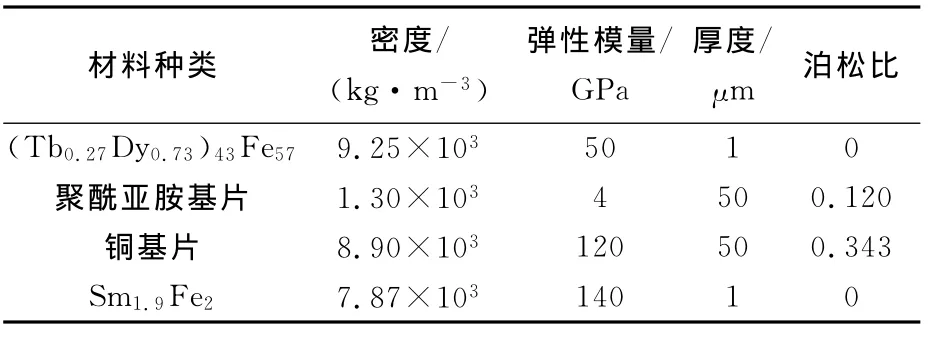
表1 正、負GMF靶材成分和基片的物理性能參數Tab.1 Physical parameters of positive and negative magnetostrictive GMF substrate and target material

在此基礎上，將聚酰亞胺基片、銅基片GMF懸臂梁實驗樣品尺寸參數（見表2）代入式（2），結合式（1）的計算結果得到了各種尺寸實驗樣品的等效慣性矩和等效抗彎剛度，如表2所示.

表2 各種實驗樣品的尺寸參數及等效慣性矩、等效剛度的計算結果Tab.2 Calculation results of experiment sample sizes，equivalent inertia moment and equivalent stiffness

1.2 撓曲線方程的求解

磁致伸縮過程是一個非常復雜的過程，磁學量與力學量的耦合系數是一個二階分量，這使得GMF磁－機械耦合過程的力學分析異常復雜［8］.本文采用直接考慮終端變形結果而忽略中間磁致伸縮過程的方法，來研究GMF磁致伸縮過程中力學參數的變化規律，以得出超磁致伸縮復合薄膜磁致伸縮效應作用的機理.

正負復合GMF懸臂梁的結構如圖1所示，取其中長度為dx的微分單元結構進行磁致過程中的受力分析［9］.假設磁致伸縮過程中，正、負磁致伸縮薄膜產生的磁致伸縮力是絕對均勻分布的，這時微分單元結構的受力情況如圖3所示.正磁致伸縮效應薄膜在微分單元兩側產生的拉應力分別為fTb（x）和fTb（x＋Δx），負磁致伸縮效應薄膜在微分單元兩側產生的壓應力分別為fSm（x）和fSm（x＋Δx）.

圖3 薄膜上微分單元的受力Fig.3 Stress of differential element on film

為了分析方便，本文引入集中力來代替正、負磁致伸縮薄膜產生的均布力.由于正、負磁致伸縮薄膜的彈性模量及產生力的大小不同，超磁致伸縮復合薄膜中性軸的位置已不在薄膜中心軸線上，其結果已在前面的計算中得出.進一步簡化微分單元結構上的受力情況，近似地將微分單元的受力等效為作用在單元中性軸的一個彎矩，進而可以得到微分單元所在懸臂梁截面應力分布情況，如圖4所示.根據以上的分析結果，可以近似地將懸臂梁式GMF產生的磁致伸縮力簡化為薄膜中性軸均布彎矩q的作用.

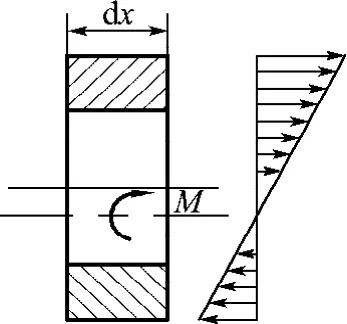
圖4 懸臂梁薄膜單元結構受力分析Fig.4 Structural stress analysis of GMF cantilever beam finite element

對于均布彎矩q作用的等截面GMF懸臂梁，根據材料力學的相關知識可導出其撓曲線微分方程的一般形式［10］：

其中ω（x）是撓曲線方程；M（x）是懸臂梁的彎矩方程.

分析GMF懸臂梁的受力變形情況，可得到其邊界條件為

求解上述微分方程，可以得出GMF懸臂梁的撓曲線方程為

為了驗證上述理論推導，本文首先從微觀角度對項目研制的GMF懸臂梁特性進行簡要分析.利用吉林大學研制的Jdm－13型振動磁強計進行測量，得到了項目研制的銅基片、聚酰亞胺基片的正負復合GMF平行易磁化軸方向的磁化曲線，如圖5所示（σ為單位質量磁矩，Hext為磁場強度）.

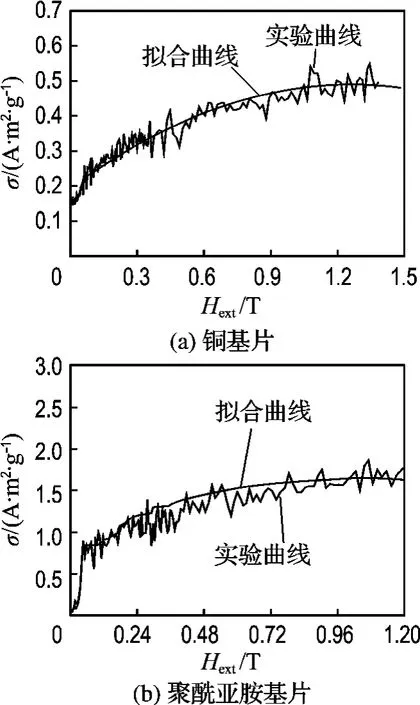
圖5 銅基片和聚酰亞胺基片GMF的初始磁化曲線Fig.5 Initial magnetization curves of Cu substrate thin film and polyimide substrate thin film

由圖5可以看出，聚酰亞胺基片GMF的磁致伸縮能力較強，其等效抗彎剛度較小，與前面求得的結果是相同的.此外，從圖上可以看出，這兩種GMF的初始磁化曲線呈現出了一定的線性關系.

2 薄膜懸臂梁的靜力學實驗

為了進一步驗證前面理論結果的正確性，項目設計了相應的實驗對3種不同結構尺寸的復合薄膜懸臂梁的變形情況進行研究.實驗系統結構如圖6所示，主要包括日本產高性能穩壓電源Bp4610、亥姆霍茲驅動線圈、美國產MicrotrakII激光測微儀、懸臂梁夾頭、美國產7030高斯計、示波器以及工作電腦等.其中亥姆霍茲驅動線圈為自制設備，主要參數有：內孔半徑18 mm，外孔半徑59.5 mm，單線圈寬度100 mm，線圈間距40 mm，單線圈匝數1 665，組合線圈電阻9.8Ω.

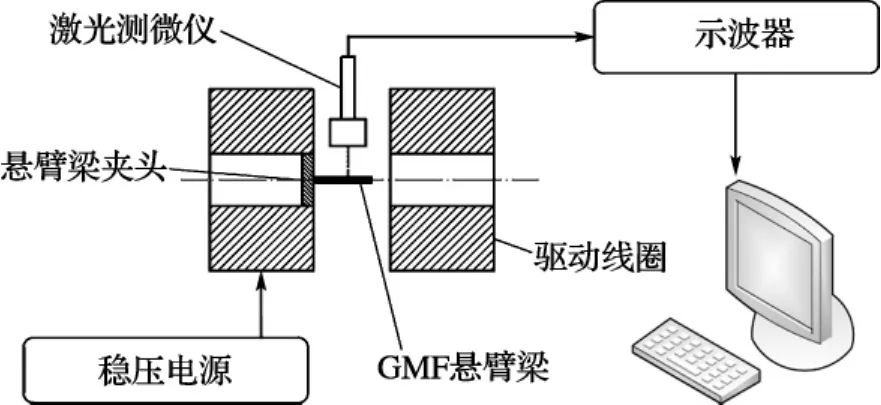
圖6 實驗裝置Fig.6 Experimental setup

實驗對懸臂梁在同一磁化狀態下不同位置的偏移量進行了測量，并通過曲線擬合得出了懸臂梁的撓曲線.在線圈驅動電壓為30 V，磁感應強度為27.4 m T時，分別得到聚酰亞胺基片、銅基片GMF懸臂梁的撓度實驗曲線與擬合曲線.其中，圖7（a）是長度38 mm、寬度3 mm的聚酰亞胺基片GMF懸臂梁磁致伸縮撓度的實驗曲線與擬合曲線.圖7（b）是長度30 mm、寬度3 mm的銅基片GMF懸臂梁磁致伸縮撓度的實驗曲線與擬合曲線.在驅動電壓30 V、驅動磁場192 mT時，得到長度30 mm、寬度3 mm的銅基片GMF懸臂梁磁致伸縮撓度的實驗曲線與擬合曲線，如圖7（c）所示.

從圖7中擬合曲線方程的形式可以看出，3種情況下GMF懸臂梁磁致伸縮撓度方程的形式均為δ（x）＝Ax3－Bx2的形式，其中A、B為與磁致伸縮效應有關的常數.擬合曲線形式與理論推導的超磁致伸縮復合薄膜懸臂梁撓度曲線方程式（7）的形式是一致的，可以證明理論分析方法和結論是正確的.在不考慮薄膜ΔE效應的前提下，根據懸臂梁超磁致伸縮復合薄膜結構撓度分析結果，可以認為薄膜的機械變形與薄膜產生的磁致伸縮力呈線性關系，即磁致伸縮過程中薄膜的磁學量與力學量呈一定的線性關系，研究的結果為動態磁致伸縮效應的進一步分析研究奠定了理論基礎.

圖7 GMF懸臂梁的撓度曲線Fig.7 Deflection curves of GMF cantilever beam

3 結 論

本文結合材料力學的相關理論，對GMF懸臂梁進行了靜力學特性分析.在求解不同材料雙層薄膜懸臂梁中性軸的基礎上，建立了其在靜態磁場作用下的撓曲線方程；進一步對不同基底材料和尺寸形狀的懸臂梁進行了實驗研究，結果表明本文的理論分析是正確的，所以通過材料力學的一般原理也可近似完成對GMF材料的理論分析.此外，本文的研究也表明磁致伸縮過程中薄膜的磁學量與力學量呈一定的線性關系，這一結論為動態磁致伸縮效應的進一步分析研究奠定了理論基礎.

［1］GUERRERO V H，WETHERHOLD R C.Strain and stress calculation in bulk magnetostrictive materials and thin films［J］.Journal of Magnetism and Magnetic Materials，2004，271（2－3）：190－206

［2］DEAN J，GIBBS M R J，SCHREFL T.Finiteelement analysis on cantilever beams coated with magnetostrictive material［J］.IEEE Transactions on Magnetics，2006，42（2）：283－288

［3］KAVIRAJ B，GHATAK S K.Simulation of stressimpedance effects in low magnetostrictive films［J］.Journal of Non－Crystalline Solids，2007，353（16－17）：1515－1520

［4］LEE H S，CHO C.Study on advanced multilayered magnetostrictive thin film coating techniques for MEMS application［J］.Journal of Materials Processing Technology，2008，201（1－3）：678－682

［5］ISHIYAMA K，YOKOTA C.Cantilevered actuator using magnetostrictive thin film［J］.Journal of Magnetism and Magnetic Materials，2008，320（20）：2481－2484

［6］TIERCELIN N，PREOBRAZHENSKY V，MORTET V.Thin film magnetoelectric composites near spin reorientation transition［J］.Journal of Magnetism and Magnetic Materials，2009，321（11）：1803－1807

［7］ROARK R J，YONG W C.應力應變公式［M］.北京：中國建筑工業出版社，1985

［8］王福吉.正負超磁致伸縮復合薄膜靜動態特性及控制關鍵技術［D］.大連：大連理工大學，2005

［9］劉廷柱，陳文良，陳立群.振動力學［M］.北京：高等教育出版社，1998

［10］王守新.材料力學［M］.大連：大連理工大學出版社，2004