最小二乘矩陣濾波器設計與性能分析

徐馳，韓磊，張書第，韓東

（海軍大連艦艇學院，遼寧大連 116018）

0 引言

矩陣濾波技術源于短數據濾波。傳統的FIR數字濾波器適用于數據長度較大的信號濾波，當信號數據長度較短時，由于FIR濾波器階數的制約，不能得到期望的濾波效果，矩陣濾波器能針對短數據長度信號設計，可在信號長度較短時得到所需的通阻帶響應效果［1－4］。根據矩陣濾波器的特點，它不僅可以用于短數據濾波，還可應用于陣列數據預處理。在陣列數據用于目標定向或定位算法之前濾波，可濾除或保留某一方位或扇面的信號及噪聲，能有效提高目標檢測能力及定位精度［5－10］。

在矩陣濾波器的設計方法中，Vaccaro［1－2］將濾波器對離散化的通帶響應誤差、阻帶響應和過渡帶振幅作為目標函數及約束條件構造凸規劃問題設計濾波矩陣;韓東［2］將Vaccaro的方法改進，得到了連續方式的解表達式，不僅提高了設計效率，也減少了計算量;Zhu［3－4］和鄢社鋒［6－7］設計了恒定阻帶抑制的矩陣濾波器，并將矩陣濾波器用于目標方位估計的預處理;自適應預濾波方法由Hassanien［8］提出，所構造最優化問題的目標函數中包含陣列數據協方差矩陣，也即包含輸入信號在各頻率的能量信息，利用此信息實現自適應濾波。以上這些矩陣濾波器的設計算法都存在一個共同的問題，即需要利用復雜的軟件或迭代算法才能給出矩陣濾波器的最優解，不適用于大陣元的濾波器設計問題。

本文在最小二乘矩陣濾波器設計的基礎上，利用奇異值分解給出了濾波器的簡化表達式及總體誤差，方法簡單，設計效率高。通過改變通帶阻帶位置、通帶阻帶帶寬及陣元數等條件，分析得出這些因素對最小二乘矩陣濾波器性能的影響趨勢，為矩陣濾波器的設計和應用提供參考。

1 最小二乘矩陣濾波器設計

考慮等間隔均勻線列陣，接收陣列數據為X（k） =AS（k）+N（k），設計一個M×M維矩陣濾波器H對均勻線列陣數據進行陣元域濾波，濾波輸出為:

式中:AH=HA;NH（k）=HN（k）。

對全空間的波達方向進行細分，細分點數為D，該矩陣濾波器對不同方向到達陣元的方向向量響應為

為使該矩陣濾波器保留感興趣方向的信號，濾除不感興趣方向的噪聲，并且限制過渡帶的輸出響應，可通過對不同的方向θi設計不同的k（θi），1≤i≤N值實現。

定義由全空間方向向量構成的陣列流形為X=［a（θ1，…，a（θD））］，維數為M×D，期望響應向量構成的期望陣列流形為Y=［k（θ1）a（θ1），…，k（θD）a（θD）］。所以，矩陣濾波器的設計問題就是求矩陣H，使HX=Y。

假設濾波器矩陣為

式中，hk=［hk1，hk2，…，hkM］，1≤k≤M是對應矩陣濾波器H的第k個行向量。令y=［h1，h2，…，hM］T，維數為M2×1，通過求解向量y就可以重構出矩陣濾波器H。

方向向量a（θj）經矩陣濾波器作用后，輸出響應Ha（θj）=k（θj）a（θj），1≤j≤D可轉化為如下的線性方程組:

通過矩陣變換及所構造的V和b，矩陣濾波器設計問題HX=Y轉化為一個線性方程組求解問題，

該線性方程組的線性方程數目為DM，未知數個數為M2。該線性方程組的解y受方程組系數矩陣V的秩決定，當rank（V）=M2且線性方程組行數目DM大于未知數個數M2時，該方程組存在最小二乘解。

求矩陣V的秩。重排矩陣的各行不改變矩陣的秩，對矩陣V重排，可得:

式中，X為Vandermonde矩陣，當D＞M時，該矩陣列滿秩，反之則行滿秩。即

通常，對接收陣列數據進行矩陣濾波處理，對通帶、過渡帶、阻帶的離散化向量數目總和D遠大于接收陣陣元數目M，這說明矩陣V是列滿秩的，即線性方程組Vy=b是超定的，可利用誤差平方和最小求出該方程組的最小二乘解。

通過以西北師大的研究生新媒體運營為例進行的受眾分析研究，我們發現了存在于高校新媒體運營中的一些問題，了解到受眾與平臺之間的重要聯系，只有在明確受眾群體的需求上，進行針對受眾的內容創新是新媒體運營發展的關鍵。以上問題及相應的可行性運營建議，不僅適用于西北師大研究生會新媒體運營，對于甘肅各高校研究生新媒體運營平臺也具有一定的借鑒意義。

式中:（·）H為矩陣共軛轉置;（·）－1為方陣求逆矩陣。（VHV）－1VH是V的左偽逆矩陣，利用求得的y就可以重構出矩陣濾波器H。

由前面構造可知，V的維數為DM×M2，b的維數為DM×1，所以利用V的左偽逆與b的乘積求解y計算量非常大，影響了運算效率，結果的準確性受運算軟件的制約。通過化簡可得到矩陣濾波器最小二乘解的陣列流形矩陣運算形式。

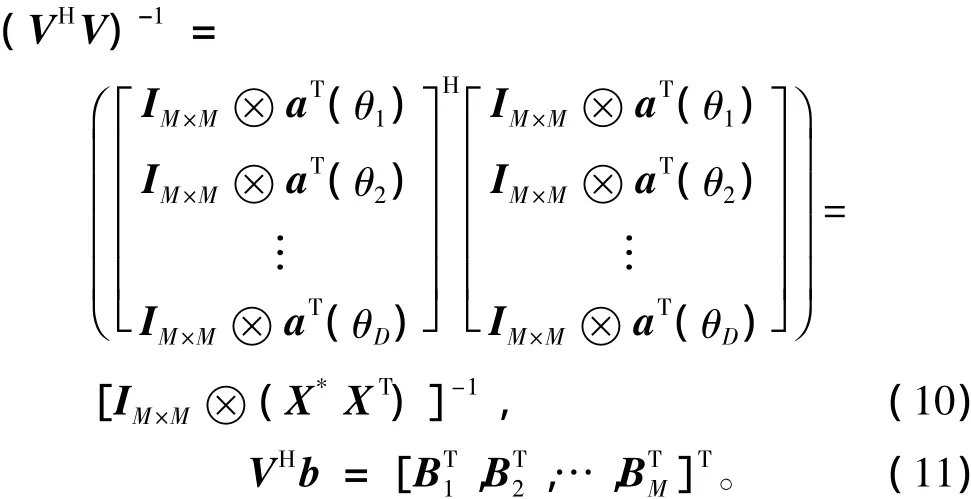
式中，Bi（1≤i≤M）的維數為M×1，且

利用式（14）構造矩陣W=［B1，B2，…，BM］，維數為M×M。矩陣W與矩陣X，Y的關系為

（·）*表示矩陣共軛。合并式（13）和式（14），有

重排向量y，可得:

即矩陣濾波器H等于期望陣列流形Y與原陣列流形X的右偽逆XH（XXH）－1的乘積。可以通過期望陣列流形中波達方向系數k（θj），1≤j≤D的設置得到不同類型的矩陣濾波器。

2 奇異值分解濾波器誤差分析

本節利用奇異值分解給出最小二乘矩陣濾波器的簡化運算形式，并分析濾波器響應整體誤差。上節給出了最小二乘矩陣濾波器的數值解，即矩陣濾波器H等于期望陣列流形Y與原陣列流形X的右偽逆XH（XXH）－1的乘積。現利用矩陣奇異值分解簡化式（15）的濾波器設計。由前述已知rank（X）=M，假設陣列流形的奇異值分解為

其中，U∈CM×M，Q∈CD×D，U和Q都是酉矩陣，ΣX=［Σ1，0M×（D－M）］∈CM×D，Σ1=diag（r1，r2，…，rM）∈RM×M。由于rank（X）=M，因此ri≠0，i=1，…，M，利用奇異值分解可得:

濾波輸出總體誤差為:

3 仿真分析

最小二乘矩陣濾波器的性能主要與濾波器通帶阻帶位置、通帶阻帶帶寬及陣元數等因素有關。通過計算機仿真，分析各因素對矩陣濾波器歸一化總體均方誤差的影響，為矩陣濾波器設計和使用提供參考。歸一化總體均方誤差值可以度量矩陣濾波器對空間各向信號的濾波效果，定義歸一化總體均方誤差為:

其中，ΩP和ΩS分別表示通帶區域和阻帶區域。最小二乘矩陣濾波器的總體誤差與通帶位置有關。下面通過計算機仿真分析研究最小二乘矩陣濾波器隨通帶位置變化的響應及歸一化總體均方誤差。

假設水聽器線列陣陣元間隔為半波長且均勻分布，陣元個數為30。下面設計1個單通帶矩陣濾波器，通帶的帶寬固定為30°。通帶、阻帶和過渡帶的離散化采樣間隔均設置為1°。給出通帶中心位置為10°，15°，30°，45°，60°時矩陣濾波器的空域響應

從圖1的仿真結果可知，在固定通帶寬度和陣元數的情況下，通帶處于正橫位置時，最小二乘矩陣濾波器具有最佳的空域響應效果。隨著通帶中心位置向端首或端尾的外移，通帶響應誤差及阻帶響應誤差隨之增大。圖2給出了不同陣元數情況下，最小二乘矩陣濾波器總體均方誤差隨通帶中心位置變化的趨勢。由仿真結果可知，在相同陣元數情況下，隨通帶外移，歸一化總體均方誤差增大。在固定通帶中心位置情況下，隨陣元數的增加，歸一化總體均方誤差減少。

矩陣濾波器的響應效果不僅與通帶位置有關，還與通帶寬度有關，假設通帶中心位置固定為0°，通帶寬度逐漸增大，觀察此時的矩陣濾波器響應效果和歸一化總體均方誤差。圖3中，分別給出了陣元數為30時通帶寬度為10°，30°，50°，70°和90°的矩陣濾波器響應和誤差圖。從圖3可知，隨通帶寬度的增加，通帶誤差和阻帶響應隨之變化。圖4給出了陣元數為20，40，60，80和100時，通帶寬度變化的矩陣濾波器歸一化總體均方誤差，從仿真結果可知，隨通帶寬度的增加，歸一化總體均方誤差先增大后減小。

從矩陣濾波器的通帶位置及通帶寬度仿真可知，在不同陣元數情況下，矩陣濾波器所得的歸一化總體均方誤差有不同的結果，隨陣元數的增加，總體誤差都隨之減小。現固定通帶位置和通帶寬度，觀察陣元數對最小二乘矩陣濾波器性能影響的大小。假設水聽器線列陣陣元間隔為半波長且均勻分布。設置通帶扇面［－15°，15°］，阻帶扇面為［－90°，－15°）∪（15°，90°］，離散化采樣點間隔為0.1°。濾波器響應和誤差效果如圖5所示。

從圖5的仿真結果可知，隨陣元數目的增加，最小二乘矩陣濾波器通帶和阻帶的誤差都在下降，當陣元個數從20變化到100時，矩陣濾波器的通帶失真逐漸減小，通帶誤差從－15 dB變化到－20 dB;而阻帶衰減也逐漸增大，從－20 dB左右增大到－30 dB左右。從圖6的仿真結果可知，隨陣元個數從10增加到100時，最小二乘矩陣濾波器的歸一化總體均方誤差呈拋物線下降。仿真結果說明，對于最小二乘矩陣濾波器的設計，陣元個數越多所得的濾波器響應效果越好，進而具有更好地陣列信號空域預處理能力。

4 結語

本文在最小二乘矩陣濾波器設計的基礎上，利用奇異值分解給出了濾波器的簡化表達式及總體誤差。通過改變通帶阻帶位置、通帶阻帶帶寬及陣元數等條件，分析得出這些因素對最小二乘矩陣濾波器性能的影響趨勢，為矩陣濾波器的設計和應用提供參考。

［1］VACCARO R J，HARRISON B F．Optimal matrix-filter design［J］．IEEE Trans．Signal Processing，1996，44（3）: 705－709．

［2］HAN Dong，ZHANG Xin-hua．Optimal matrix filter design with application to filtering short data records［J］．IEEE Signal Processing Letters，2010，17（5）:521－524．

［3］ZHU Z W，WANG S，LEUNG H，et al．Matrix filter design using semi-infinite programming with application to DOA estimation［J］．IEEE Trans．Signal Processing，2000，48 （1）:267－271．

［4］WANG Shi，ZHUZhi-wen，LEUNGH．Semi-infinite optimization technique for the design of matrix filters［J］．Statistical Signal and Array Processing，1998，9（14）:204－207．

［5］韓東，章新華，康春玉，李軍．零點約束矩陣濾波設計［J］．聲學學報，2010，35（3）:353－358．

［6］VACCARO R J，CHHETRI A，HARRISON B F．Matrix filter design for passive sonar interference suppression［J］．J Acoustic Soc Am，2004，115（6）:3010－3020．

［7］鄢社鋒，侯朝煥，馬曉川．矩陣空域預濾波目標方位估計［J］．聲學學報，2007，32（2）:151－157．

［8］鄢社鋒，馬遠良．匹配場噪聲抑制:廣義空域濾波方法［J］．科學通報，2004，49（18）:1909－1912．

［9］MACINNES C S．Sourcelocalizationusingsubspace estimation and spatial filtering［J］．IEEE J．Ocean．Eng．2004，29（2）:488－497．

［10］HASSANIEN A，ELKADER S A，GERSHMAN A B，et al．Convex optimization based beam-space preprocessing with improved robustness against uut-of-sector sources［J］．IEEE Trans．Signal Processing，2006，54（5）:1587－1595．

［11］袁亞湘，孫文瑜．最優化理論與方法［M］．北京:科學出版社，1997．