運用Gibbs抽樣解決數據缺失

王 怡，周 力

（東華大學 旭日工商管理學院,上海 200051）

1 傳統缺失值處理方法

目前國內廣泛接受的對于數據倉庫缺失值處理方法有6種處理缺失值的方法：

(1)忽略元組：當缺少類標號時通常這樣做（假定挖掘任務涉及分類）。除非元組有多個屬性缺少值，否則該方法不是很有效。當每個屬性缺少值的百分比變化很大時，它的性能特別差。

(2)人工填寫缺失值：一般，該方法很費時，并且當數據集很大，缺少很多值時，該方法可能行不通。

(3)使用一個全局常量填充缺失值：將缺失的屬性值用同一個常數 （如 “Unknown”或-∞）替換。如果缺失值都用“Unknown”替換，則挖掘程序可能誤以為它們形成了一個有等趣的概念，因為它們都具有相同的值“Unknown”。因此，盡管該方法簡單，但是它并不十分可靠。

(4)使用屬性的均值填充缺失值。

(5)使用與給定元組屬同一類的所有樣本的屬性均值。

(6)使用最可能的值填充空缺值：可以用回歸、基于推導的使用貝葉斯形式化方法或判定書歸納確定。

方法3～6由于沒有使用總體的信息，可能致使數據偏置，不能正確的反映數據總體情況。另外，雖然方法6目前最為常用，因為與其他方法相比，它使用現存數據的多數信息來推測空缺值，如果所有有關系的值均缺失，無法根據現有值產生其他值的情況，方法6也就失效了。因此可以說目前提出的方法并不能很好的解決數據缺失的問題。

總而言之，雖然目前已經提出了一些應用于數據預處理的方法，但是在對缺失數據進行處理的問題上都沒有理想的解決辦法。因而本文將對以上兩個問題的解決進行探討，下面就對研究思路和研究內容進行詳細闡述。

2 Gibbs抽樣基本步驟介紹

Gibbs抽樣是一種潛在應用非常廣泛的仿真工具，1990年該工具發表后立即得到了廣泛的響應。Gibbs抽樣表現為一個Markov鏈形式的Monte Carlo方法，其良好的性質可用于許多隨機系統的分析、多元分布的隨機數產生。下面介紹Gibbs抽樣的基本原理。

假設X,Y等大寫字母表示隨機變量或隨機向量；[X], [Y]則代表其相應的概率分布；[X|Y],[Y|X]表示條件分布。

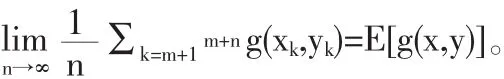
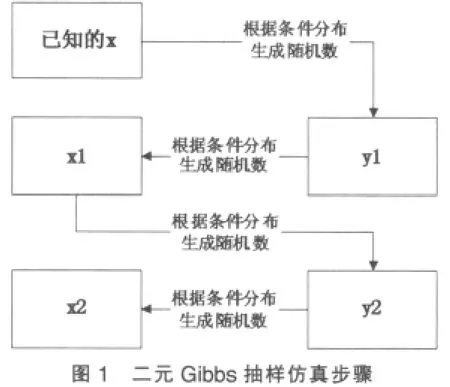
Step 1任意選取X的一個可能取值點x1，根據[Y|X=x1]產生隨機數y1，隨機數對(x1,y1)成為隨機點列{(x,y)n}中第一個點；

Step 2根據[X|Y=y1]產生隨機數x2，根據[Y|X=x2]產生隨機數y2，隨機數對(x2,y2)成為隨機點列{(x,y)n}中第二個點；

Step 3重復以上過程n次，我們即能得到所需要的隨機點列{(x,y)n}。

推廣到一般情況，如果條件分布

需要強調的是，Gibbs抽樣的先決條件是部分特定條件分布已知，稱為“條件分布充足條件”即FCDC，也就是上面提到的二元情況中的[X|Y]和[Y|X]，以及一般情況中的，[X1,X2,…,Xk]，[X2,X1,X3,…,Xk],…,[Xk,X1,…,Xk-1]。

3 實證分析

（1）數據準備

以某項統計調查學生基本信息的數據作為原始數據，該數據共有300條記錄。選擇其中學生的性別和家庭情況兩列作為Gibbs抽樣仿真中的兩個變量，這兩列的數據是離散的，性別中1代表女生，0代表男生。而家庭條件中1代表單親家庭，2代表他人照顧，3代表雙親家庭。

將后150條記錄的數據去除，造成全數據缺失的情況。去除的數據仍需保存，以便在使用Gibbs抽樣后對數據的模擬情況進行評價。

（2）獲得條件分布

對信息完整的前150條記錄進行統計，利用所得到的統計數據建立條件分布充足條件FCDC，統計數據見表1。

根據表1的數據我們可以看出，在已知家庭情況的條件下，性別服從貝努里分布，即[性別|家庭情況]～Bernoulli。

表1 [家庭情況|性別]條件分布概率

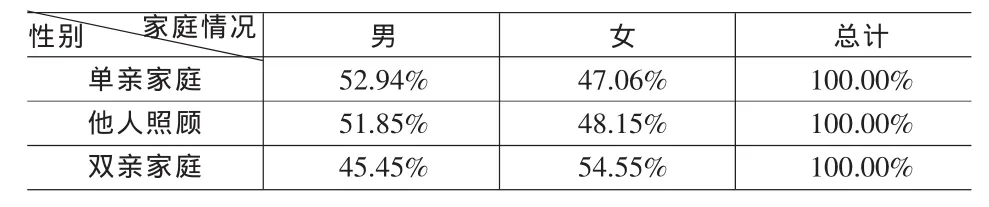
表2 [性別|家庭情況]條件分布概率

表2說明在已知性別的條件下，家庭情況服從三項的離散分布，FCDC條件具備。

（3）仿真數據生成

這里我們使用Excel來實現Gibbs抽樣仿真。首先使用rand（）命令產生隨機數數列。在Excel中，rand（）產生的是0到1之間均勻分布的隨機數，因而所產生的隨機數小于0.6的概率就是0.6。

根據性別產生家庭情況仿真數據所使用的命令語句形式如下

=IF(E2=0,IF(D3＜0.48,1,IF(D3＜0.6667,2,3)),IF(D3＜0.4267,1,IF(D3＜0.6,2,3)))

而根據家庭情況產生性別仿真數據所使用的命令語句為

=IF(F3=1,IF(C3＜0.5294,0,1),(IF(F3=2,IF(C3＜0.5185,0,1), IF(C3＜0.4545,0,1))))

（4）仿真結果評價

仿真數據生成好后，需評價仿真效果以證明抽樣的優越性。統計情況表3所示。

使用Excel的單因素方差分析，顯示結果如表5表6所示。

在表5中，由于F=7.708647＜F0.05(1,4)=7.71，所以接受兩組無差異的原假設，說明在家庭情況屬性中，原數據與仿真數據無顯著性差異。

表3 原數據與仿真數據對比表（家庭情況）

表4 原數據與仿真數據對比表（性別）

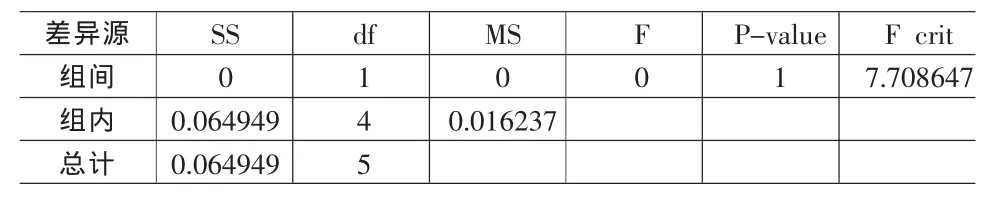
表5 單因素方差分析表顯示結果（家庭情況）

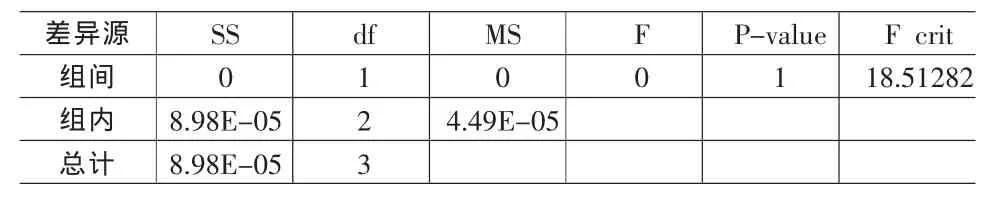
表6 單因素方差分析表顯示結果（性別）

在表6中，由于F=18.51282＜F0.05(1,2)=18.52，所以也接受兩組無差異的原假設，說明在性別屬性中，原數據與仿真數據無顯著性差異。

由此可見，使用Gibbs抽樣對缺失數據進行仿真能獲得較好的效果。

4 結論

本文提出了將Gibbs抽樣仿真應用到缺失值處理中，改善了以往方法不能考慮總體情況的缺陷，在大樣本情況下，能夠很好地將已知的總體分布信息納入到對缺失值的處理當中。

使用Gibbs抽樣進行缺失值處理的優勢在于以下幾點。

首先，Gibbs抽樣仿真能夠較為理想的處理全數據缺失的問題，當有相關關系屬性內數據全部缺失，同樣可以通過Gibbs抽樣對缺失數據進行填充。這就將Gibbs抽樣仿真與傳統的回歸、貝葉斯推導等方法區分開來。

其次，Gibbs抽樣FCDC是根據存在的數據通過統計方法得到的，由于Gibbs抽樣本身所具有的良好性質，保證了所填充數據符合已存在數據的統計特性，從統計意義上而言具有一定的意義。這是Gibbs抽樣仿真與使用人工填寫、全局常量以及各類均值填充缺失值的區別所在。

另外，運用Gibbs抽樣填充缺失數據是十分簡單易行的。只要掌握缺失數據的屬性與其他屬性之間的條件分布，就能夠利用這些分布產生數據。所以當已知的完整數據的數據量足夠大，能夠根據這些完整數據統計得到完整的條件分布，就能夠利用這樣的條件分布產生符合實際需要的數據。

當然Gibbs抽樣作為一種仿真方法，最大的局限性在于仿真的基礎是完全建筑在為隨機數理論和計算機數系上的，偽隨機數理論的算法再好也不是真正隨機的，而計算機數系不但有限而且不完備。因而在使用Gibbs抽樣進行仿真時，需要注意這一點。

[1]Jiawei Han,Micheline Kamber.范明,孟小峰譯.數據挖掘——概念與技術[M].北京:機械工業出版社，2007.

[2]Jerzy W.Grzymala-Busse,Ming Hu.A Comparison of Several Approachesto MissingAttribute Valuesin Data Mining[A]. Rough Sets and Current Trends in Computing[C].Berlin:Heidelberg,2001.

[3]Smith A F M,Roberts G O.Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods[J]. Journal of the Royal statistical Society,1993,55.