應用Crystal Ball實現醫療服務系統排隊模擬和仿真

廈門大學附屬中山醫院信息中心(361004) 嚴 武

排隊是日常生活的一個組成部分。就醫院而言，在患者的就診過程中就產生許多的排隊現象，如候診、取藥、預約檢查等等。許多文獻都說明排隊時間過長會造成診療過程中的一系列問題，陳美珠等〔1〕通過對候診時間與患者血壓、脈搏、狀態焦慮(S-AI)的比較，指出候診時間與患者血壓、脈搏、狀態焦慮(S-AI)呈正相關。邱訪〔2〕和邱靜梅等〔3〕通過對門診患者滿意度的調查均發現，患者對候診時間的滿意度較低。陳蓓等〔4〕在其論文中提到患者的排隊時間過長也是造成無失醫療糾紛的重要原因。因此，通過對排隊問題的研究，找出排隊現象的原因和解決辦法，對合理配置醫療資源、和諧醫患關系等都有十分重要的意義〔5〕。

排隊論作為研究排隊現象的主要工具，起源于A．K．Ering的著名論文《概率與電話通話理論》〔6〕，后被廣泛應用于各個領域，傳統的排隊論模型往往采用靜態的處理辦法，即通過確定的達到時間、服務時間等參數，計算出固定的隊列長度值，等待時間等指標，而無法實現對整個排隊過程的動態模擬，也無法獲得如隊列長度、等待時間的變化情況和分布情況等更多的動態信息。本文以門診患者掛號收費排隊過程為例，應用排隊論結合蒙特卡洛模擬實現對門診候診過程的動態仿真，得到多服務臺情況下的隊列模擬，并對門診排隊現象提出解決相應的建議。

資料與方法

1．資料來源 本文資料來源于廈門市某三甲醫院2009年全年工作日門診患者就診數據，假定隊長為無限，患者按照先到先服務原則進行掛號繳費。患者從等待掛號開始進入排隊系統，直到最后離開。

2．方法 應用sql語句對后臺his數據庫表中的數據進行提取，并將數據轉換為Excel文件，用Excel對數據進行篩選清理等預處理，并利用Excel內置函數建立排隊系統各個參數間的邏輯關系后，用crystal ball 11.1.1.3仿真軟件及VBA編程語言對數據進行

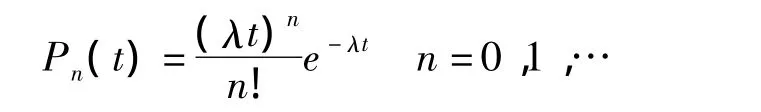
患者到達分布資料經整理后如表1所示，患者的平均到達率λ=26.05(人/分鐘)，病人到達的分布服從λ=26.05的泊松分布，即病人到達間隔時間服從1/λ 的負指數分布(χ2=4.8033，df=6，P=0.5693)。M/M/C排隊系統的動態仿真。

結果與分析

1．數據模型的擬合

當患者是隨機到達時，其間隔時間為負指數分布〔7〕，而患者單位時間的到達分布則應該服從泊松分布。如果在t時段內到達n個患者的概率為Pn(t)，則有:

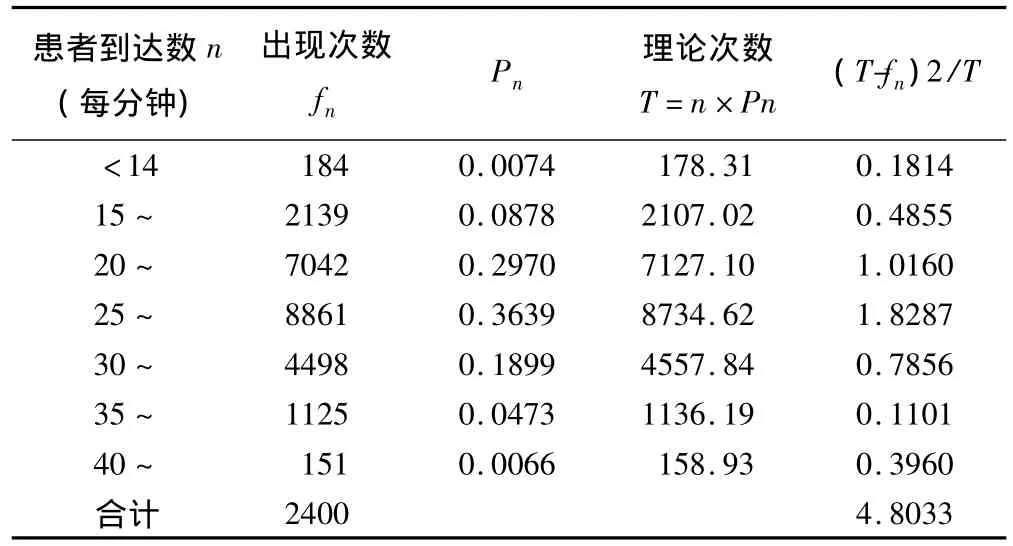
表1 患者到達的分布擬合

表2為窗口工作人員服務時間的指數分布擬合結果，一共有12個開放窗口，每個窗口現場隨機測量20次工作人員的服務時間，假設服務時間服從指數分布，且令服務時間出現在{a，b}(b＞a)時間區間的概率為P(a＜t＜b)，則有:

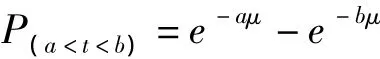
對表2數據的χ2檢驗表明，工作人員的服務時間服從μ=2.5(人/分鐘)的指數分布，結果有統計學意義(χ2=10．1109，df=11，P=0．5204)。

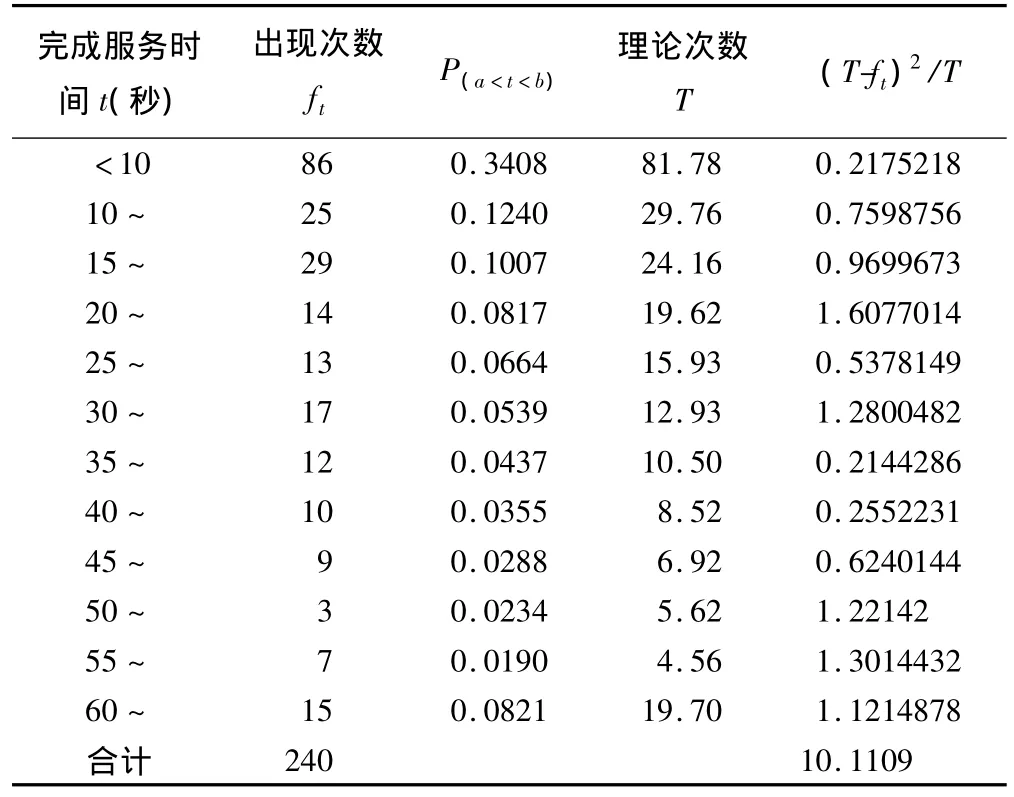
表2 服務時間分布的擬合

2．M/M/C排隊系統的的模擬仿真及結果分析Crystal Ball是由美國Decisioneering公司開發的一種運用模擬方法對不確定性(有時也指風險)進行定量分析的軟件，后被Oracle公司收購，其應用領域很廣泛，使用用戶也非常多，據悉在世界500強中有85%的公司，以及美國前50所最佳MBA商學院有40所都在使用它作為解決商業課題和教研的工具〔8〕。國內也有相關的應用和研究，主要集中在商業應用及企業的生產質量控制等領域，在國內醫療衛生行業中的應用卻鮮有報道。Crystal Ball作為Excel的一種加載宏運行，在與Excel無縫集成的同時，可以結合Excel的特點，并利用自身模擬的優勢，實現對不確定性的定量分析，其基本應用步驟為〔9〕:(1)模型建立。這一步主要是在Excel表中進行，一般根據實際問題情況輸入有關數據、公式和設定有關變量，如需要模擬的變量的概率分布(軟件中內置的概率分布多達20種，同時也可自己定義分布)、需預測的數據單元;如果是一個決策問題，還需要定義決策變量。(2)模型模擬。當數據輸入、模型建立完畢后，點擊菜單Run中的Start Simulation(安裝啟動Crystal Ball后，Excel主菜單中增加Define，Run，Analyze 3個菜單)，便進入模擬運行階段，由軟件自身完成整個模擬過程。(3)結果分析。模擬運行結束后，軟件會自動生成有關分析結果，如預測值可以圖表形式直觀確定對應的概率、預測值的敏感性因素影響分析和運行過程中數據的抽取保存等。

根據對數據的擬合結果，擬采用M/M/C排隊模型進行模型仿真，在Excel數據表中分別輸入模擬需要的各個參數值，以及需要求解和預測的變量的計算公式。關于M/M/C排隊系統的原理、應用條件和計算方法許多教材和論著均有專門的闡述，本文不再列出詳細的計算公式。運行crystal ball軟件，在單元格中定義λ及μ的分布類型，定義預測變量為隊列中的等待人數Lq以及患者在隊列中的等待時間Wq，將模擬次數設為5000次，進行蒙特卡洛模擬仿真〔10〕，結果如圖1及圖2所示。可以看出，而經過5000次 模擬計算出的Lq和Wq的均值分別為3．86人和0．13分鐘，排隊論公式計算的結果3．5912人和0．1379分鐘，差別并不大，如果能適當增加模擬次數，兩者的值還會更加接近。則在圖1中可以看出，超過3人以上的概率為85．15%，說明隊列中排隊現象出現的概率還是很大的。另外，結合5000次模擬的Wq頻數分布來看，雖然該系統有排隊現象，但患者在隊列中的等待時間并不長，基本上可以在較短的時間內得到服務。

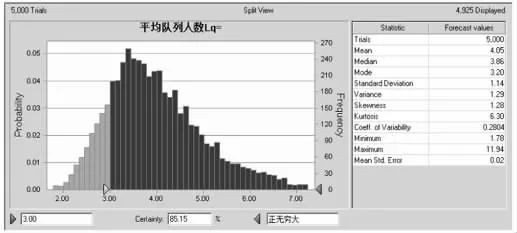
圖1 crystal ball中輸出的隊列等待患者數Lq的模擬結果

圖2 crystal ball中輸出的患者在隊列中等待時間Wq的模擬結果

我們還可以利用crystal ball中cb．exponential()函數產生隨機的指數分布，從而對患者到達的間隔時間和窗口服務時間進行仿真。通過仿真，我們發現，排隊的高峰時刻和最大排隊人數均出現在9:30～10:00的區間段，這也與我院的實際情況比較吻合。

討 論

1．到醫院就診排隊是一種常見現象，由于患者到達和醫療服務時間的隨機性，患者來源數量在理論是無限的，而醫療資源是有限的，當醫療服務的現實需求超過提供該項服務的現有能力時，排隊就會發生，因此排隊現象是不可避免的。如果患者的等待時間和排隊等待的隊列長度過長，超過了實際可能承受的限度而遠遠無法滿足患者的需要時，必將造成患者的流失，同時可能影響患者的診斷和救治，使急需診治的患者無法得到及時的醫療服務，甚至危及患者的生命，影響醫療質量。

2．傳統的模擬和預測建模工具往往需要使用者較為專業的理論知識和建模能力，Crystal ball作為一種模擬和預測工具，在應用廣泛的Excel電子表格上加載運行，相比其他使用設計復雜的程序和煩瑣的計算機編程語言，如 Matlab 6．5、CISMAN、Visual Basic，用Crystal ball建模具有直觀簡便、操作性更強、適用性更廣等優點，降低了建模的難度和操作性，輸出的結果清晰易懂，并且可以轉換成excel格式文件進行編輯，實現了和OFFICE組件的無縫鏈接〔11〕。

3．本文以門診患者就診流程為例，應用 Crystal ball結合排隊論進行M/M/C隊列的模擬仿真，在傳統排隊論的基礎上，實現了對排隊系統的動態分析，并對仿真結果進行分析和評價，為提高醫院的醫療服務效率和優化醫療資源提供了科學參考依據。

1．陳美珠，劉桂卿，馮惠芳，等．候診時間與狀態焦慮的相關性研究．中國行為醫學科學，2005，14(9):825-826．

2．邱訪．影響我院門診患者滿意度的因素分析及解決方案．華西醫學，2009，24(6):1502-1504．

3．邱靜梅，王健．山東某縣綜合性醫院門診患者滿意度分析．中國社會醫學雜志，2009，26(5):17-319．

4．陳蓓，許翔，江一峰．無過失醫療糾紛的現狀分析．中國衛生事業管理，2009，250(4):243-244．

5．周文正，尹平，馬玉全，等．排隊論模型M/D/c在醫療服務系統中的應用．中國衛生統計，2009，26(6):608-610．

6．Cliff TR．電子表格建模與決策分析．第4版．杜學孔，崔鑫生譯．北京:電子工業出版社，2006，530-531．

7．Frederick SH，Mark SH．數據、模型與決策．第2版．任建標譯．北京:中國財政經濟出版社，2004，593-596．

8．楊琴，胡輝．基于Crystal Ball的項目管理建模分析．中國管理信息化，2007，10(12):27-29．

9．http://download．oracle．com/docs/cd/E12825_01/epm．111/cb_user/frameset．htm?index．html．

10．劉清志，許學娜．Excel在蒙特卡羅模擬分析中的應用．中國管理信息化，2008，11(7):44-47．

11．文偉，葉春明，劉曉樂．基于Excel的蒙特卡羅模擬在銀行排隊業務中的應用．中國管理信息化，2008，11(6):81-84．