EGO算法的翼型氣動(dòng)外形優(yōu)化設(shè)計(jì)

侯成義

(西北工業(yè)大學(xué)國(guó)防科技研究院，710072西安，peggy.cao@163.com)

遺傳算法、粒子群算法等隨機(jī)優(yōu)化算法同基于梯度的優(yōu)化算法相比具有很強(qiáng)的全局性和魯棒性，然而這些隨機(jī)優(yōu)化算法進(jìn)行需要用CFD、FEM分析等耗時(shí)的目標(biāo)值評(píng)估的工程優(yōu)化時(shí)，存在著計(jì)算量大的問題，嚴(yán)重制約了在工程中的應(yīng)用.用代理模型代替費(fèi)時(shí)的精確模型計(jì)算進(jìn)行優(yōu)化的方法得到了發(fā)展［1-2］，常用的代理模型有多項(xiàng)式響應(yīng)面模型、人工神經(jīng)網(wǎng)絡(luò)模型、Kriging模型等.首先由一定數(shù)量的樣本構(gòu)造代理模型，用優(yōu)化算法搜索代理模型的最優(yōu)解并進(jìn)行精確模型校驗(yàn)，進(jìn)而更新校驗(yàn)點(diǎn)到代理模型直至滿足收斂要求.由于代理模型的計(jì)算量比精確模型小得多，該方法可大幅度提高優(yōu)化效率，但是其優(yōu)化精度嚴(yán)重依賴于代理模型預(yù)測(cè)的能力，容易陷入局部最優(yōu)［3］.M.Schonlau［4］提出的EGO(Efficient Global Optimization)算法在選取校驗(yàn)點(diǎn)時(shí)綜合考慮了代理模型的預(yù)測(cè)值和預(yù)測(cè)精度，有效避免了陷入局部最優(yōu)的風(fēng)險(xiǎn)，該方法在工程優(yōu)化中得到了應(yīng)用［5-6］.

本文采用拉丁超立方實(shí)驗(yàn)設(shè)計(jì)方法產(chǎn)生樣本點(diǎn)，用EI(Expected Improvement)最優(yōu)策略綜合評(píng)價(jià)由Kriging代理模型獲取的預(yù)測(cè)適應(yīng)值及預(yù)測(cè)精度，并結(jié)合響應(yīng)最優(yōu)策略，用粒子群算法搜索最優(yōu)校驗(yàn)點(diǎn)，結(jié)合Hicks-Henne型函數(shù)翼型參數(shù)化方法與雷諾平均N-S方程流場(chǎng)求解器進(jìn)行了翼型優(yōu)化設(shè)計(jì).

1 優(yōu)化系統(tǒng)

1.1 試驗(yàn)設(shè)計(jì)方法

選取合理分布的樣本點(diǎn)對(duì)構(gòu)造代理模型具有重要的影響，一般要求有限的樣本應(yīng)該盡可能全面的反映設(shè)計(jì)空間的特性.常用的實(shí)驗(yàn)設(shè)計(jì)方法有全析因設(shè)計(jì)、正交設(shè)計(jì)、均勻設(shè)計(jì)等，本文采用了拉丁超立方設(shè)計(jì)方法產(chǎn)生樣本點(diǎn).

1.2 粒子群優(yōu)化算法

粒子群優(yōu)化算法(Particle Swarm Optimization)［7］是一種模擬鳥群覓食行為的群體智能算法，該算法實(shí)現(xiàn)簡(jiǎn)單，參數(shù)設(shè)置方便，收斂速度快，能有效解決復(fù)雜優(yōu)化問題.該算法以“粒子”作為個(gè)體，按照設(shè)定的規(guī)則進(jìn)行群體的協(xié)作從而進(jìn)行有效的搜索.首先隨機(jī)初始化粒子種群位置和初速度，每個(gè)粒子通過跟蹤自身所找的個(gè)體最優(yōu)粒子pbest以及整個(gè)種群找到的全局最優(yōu)粒子gbest，在粒子當(dāng)前速度、pbest和gbest的位置的共同引導(dǎo)下，粒子在下一個(gè)時(shí)刻將飛行到新的位置.粒子的速度和位置更新公式分別為

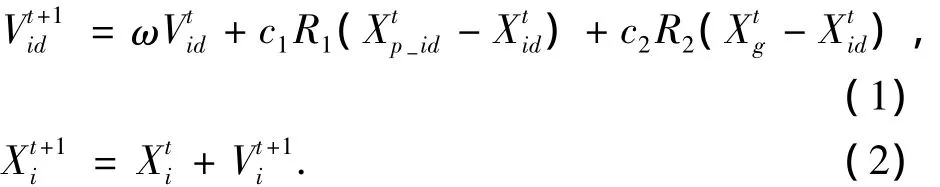
式中:d=1，2，…，n(n為搜索空間維數(shù));i=1，2，…，m(m為種群規(guī)模);t為當(dāng)前進(jìn)化代數(shù);分別為對(duì)應(yīng)粒子的歷史最優(yōu)位置和全局最優(yōu)位置;c1，c2分別為學(xué)習(xí)因子;R1，R2分別為(0，1)的隨機(jī)數(shù);ω為慣性權(quán)重因子，慣性權(quán)重因子決定了粒子先前速度對(duì)當(dāng)前速度的影響程度.Shi Y采用隨迭代進(jìn)行慣性權(quán)重因子減小的方法，在優(yōu)化初期提高全局搜索能力，而在后期加速收斂.

1.3 Kriging代理模型

Kriging代理模型［8］起源于地理空間統(tǒng)計(jì)學(xué)，是一種估計(jì)方差最小的無偏估計(jì)模型，通過相關(guān)函數(shù)的作用，具有局部估計(jì)的特點(diǎn)，它可以較好的預(yù)估未知點(diǎn)處函數(shù)值的分布情況.Kriging模型假設(shè)目標(biāo)函數(shù)值與設(shè)計(jì)變量之間的真實(shí)關(guān)系可以寫為

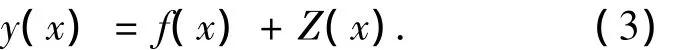
式中:f(x)為回歸模型，是對(duì)設(shè)計(jì)空間的全局近似，為確定性部分，可以一個(gè)常數(shù)β表示;Z(x)為均值為0，方差為σ2的統(tǒng)計(jì)過程，表示對(duì)全局近似的背離，2個(gè)插值點(diǎn)的協(xié)方差為

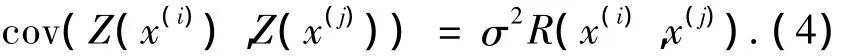
式中R為點(diǎn)x(i)和x(j)的相關(guān)函數(shù)，可用高斯函數(shù)表示為

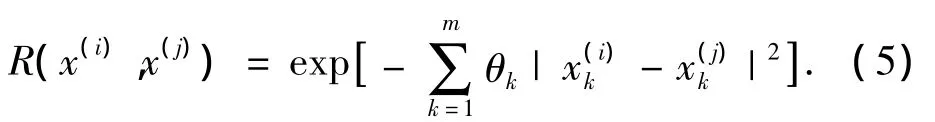
未知點(diǎn)x0處的預(yù)測(cè)值^y(x0)和方差估計(jì)值^σ通過下列形式給出:

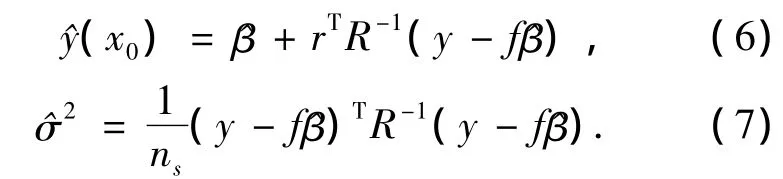
可以通過極大似然估計(jì)確定相關(guān)參數(shù)θk為

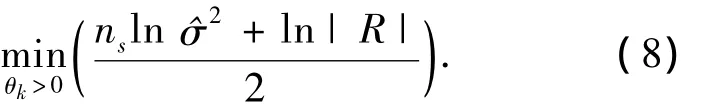
1.4 EGO算法

選擇代理模型預(yù)測(cè)值的最優(yōu)點(diǎn)作為校驗(yàn)點(diǎn)的方法稱為響應(yīng)最優(yōu)策略.但是代理模型的預(yù)測(cè)精度總是有限的，如果代理模型在真實(shí)的最優(yōu)解處預(yù)測(cè)精度較差，就有可能在選擇校驗(yàn)點(diǎn)時(shí)總是無法搜索到該區(qū)域，使得優(yōu)化陷入局部最優(yōu).因此在選擇校驗(yàn)點(diǎn)時(shí)有必要綜合考慮Kriging模型獲取的預(yù)測(cè)適應(yīng)值及預(yù)測(cè)精度.本文采用了EI(Expected Improvement)方法，根據(jù)下式確定個(gè)體的EI值，EI值越大說明該個(gè)體越需要校正.

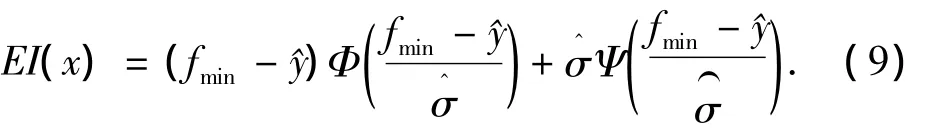
式中:fmin為樣本點(diǎn)中最小適應(yīng)值;^y為預(yù)測(cè)適應(yīng)值為預(yù)測(cè)標(biāo)準(zhǔn)差;Φ，Ψ分別為標(biāo)準(zhǔn)正態(tài)分布和標(biāo)準(zhǔn)正態(tài)分布密度函數(shù).當(dāng)個(gè)體預(yù)測(cè)值越小，預(yù)測(cè)標(biāo)準(zhǔn)差越大，則個(gè)體的EI值越大，個(gè)體越需要校正.

1.5 優(yōu)化流程

本文在選擇校驗(yàn)點(diǎn)時(shí)，一部分校驗(yàn)點(diǎn)用響應(yīng)最優(yōu)策略選擇，另一部分采用EI最優(yōu)策略，2種方法交替進(jìn)行.優(yōu)化流程為:

1)由拉丁超立方設(shè)計(jì)方法在設(shè)計(jì)空間內(nèi)生成一定數(shù)量的樣本.

2)由樣本點(diǎn)構(gòu)建Kriging代理模型.

3)確定是采用響應(yīng)最優(yōu)策略還是EI最優(yōu)策略，基于粒子群算法優(yōu)化選擇最優(yōu)響應(yīng)或最優(yōu)EI校驗(yàn)點(diǎn).

4)判斷是否滿足收斂條件，如果滿足則退出，不滿足則執(zhí)行步驟5).

5)將校驗(yàn)點(diǎn)加入樣本，執(zhí)行步驟2).

2 翼型氣動(dòng)優(yōu)化設(shè)計(jì)

翼型參數(shù)化方法采用的是Hicks-Henne型函數(shù)法［9］，新翼型由基本翼型的上表面或下表面加擾動(dòng)構(gòu)成，表達(dá)為

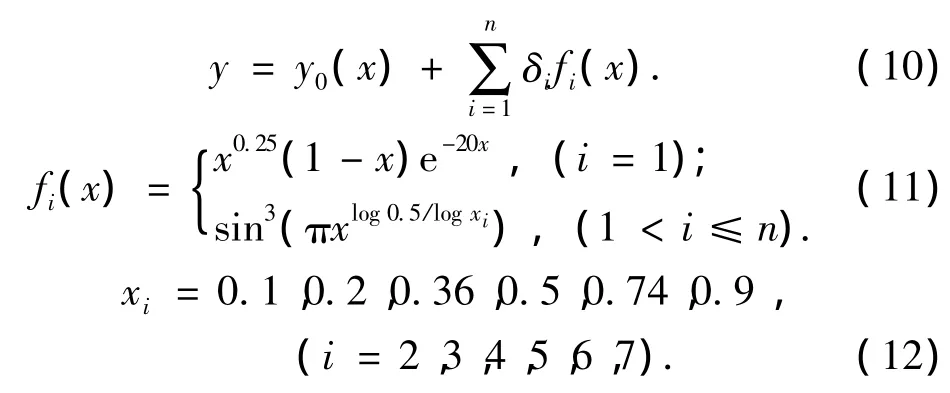
式中n為控制上表面或下表面變量的個(gè)數(shù)，本文選取n為7，即共計(jì)14個(gè)設(shè)計(jì)變量.

本文以RAE2822翼型為初始翼型進(jìn)行翼型氣動(dòng)優(yōu)化設(shè)計(jì)研究.采用雷諾平均N-S方程求解繞翼型流場(chǎng)，湍流模型為k-ω SST模型.設(shè)計(jì)狀態(tài)為巡航馬赫數(shù)0.73，雷諾數(shù)6.5E6，設(shè)計(jì)升力系數(shù)0.74，約束條件為最大相對(duì)厚度不減，低頭力矩特性不差于初始翼型，優(yōu)化目標(biāo)為降低阻力系數(shù).

由拉丁超立方設(shè)計(jì)方法產(chǎn)生120個(gè)翼型作為代理模型初始樣本點(diǎn)，校驗(yàn)次數(shù)為240，EI最優(yōu)策略進(jìn)行2次后響應(yīng)最優(yōu)策略進(jìn)行1次，如此交替進(jìn)行，即分別進(jìn)行160次和80次，PSO的種群規(guī)模為30，迭代步數(shù)為60.為了比較本文優(yōu)化方法，還采用響應(yīng)最優(yōu)法和粒子群算法進(jìn)行翼型優(yōu)化，其中響應(yīng)最優(yōu)法初始樣本數(shù)為120，校驗(yàn)次數(shù)為240，而粒子群算法種群規(guī)模為30，迭代步數(shù)為40，設(shè)計(jì)結(jié)果如表1所示.單純的響應(yīng)最優(yōu)法優(yōu)化陷入局部最優(yōu)，其他2種方法得到了相似的優(yōu)化結(jié)果，阻力降低了22.4%，粒子群算法用了1 200次流場(chǎng)計(jì)算，而本文方法僅用360次.圖1和圖2分別為本文方法優(yōu)化前后翼型形狀和壓力分布，與初始翼型相比，設(shè)計(jì)翼型翼型完全消除了激波，阻力系數(shù)降低了0.003 4，而翼型最大相對(duì)厚度沒有降低.設(shè)計(jì)翼型整體彎度降低，而通過增加后加載來保持升力系數(shù).同時(shí)設(shè)計(jì)翼型增加了前加載和頭部上表面吸力峰值，一方面增加了翼型升力，另一方面抵消了后加載所附加的低頭力矩，使設(shè)計(jì)翼型保持著良好的低頭力矩特性.

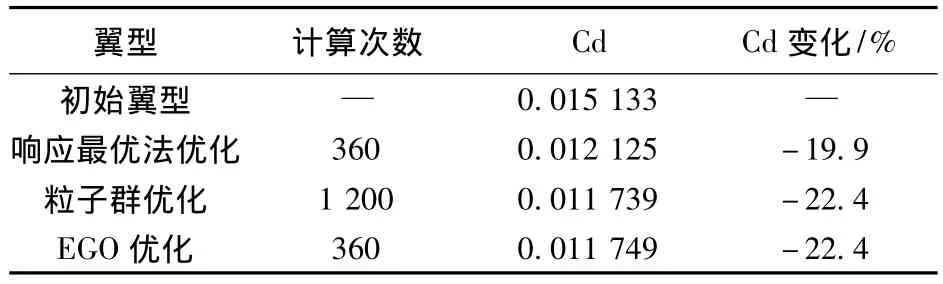
表1 不同優(yōu)化方法計(jì)算次數(shù)及優(yōu)化結(jié)果對(duì)比

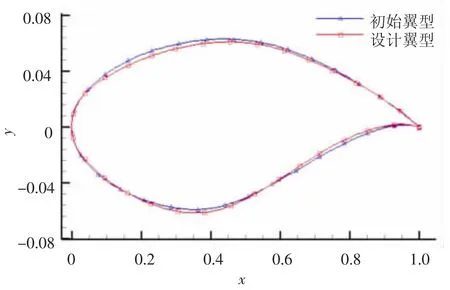
圖1 設(shè)計(jì)翼型與初始翼型形狀

雖然構(gòu)造Kriging模型以及預(yù)測(cè)氣動(dòng)力需要耗費(fèi)一定時(shí)間，但是與調(diào)用氣動(dòng)力計(jì)算的耗時(shí)相比要小得多，上文算例優(yōu)化耗時(shí)約比粒子群算法減少68%.

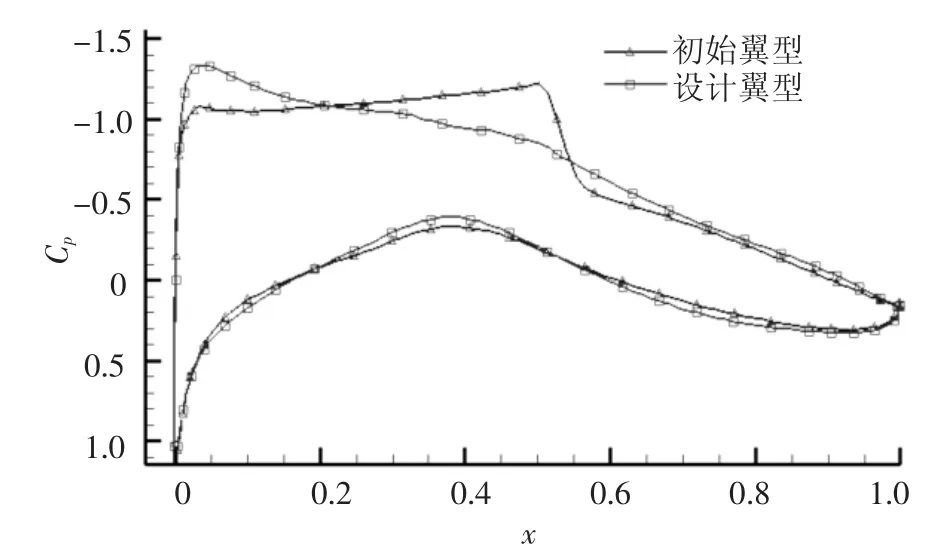
圖2 設(shè)計(jì)翼型與初始翼型壓力分布

3 結(jié)論

1)本文構(gòu)建了將Kriging代理模型和粒子群算法相結(jié)合的高效優(yōu)化系統(tǒng)，采用粒子群算法搜索由EI最優(yōu)策略和響應(yīng)最優(yōu)策略交替選擇的最優(yōu)校驗(yàn)點(diǎn)，前者綜合考慮代理模型的預(yù)測(cè)值及預(yù)測(cè)精度，可以有效避免陷入局部最優(yōu)，后者可以促使快速收斂.

2)翼型優(yōu)化設(shè)計(jì)算例表明本文方法克服了響應(yīng)最優(yōu)法容易陷入局部最優(yōu)的缺點(diǎn)，保證優(yōu)化精度，同時(shí)又有效地減少了計(jì)算量，大大提高了翼型氣動(dòng)優(yōu)化設(shè)計(jì)的工程實(shí)用性.

［1］DUVIGNEAU R，VISONNEAU M.Hybrid genetic algorithms and neural networks for fast CFD-based design［R］.Atlanta:AIAA 2002-5465，2002.

［2］RAJAGOPAL S，GANGULI R.Multidisciplinary design optimization of an UAV wing using kriging based multi-objective genetic algorithm［R］.AIAA 2009-2219，2009.

［3］JONES D L.A taxonomy of global optimization methods based on response surfaces［J］.Journal of Global Optimization，2001，21(4):345-383.

［4］SCHONLAU M.Computer experiments and global optimization［D］.Ontario Canada:Waterloo，1997.

［5］王紅濤，竺曉程，杜朝輝.基于Kriging代理模型的改進(jìn)EGO算法研究［J］.工程設(shè)計(jì)學(xué)報(bào)，2009，16(4): 266-270.

［6］蘇偉，高正紅，夏露.一種代理遺傳算法及其在氣動(dòng)優(yōu)化設(shè)計(jì)中的應(yīng)用［J］.西北工業(yè)大學(xué)學(xué)報(bào)，2008，26(3):303-307.

［7］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Washington，DC:IEEE Service Center，1995:1942-1948.

［8］CRESSIE N A C.Statistics for spatial data［M］.New York:John Wiley＆Sons，1993.

［9］HICKS R M，HENNE P A.Wing design by numerical optimization［J］.Journal of Aircraft，1978，15(7): 407-413.