一種適用于功能電路的自組織神經網絡模型構建

巨政權,張海川,滿夢華

(1.軍械工程學院 靜電與電磁防護研究所,石家莊 050003;2.解放軍63961部隊 25分隊,北京 100012)

1 引 言

復雜電磁環境對電子系統具有很強的干擾作用。然而,生物體的神經系統卻表現出非凡的適應性與魯棒性[1]。特別是在過量電刺激的作用下,生物體內的電磁信號傳遞卻不受影響,個體的生理活動仍然能夠正常運行。若將生物體神經系統的這種特性引入到電子電路實踐中,可用于提高電子系統的抗電磁干擾能力以及復雜電磁環境下電子裝備的可靠性。傳統的人工神經網絡(Artificial Neural Network,ANN)在自適應學習、信息處理方面具有較好的魯棒性和容錯能力[2-5],但在構建具有生物神經系統特性的電子系統時,其具有以下局限性:一是傳統的神經網絡模型與電子電路之間沒有較好的對等映射關系;二是傳統神經網絡模型的權值變換硬件實現可行性較差。

為解決上述問題,本文借鑒傳統人工神經網絡設計架構,提出了一種具有較強自組織特性的神經網絡模型。該模型與電子電路具有較好的對等映射關系。后續實驗也證明了應用該模型進行權值變換硬件實現的可行性。而且,基于該模型,可較為方便地實現各種功能電路,并使得實現的電路整體具有一定的自組織特性,為后續實現具有自修復、自適應特性的電路提供了理論和技術基礎支撐。

2 自組織神經網絡模型的構建

2.1 神經元模型[6-8]

神經元模型由加權變換、激勵變換兩部分組成,如圖1所示。G(·)和 f(·)分別表示加權變換和激勵變換函數。向量P=(p1,p2,…,pm)為神經元輸入向量,A=(a1,a2,…,at)為激勵向量,t為激勵參數量。A=G(P)=PW,其中 W(W為m×t矩陣,每列均為坐標向量)為加權矩陣,描述了神經元對輸入向量的遴選情況。根據神經元在不同狀態下激勵特性不盡相同的特點,激勵函數f(·)在此具有可變性。b為神經元的激勵輸出,c為神經元狀態函數,用于描述神經元的狀態。當c=1時,神經元正常;c=0時,神經元失效,輸出值恒為0。

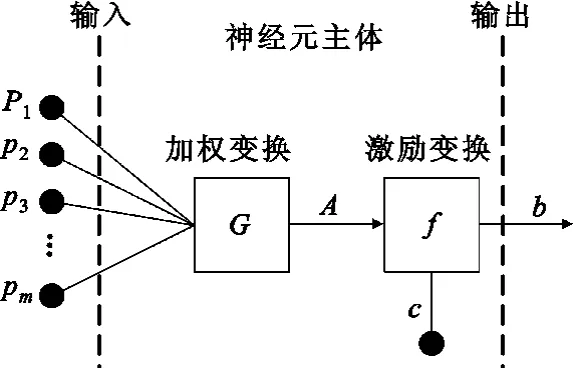
圖1 神經元模型Fig.1 The neuron model

該模型的數學形式可表示為

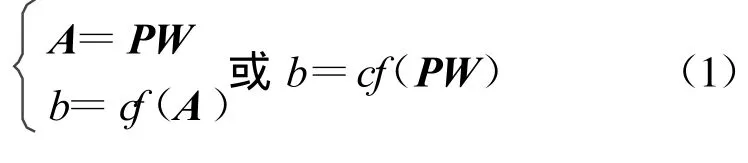
提出的自組織神經網絡神經元與傳統神經網絡神經元的主要區別有兩點:第一,權值只有0和1兩種情況,即只有斷開、連接兩種狀態;第二,激勵函數是一個由多個具體函數組成的函數群,可根據具體狀態激活其中某一函數。

2.2 神經網絡模型

在自組織神經網絡模型中,借鑒分層前饋方式人工神經網絡模型[2]進行網絡拓撲構建,一個由m×n個神經元組成的神經網絡如圖2所示。

圖2 自組織神經網絡模型Fig.2 The self-organizing neural networks model

由圖2可知,自組織神經系統對信號進行分層、并行傳遞,每層輸出包含傳遞信息的所有特征。神經元無需知道傳遞信息所有情況,只按照某種既定規律進行信號轉化傳輸。神經網絡中權值矩陣 W確定了神經網絡的邏輯結構,若第(i,j)個神經元對應的參數為Wi,j、fi,j和ci,j,則整個神經網絡可由權值矩陣W、功能矩陣F、狀態矩陣C唯一確定:

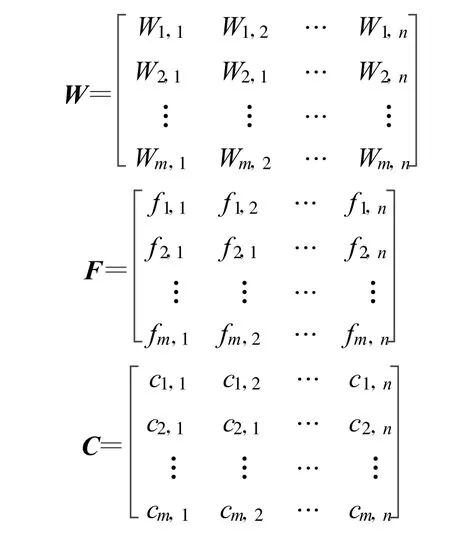
若第 k層的輸入向量Pk=(p1,k,p2,k,…,pm,k),輸出向量Bk=(b1,k,b2,k,…,bm,k),則由公式(1)可知,bi,k=ci,kfi,k(PkWi,k),其中 i=1,2,…m。從網絡拓撲可知,Pk+1=Bk,k=1,2,…,n,且有P1=(p1,1,p2,1,…,pm,1)為已知初始輸入向量,所以網絡中的信號流可描述為

式中,i=1,2,…,m;k=1,2,…,n。

2.3 信號在神經網絡中的傳遞過程

在自組織神經網絡模型中,信號在自組織神經網絡中分層并行傳遞,每層對信號的傳遞是一種解釋傳遞,即將上層傳遞的信號“解釋”為下層所能理解的信號。系統輸出與輸入信號不盡相同,但其“解釋”對應同一組信息特性,即具有相同物理意義。

神經網絡所傳輸的信號來自識別系統輸入信號X=(x1,x2,…,xt)。要對識別信息無失真傳輸,則必須有t≤m,即所傳輸信號向量的長度不能大于神經網絡所能傳輸向量的最大長度。若符合無失真傳輸要求,可將X直接賦值給P1,即P1=X。

網絡輸出的生物意義是指將神經網絡中傳輸的有效信號傳輸給大腦識別的過程。有效輸出信號Y=(y1,y2,…,yk)是指可被大腦接收的信號,是第n層神經元輸出的一個真子集,即k≤m,識別所需信號向量長度不能大于網絡所能傳輸向量的最大長度。網絡輸出Y=BnV,V為輸出權值矩陣(每列均為坐標向量的m×k矩陣),其物理意義為在第n層神經網絡的輸出中有序篩選出有用信號。結合公式(2),自組織神經網絡模型的信號傳遞過程可表示為

式中,i=1,2,…,m;k=1,2,…,n。

3 功能電路到神經網絡映射及其自組織實現

3.1 功能電路到神經網絡的映射

一般來說,功能電路由多個基本電路單元(或器件)按照特定的拓撲結構連接而成。若將電路輸入(輸出)映射為神經網絡輸入(輸出),基本電路單元(器件)映射為神經元,電路連接映射為權值連接,電路拓撲映射為神經網絡拓撲,則電子電路與神經網絡具有較好的對等映射關系,如圖3所示。

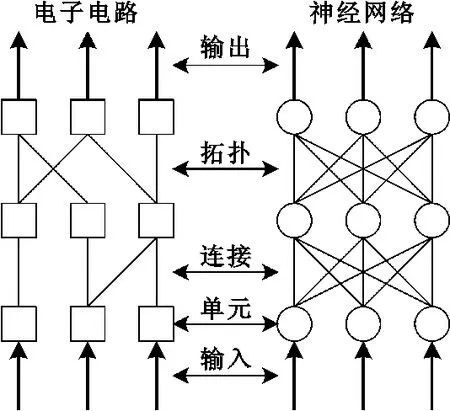
圖3 電子電路與神經網絡的對等映射Fig.3 The mapping between the electronic circuit and the neural networks

圖4給出了由電路功能到神經網絡的映射關系。易見,在映射過程中,同一種電路功能可由多種電路拓撲實現。同時,同一種電路拓撲可以對應多種空間上的物理實現,即基于同功能的電路在同一神經網絡上可通過權值矩陣和函數矩陣變換,以多種物理結構加以實現,這便是本文中構建神經網絡系統進行自組織,以及后續研究利用其實現自修復、自適應電路的物理基礎。

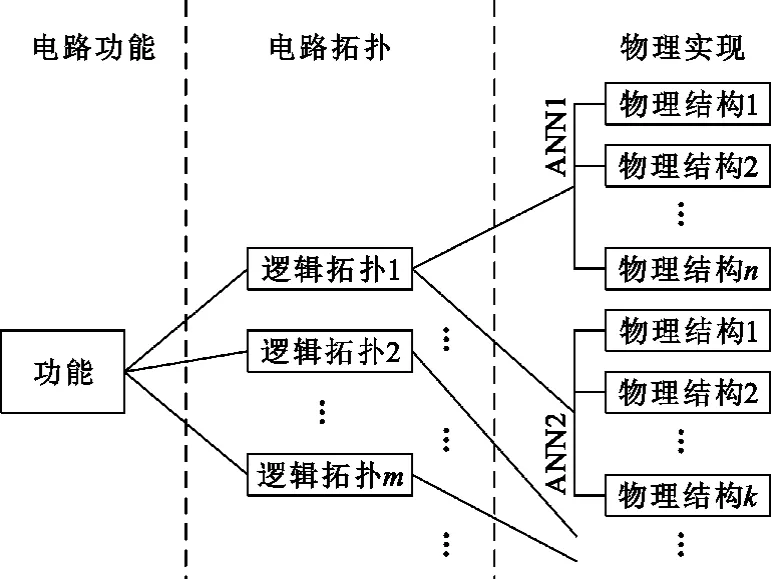
圖4 電路功能到神經網絡的映射Fig.4 The mapping form function to the neural networks

3.2 自組織方法描述

在神經網絡發生“異常”時,其自組織特性是保證系統邏輯拓撲不變和功能正常實現的基礎。此時,神經網絡系統常需要重組,重組步驟為:首先對每層內神經元隨機生成一個邏輯序號形成一個層邏輯序列,然后再根據每層中邏輯序列與物理序列的情況完成權值矩陣與函數矩陣的變換,即實現系統自組織。

為便于描述,定義 Wk=(W1,k,W2,k,…,Wm,k)、Fk=(f1,k,f2,k,…,fm,k)分別為第 k層所對應的權值矩陣向量和功能函數向量,V=(V1,V2,…,Vm)為輸出權值矩陣向量,Vi為輸出權值矩陣V的第i個行向量,則系統自組織方法可描述如下:

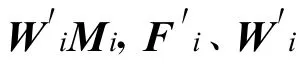
神經網絡整體重組可分解為若干單層重組事件并依次進行處理,其變換算法可描述為

需要說明的是,各層隨機產生的神經元邏輯序列,相當于對其物理序列所構建的行向量進行多次列變換形成,所以變換矩陣Mi必為某一單位矩陣經過相應的列變換而來。由于層邏輯序列在整個自組織過程中僅起到橋梁作用,可以考慮直接對單位矩陣E進行多次隨機行(列)變換來確定 Mi,即 Mi=rand(E)。從而,神經網絡的自組織過程又可描述為

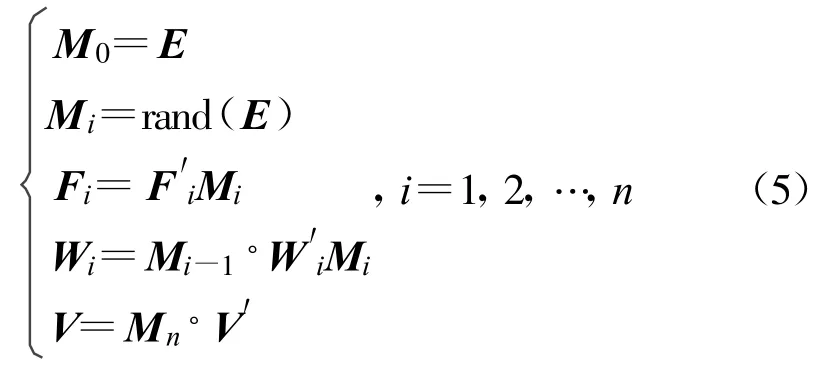
4 實例分析

下面以2×2乘法器為功能電路,取6×6的網絡結構,本文中提出的自組織神經網絡模型對電子電路的承載和自組織方法可描述如下。

4.1 神經元的確定

根據2×2乘法器特點,可設計神經元為2輸入、1輸出的單元,如圖5所示。

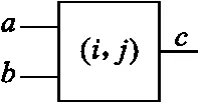
圖5 神經元的設計Fig.5 The neuron designed

圖5中,i、j表示此神經元為第j層第i個神經元;a、b表示所對應的輸入連接第j-1層第a、b神經元輸出;c為神經元功能函數標號,其中,1為與非,2為或,3為異或,4為與。

4.2 功能電路的實現[9,10]

借助遺傳算法,可求解2×2乘法器承載于6×6神經網絡模型時的一種具體物理實現,如圖6所示,其對應的電路拓撲如圖7所示。

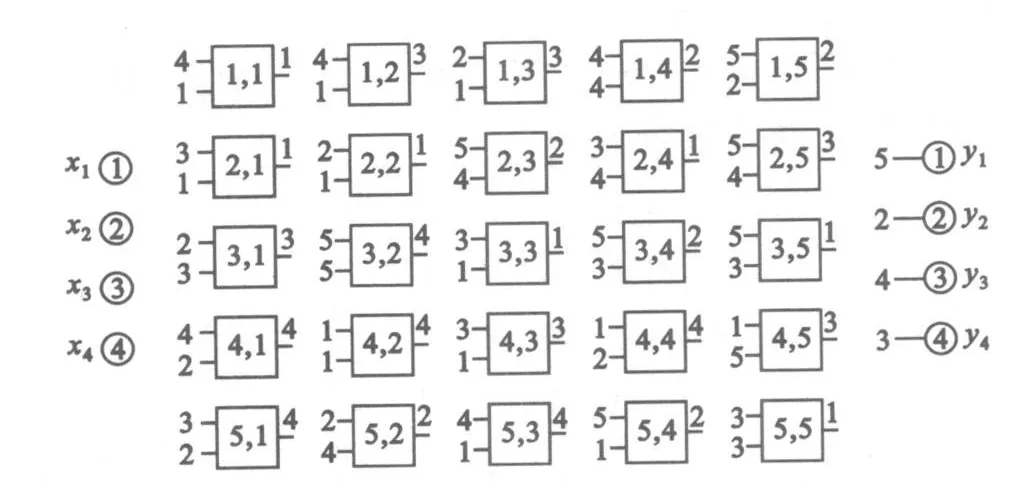
圖6 2×2乘法器的物理實現Fig.6 Physical implementation of the 2×2 multiplier

圖7 2×2乘法器的電路拓撲Fig.7 The topplogy of the 2×2 multiplier

規定由坐標向量組成的m×n維矩陣可用其各列向量對應的坐標數表示為[(t1,t2,…,tn)],ti表示其第i個列坐標向量的第ti元素為1,則構建的神經網絡參數可描述為

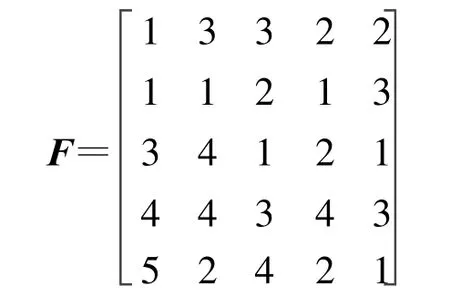
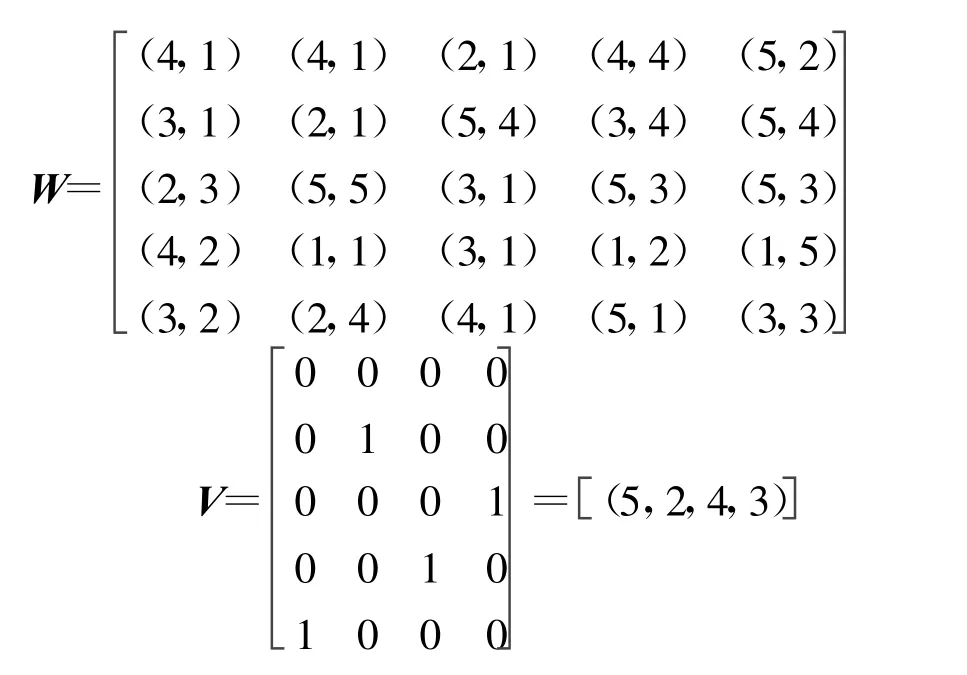
4.3 自組織方法的描述

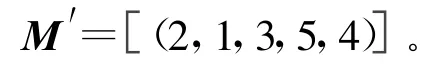
(1)單層重組,M1=M′,M2=M3=M4=M5=E時,神經網絡參數為

(2)相鄰兩個層重組,M1=E,M2=M3=M′,M4=M5=E,神經網絡參數為

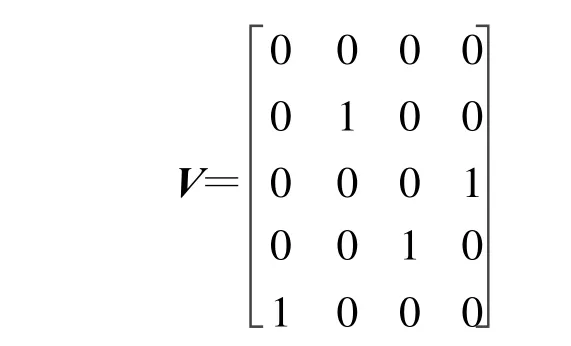
(3)所有層重組,M1=M2=M3=M4=M5=M′,神經網絡參數為

通過對5種情況下的網絡結構進行簡化,消除冗余神經元,可以發現:經過不同重組方式后,神經網絡所對應的電路邏輯拓撲保持一致,電路功能唯一。因此,可以得出結論:所設計的自組織神經網絡模型對功能電路具有較好的承載性和自組織特性。

5 結束語

自組織神經網絡模型的構建是將生物自組織特性引入電子電路設計實踐的一種嘗試,其自組織過程實質就是在電路功能不變情況下,基于網絡拓撲進行不同物理實現的相互轉換。當網絡中某個神經元的某個功能受損或者神經元損毀,可通過神經網絡的自組織特性,利用同層中其它神經元的冗余功能或者層中的冗余神經元進行替代,從而確保電路邏輯拓撲的穩定性及功能的完備性。在此基礎上可開展后續研究,進一步實現電子系統的自修復和自適應特性,提高復雜電磁環境下電子裝備的可靠性。

[1] 劉尚合,原亮,褚杰.電磁仿生學——電磁防護研究的新領域[J].自然雜志,2009,31(1):1-7.LIU Shang-he,YU AN Liang,CHU Jie.Electromagnetic Bionics-A New Study Field of Electromagnetic Protection[J].Chinese Journal of Nature,2009,31(1):1-7.(in Chinese)

[2] Martin T Hagan,Howard B Demuth,Mark H Beale.神經網絡設計[M].戴葵,宋輝,譚明峰,等,譯.北京:機械工業出版社,2002.Martin T Hagan,Howard B Demuth,Mark H Beale.Neural Network Design[M].Translated by DAI Kui,SONG Hui,TAN Ming-feng,et al.Beijing:China Machine Press,2002.(in Chinese)

[3] 何新貴,許少華.過程神經元網絡[M].北京:科學出版社,2007.HE Xin-gui,XU Shao-hua.Process Neural Networks[M].Beijing:Science Press,2007.(in Chinese)

[4] Morgado Dias F,Antunes A.Fault Tolerance of Artificial Neural Networks:an Open Discussion for a Global Model[J].International Journal of Circuits,Systems and Signal Processing,2010,4(1):9-16.

[5] 趙德芳,張天騏,金翔,等.基于 BP神經網絡的直擴信號擴頻碼盲識別[J].電訊技術,2010,50(10):28-35.ZHAO De-fang,ZHANG Tian-qi,JIN Xiang,et al.DSSS Signal Spread Spectrum Codes Blind Identification Based on BP Neural Network[J].Telecommunication Engineering,2010,50(10):28-35.(in Chinese)

[6] 安全,梁川,吳平.脈沖響應神經網絡的構建[J].信息與控制,2009,38(4):455-460.AN Quan,LIANG Chuan,WU Ping.Construction of Impulse Response Neural Networks[J].Information and Control,2009,38(4):455-460.(in Chinese)

[7] Jason Gauci,Kenneth O Stanley.Autonomous Evolution of Topographic Regularities in Artificial Neural Networks[J].Neural Computation,2010,22(7):1860-1898.

[8] Javier Macia,RicardV Solé.Distributed robustness in cellular networks:insights from synthetic evolved circuits[J].Journal of Royal Society Interface,2009,33(6):393-400.

[9] Sekanina L.Evolutionary functional recovery in virtual reconfigurable circuits[J].ACM Journal on Emerging Technologies in Computing Systems,2007,3(2):1-22.

[10] WANG J,LEE C H.Evolutionary design of combinational logic circuits using VRA processor[J].IEICE Electronics Express,2009,6(3):141-147.