分數微分方程邊值問題正解的存在與不存在性

李瑞瑞，劉文斌

(中國礦業大學理學院，江蘇徐州221116)

0 前言

近年來分數階微分方程問題得到了廣泛的研究，一方面是由于分數積分及微分本身的發展;另一方面是因為其在物理、化學、力學等領域的應用［1－2］。文獻［3］研究了分數階兩點邊值問題，文獻［4］利用錐拉伸與錐壓縮不動點理論討論了含參數的分數階兩點邊值問題正解的存在與不存在性。文獻［5］用錐上不動點定理，研究了奇異非線性狄利克雷邊值問題解的存在性。

本文進一步研究了下述問題:

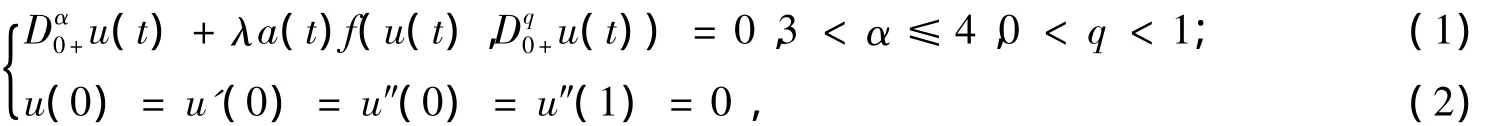
解的存在性與不存在性。其中，Dq0+是Riemann－Liouville導數;λ＞0參變量;a:［0，1］→［0，+∞)連續且不恒為零;f:［0，+∞)×［0，+∞)→［0，+∞)連續，主要利用的工具是錐拉伸錐壓縮不動點理論。

1 預備知識

定義1 函數f(x)在Riemann－Liouville意義下s階分數積分指

定義2 函數f(x)，x≥0在Riemann－Liouville意義下s階分數微分指

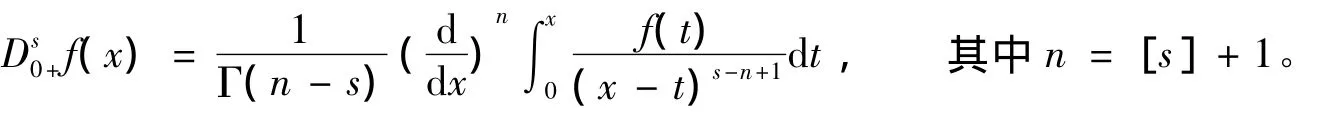
引理1 若y(t)∈C［0，1］且y(t)≥0，則分數階微分方程邊值問題

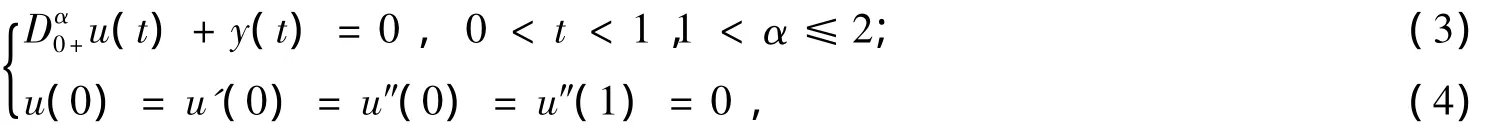
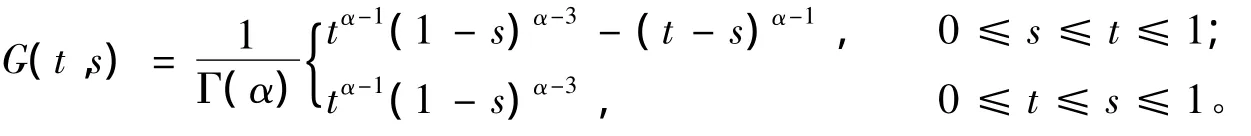
引理2 G(t，s)有下面的性質:

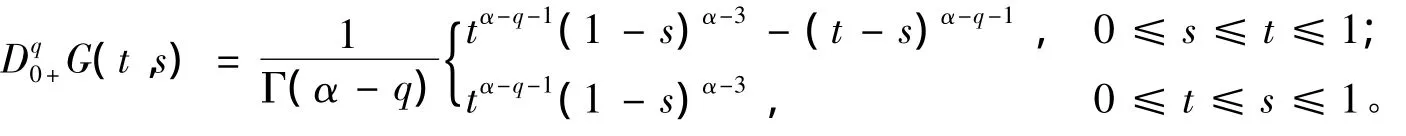
證明

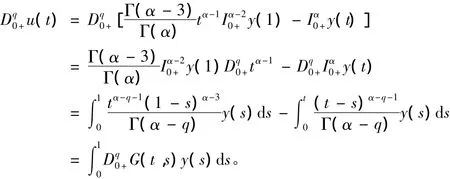
證明 證明過程類似引理2，在此略去。

引理5 設X是一巴氏空間，P是X中一個錐，設Ω1，Ω2為P中開子集，且0∈Ω1?Ω2，令T: P∩Ω1)→K為一全連續算子，若下列條件之一滿足:

(H1)當u∈P∩?Ω1時，Tu≤u;當u∈P∩?Ω2時，Tu≥u。

(H2)當u∈P∩?Ω1時，Tu≥u;當u∈P∩?Ω2時，Tu≤u。

則T在P∩(Ω2Ω1)中有一不動點。

2 主要結果

u(t)是問題(1)和問題(2)的解等價于u(t)滿足下面的積分方程:

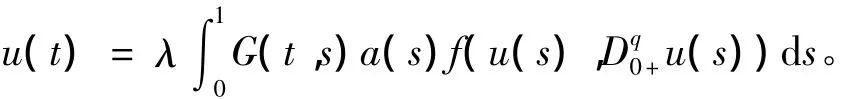
定義其上范數uX=+Du(t=u+Du，其中· 是連續函數空間中的最大值范數，則X是一個巴拿赫空間［9］。定義錐P(?X):P={u(t)∈X:u(t)+Du(t)≥uX}，

定義T:P→X，

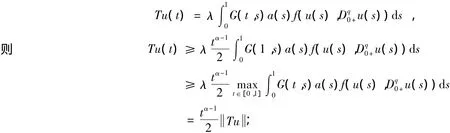
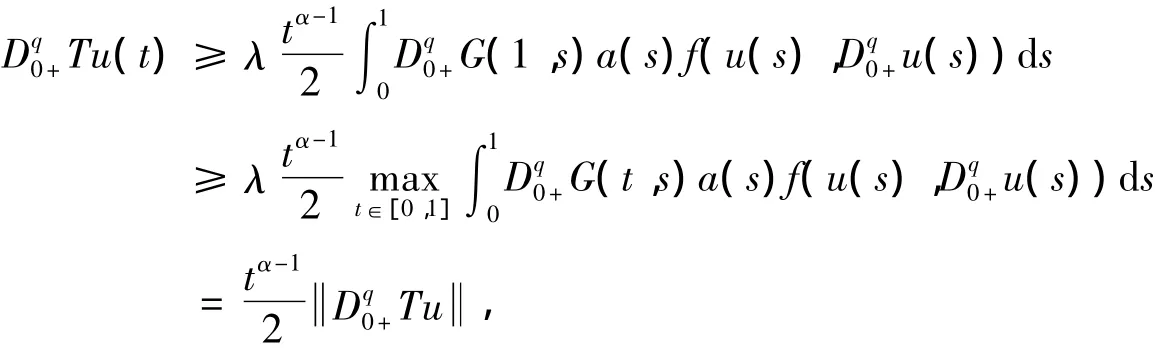
由P的定義，容易證明T(P)(?P)一致有界，且等度連續。由Arzela－Ascoli定理知:T(P)相對列緊。又T是連續的，故T是全連續的。

為行文的方便，定義下述重要的常數

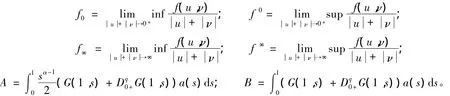
定理1 設Af∞＞Bf0，則對于λ∈)，問題(1)和問題(2)至少有一正解。

證明 取ε＞0充分小，使得(f0+ε)Bλ≤1，由f0的定義，存在l1＞0，使得當0＜+≤l1時，f(u，ν)≤(f0+ε)(+)。若u∈P且uX=l1，則

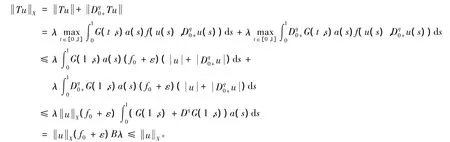
取Ω1={u(t)∈X:uX＜l1}，則由上知:當u∈P∩?Ω1時，TuX≤uX。

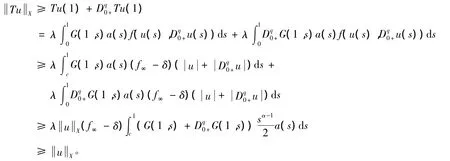
故取Ω2={u(t)∈X:X＜l2}，則Ω1?Ω2，且u∈P∩?Ω2時，X≥X。

由上，引理5中條件H1成立，所以T在P∩(Ω1)有一不動點，即為問題(1)、(2)的正解。

定理2 設Af0＞Bf∞，則對于λ∈()，問題(1)、(2)至少有一正解。

證明 取ε＞0充分小，使得(f0ε)Aλ≥1，由f0的定義，存在l1＞0，使得當0＜+≤l1時，f(u，ν)≥(f0ε)(+)。若u∈P且X=l1，則:

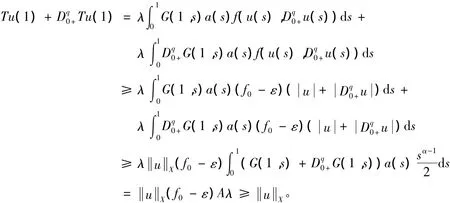
取Ω1={u(t)∈X:X＜l1}，則由上知:當u∈P∩?Ω1時，X≥X。

類似定理1，可以證明，u∈P，Ω2={u(t)∈X:X＜l2}，X=l2，即u∈P∩?Ω2時，X≤X。

由上，引理5中條件H1成立，所以T在P∩(Ω2Ω1)中有一不動點，即為問題(1)、(2)的正解，結論得證。

證明 反證:假設u是問題(1)、(2)的一個正解，則:

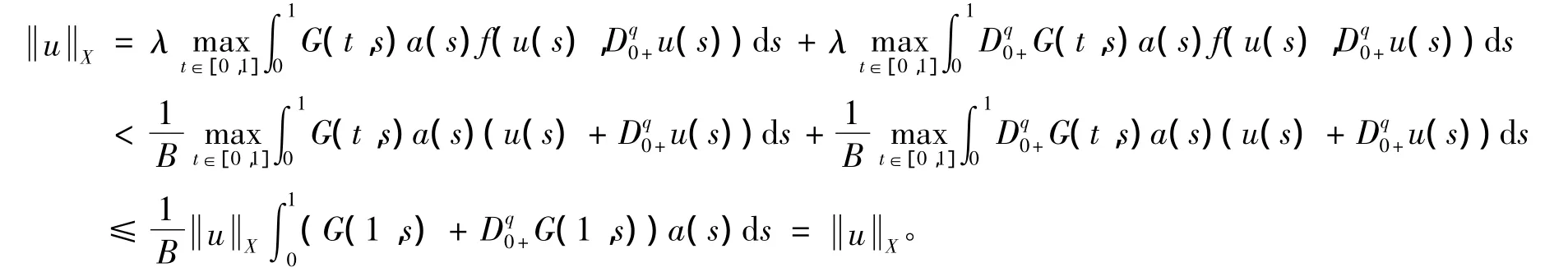
矛盾，故結論得證。

證明 反證:假設u是問題(1)、(2)的一個正解，則:

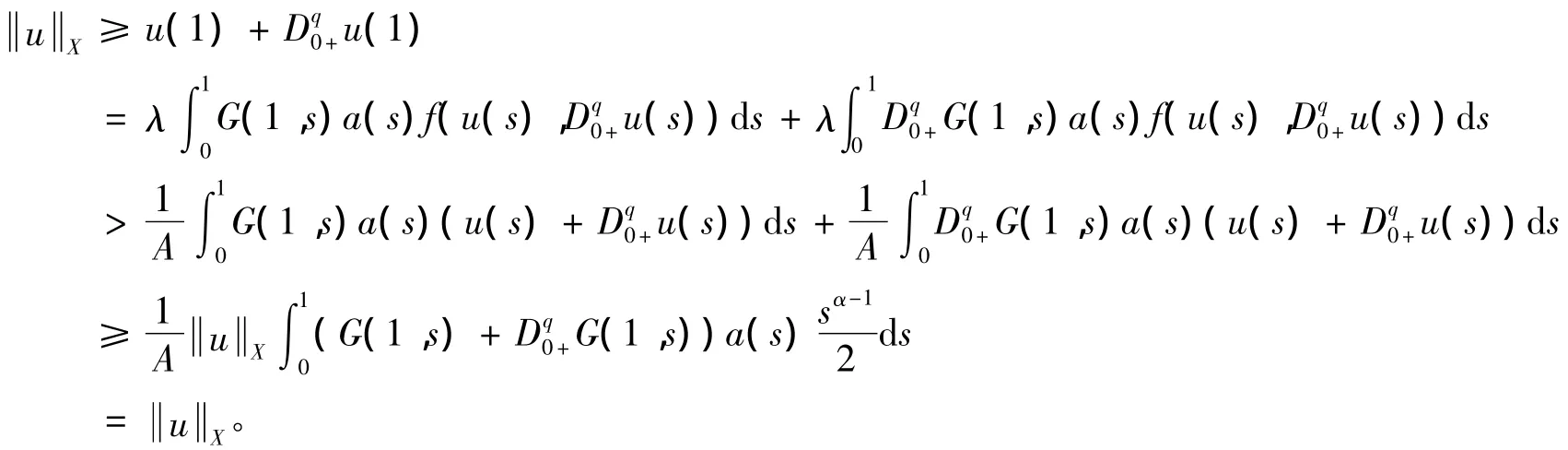
矛盾，故結論得證。

［1］ Samko SG，Kilbas A A，Marichev O I.Fractional Integrals and Derivatives:Theory and Applications［M］.Yverdon:Gordon and Breach Sci Publishers，1993.

［2］ Podlubny I.Fractional Differential Equations，in:Mathematics in Sciences and Engineering［M］.San Diego:Academic Press，1999.

［3］ Bai Zhanbing，Lv Haishen.Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation［J］.JMath Anal Appl，2005，311:495－505.

［4］ El－shahed M.Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation［J］.AIP Conf Proc，2009，1124:101－108.

［5］ Agarwal R P，O’Regan D，Stank S.Positive solutions for Dirichlet Problems of Singular Nonlinear Fractional Differential Equation［J］.JMath Anal Appl，2010，371:57－68.

［6］ Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations，in:North－Holland Mathematics Studies［M］.Amsterdam:Elsevier Science BV，2006.

［8］ Krasnosel’skill M A.Positive Solutions of Operator Equations［M］.Froningen:Noordhoff，1964.

［9］ SU Xinwei.Boundary Value Problem for a Couple System of NBonlinear Fractional Differential Equations［J］.App Math Lett，2009，22:64－69.