部分線性變系數EV模型估計的漸近正態性

馮三營，牛惠芳

(洛陽師范學院數學科學學院，河南洛陽471022)

0 前言

考慮部分線性變系數模型:

其中，Y為一維響應變量;X為p維協變量;Z為q維協變量;T為一維協變量;β為p維未知參數向量; α(T)=(α1(T)，…αq(T))τ是q維未知函數向量;ε是不可觀測的隨機誤差。

作為變系數模型和部分線性模型的推廣，模型(1)最近得到了廣泛的關注，已有大量學者進行了深入的研究，例如，文獻［1］基于局部多項式方法最早研究了該模型;文獻［2］利用小波方法估計了模型中的參數部分和非參數部分;文獻［3］基于局部線性方法提出了一種新的有效估計;文獻［4］提出了Profile最小二乘估計并且基于廣義似然比檢驗方法研究了該模型的檢驗問題。但在實際操作中，協變量X，Z往往帶有測量誤差。對協變量X帶有測量誤差的部分線性變系數模型，文獻［5］在測量誤差向量協方差陣已知的情形下，獲得了模型中參數和非參數部分的估計，并證明了估計量的相合性和漸近正態性。文獻［6］運用經驗似然方法構造了模型中參數的最大經驗似然估計及其經驗似然置信域，并證明了估計量的漸近正態性。對于協變量Z帶有測量誤差的部分線性變系數模型尚未見到相關文獻。

本文考慮協變量Z帶有測量誤差的部分線性變系數模型，運用局部糾偏方法和Profile最小二乘估計方法得到了模型中未知參數和未知系數函數的估計，并在適當條件下研究了它們的漸近性質，并對本文所提估計方法在有限樣本下的實際表現進行了數值模擬研究。

1 方法與主要結果

假設記錄數據{Xi，Wi，Ti，Yi是來自以下模型的一組獨立同分布的可觀測隨機樣本，

其中，{εi}為相互獨立的模型誤差，且E(εi)=0，Var(εi)=σ2＜∞。測量誤差{ui}獨立同分布，其均值為0，協方差為Σu，且ui與(Xi，Zi，Ti，εi)相互獨立。

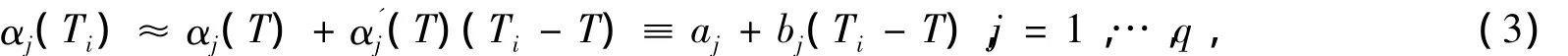
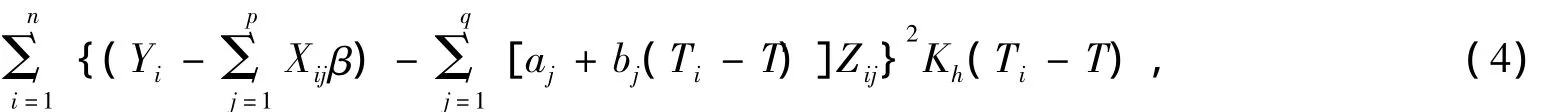
其中，K(·)為核函數;且Kh(·)=K(·/h)/h，h為收斂于零的常數，稱之為窗寬。

記Y=(Y1，…，Yn)τ;ε=(ε1，…，εn)τ;ωT=diag(Kh(T1T)，…，Kh(TnT));X=(X1，…，Xn)τ;

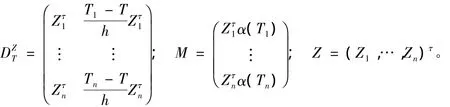
由于Zi不可觀測，如果在式(5)中直接用Wi替代Zi，則得到的估計不再是相合估計。為了消除測量誤差造成的估計偏差，借鑒文獻［7］的思想，對式(5)進行如下的局部糾偏:

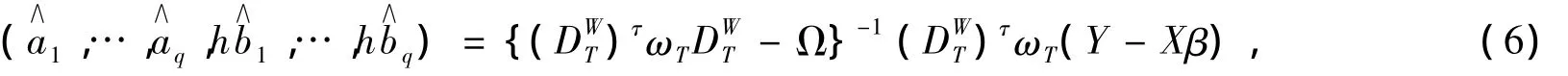
于是系數函數{αj(·)，j=1，…，q}的估計為

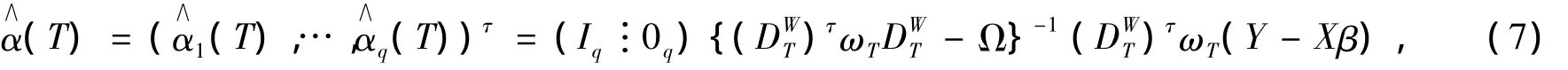
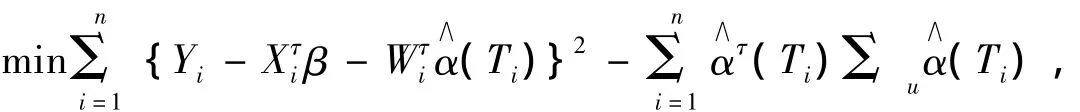
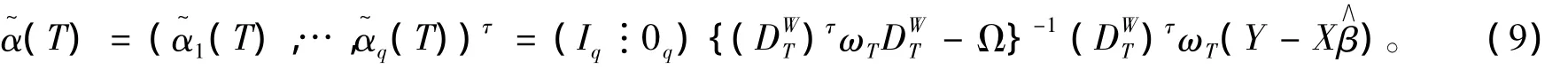
A3.{αj(·)，j=1，…，q}關于T∈有二階連續導數。

A4.核函數K(·)為概率密度函數且具有緊支撐。當n→∞時，nh2/log2n→∞，nh8→0。

A5.矩陣Γ(T)=E(Z1ZT )非退化。E(X1XT )和Φ(T)=E(Z1XT)均為Lipschitz連續。

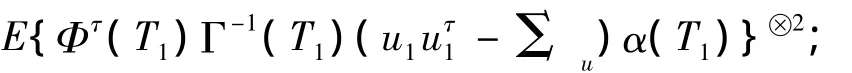
Σ1=E(X1X)E(Φτ(T1)Γ1(T1)Φ(T1));A?2表示AAτ;→L表示依分布收斂。

定理2 設條件A1～A5成立，如果α(T)是系數函數真值，則

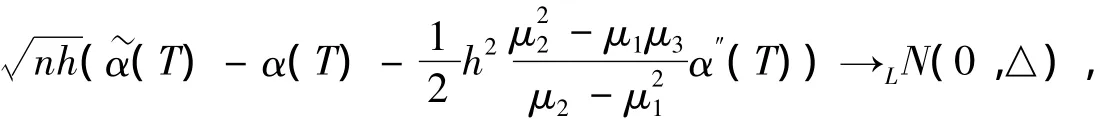
2 模擬研究

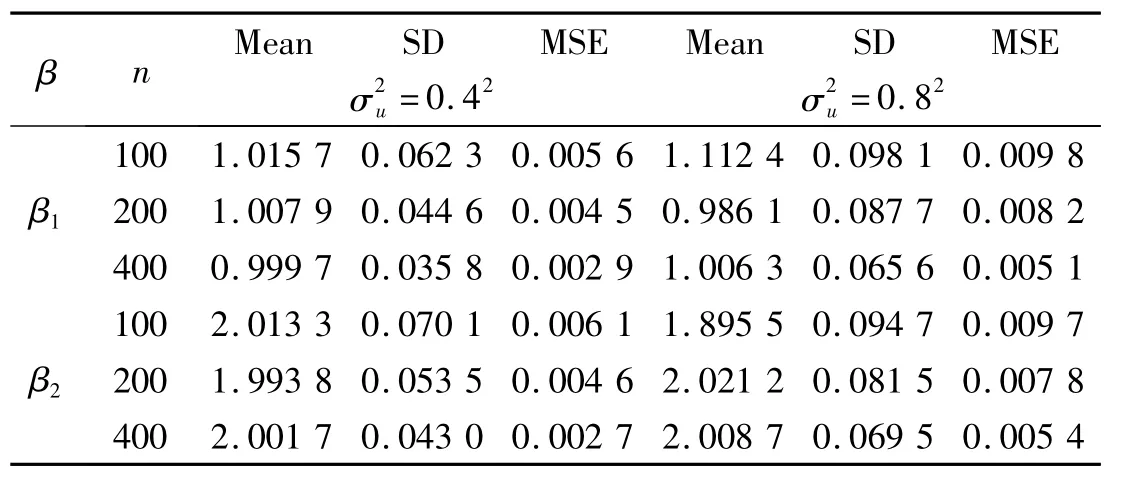
表1 參數β估計的均值、標準差與均方誤差

通過數值模擬試驗研究文中所得結論在有限樣本下的實際表現。考慮模型:Y=Xτβ+Zτα(T)+ε，W=Z+u，這里β=(1，2)τ;系數函數α(t)=2t(1t);(Xτ，Z)τ服從多元正態分布，其均值向量為(1，1，1)τ;協方差陣(σij)滿足σij=0.5|ij|。T服從區間［0，1］上均勻分布，εN(0，1)，u服從均值為0方差為σ的正態分布。在下面的模擬中，分別取樣本容量 n=100，200，400，σ= 0.42，0.82。取核函數為Epanechnikov核K(t)=0.75(1t2)，窗寬采用Cross-Validation方法進行選擇，重復模擬2 000次，計算β重復估計對應的均值(Mean)、標準差(SD)與均方誤差(MSE)。模擬結果見表1和圖1。對于系數函數α(t)，在此僅給出n=200，σ=0.42時的模擬結果，其他情形下的模擬效果圖和圖1類似。

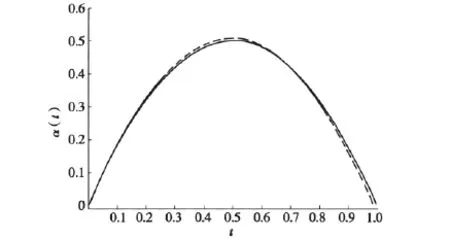
圖1 n=200，σ=0.42時，α(t)的估計曲線(虛線)和真實曲線(實線)

3 定理的證明

引理1 若條件A1～A5成立，則當n→∞時，

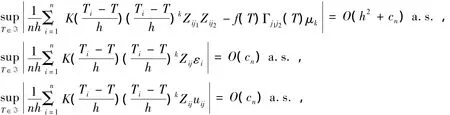
其中，j，j1，j2=1，…，q;k=0，1，2，4;Γj1j2(T)是矩陣Γ(T)的第(j1，j2)元素。

證明 見文獻［8］引理2的證明，此處省略。

引理2 若條件A1～A5成立，則

證明 見文獻［6］引理A.2的證明，此處省略。

引理3 令G1，…，Gn為i.i.d.隨機變量，若對任意s＞1，Es有界，則=o(n1/s)a.s.。

證明 見文獻［9］引理1的證明，此處省略。

引理4 若條件A1～A5成立，則

證明 類似于文獻［4］中引理7.2的證明可證明本引理，此處省略。

定理1的證明 由式(8)可知:

由引理1，引理2和引理3簡單計算可得

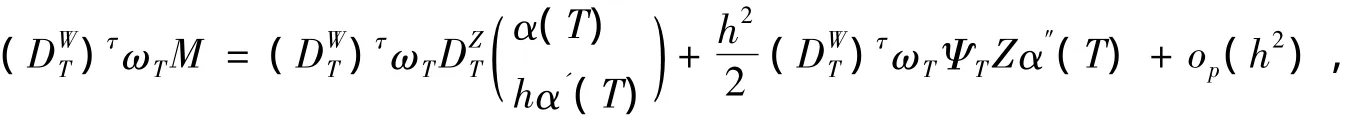
其中，ΨT=diag{((T1T)/h)2，…，((TnT)/h)2}。由引理1和引理2簡單計算可得:

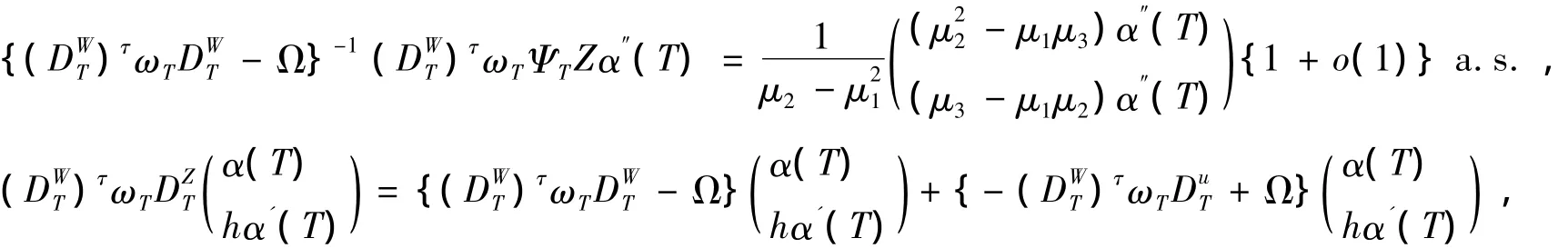
又由引理1，引理2及定理1得(Iq0q){(D)τωTDΩ}1(D)τωTX(ββ)=Op(n1/2)，故

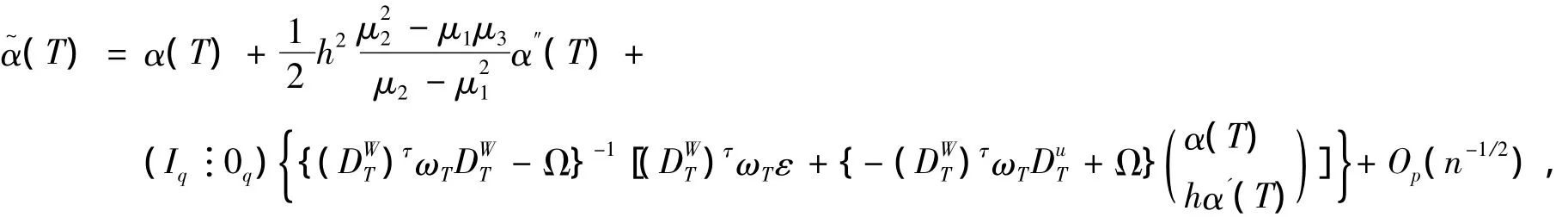
類似于文獻［7］中A4～A6式的證明，可得:

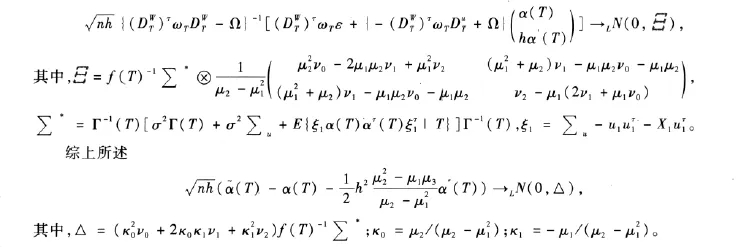
［1］ ZhangW，Lee SY，Song X.Local Polynomial Fitting in Semi-varying CoefficientModels［J］.JMultivariate Anal，2002，82: 166－188.

［2］ Zhou X，You JH.Wavelet Estimation in Varying-coefficient Partially Linear Model［J］.Stat Probab Lett，2004，68:91－104.

［3］ Xia Y C，ZhangW Y.Efficient Estimation for Semivarying-coefficientModel［J］.Biometrika，2004，91:661－681.

［4］ Fan JQ，Huang T.Profile Likelihood Inferences on Semi-parametric Varying-coefficient Partially Linear Models［J］.Bernoulli，2005，11(6):1031－1057.

［5］ You JH，Chen G M.Estimation of a Semi-parametric Varying-coefficient Partially Linear Errorsin-variables Model［J］.J Multivariate Anal，2006，97:324－341.

［6］ Wang X L，Li G R，Lin L.Empirical Likelihood Inference for Semi-parametric Varying-coefficient Partially Linear EV Models［J］.Metrika，2011，73(2):171－185.

［7］ You JH，Zhou Y，Chen G M.Corrected Local Polynomail Estimation in Varying Coefficient Models with Measurement Errors［J］.The Canadian Journal of Statistics，2006，34:391－410.

［8］ Xia Y C，LiW K.On the Estimation and Testing of Functional-coefficient Linear Models［J］.Statistics Sinica，1999，9:737－757.

［9］ Shi J，Lau T S.Empirical Likelihood for Partially Linear Models［J］.JMultivariate Anal，2000，72(1):132－148.

［10］ Li L，Greene T.Varying Coefficients Model with Measurement Error［J］.Biometrika，2007，84:1－8.

［11］ Xue LG，Zhu L X.Empirical Likelihood for a Varying Coefficient Model with Longitudinal Data［J］.JAm Statist Ass，2007，102:642－654.