分析水中結構自由振動的三維附加質量矩陣法

張文鵬 宗 智

大連理工大學工業裝備結構分析國家重點實驗室運載工程與力學學部 船舶工程學院，遼寧 大連116024

分析水中結構自由振動的三維附加質量矩陣法

張文鵬 宗 智

大連理工大學工業裝備結構分析國家重點實驗室運載工程與力學學部 船舶工程學院，遼寧 大連116024

船舶總體振動分析需考慮對船體外部水的影響。通過建立水域三維有限元模型進行計算或者先計算出附加質量后，加入到結構質量中進行計算。隨著有限元技術的發展，船舶大都采用三維有限元建模。傳統方法，例如劉易斯附加水質量法，雖然考慮到縱向變形，但確沒有忽略船體橫剖面的變形，因而不夠準確。采用三維邊界元方法，考慮水中結構振動的三維效應，計算三維附加質量矩陣，并對水中結構振動進行分析。結果表明，水中結構振動是三維變形，應該采用三維附加質量矩陣進行振動分析。

水中結構；三維附加質量矩陣；自由振動分析；濕模態

1 引言

船體是一種復雜的彈性結構，船舶在航行過程中會受到各種激振力的作用而產生不同程度的振動，例如波浪激勵振動，主機、螺旋槳激勵引起的振動等。因此，能夠準確預報船體結構振動的固有頻率及響應，從而避免共振并降低振動響應，對于船舶設計而言十分重要。相關研究也有許多，例如Lin等［1］研究了復雜船體結構振動特性和振動的控制，Franois等［2］研究了主機和螺旋槳對船體及上層建筑的影響。

船舶是在水中航行，因此在對船舶總體振動進行分析時，要考慮水對水中結構振動造成的影響。孫士麗等［3］采用濕模態方法對單面浸水的板、加筋板的振動特性進行計算。吳芳等［4］通過Ansys計算擬合了單面浸水板的附加質量系數曲線，并計算了單面浸水板的固有頻率。夏利娟等［5］通過二維有限元法和二維邊界元法，分別計算船體結構和流體，并計算了高速船的垂向振動。孫洋等［6］采用劉易斯方法計算了船體總體振動固有頻率，對水平彎曲—耦合振動進行了修正，并給出了修正系數。文獻［7］采用改進二維邊界元法，計算無限流場中不規則截面物體的附加質量。

對于復雜的彈性結構的振動問題，需要采用數值計算方法進行分析。通用有效的數值方法是有限元法［8］，目前船舶大都采用三維有限元建立模型。考慮到水對船體振動造成的影響，可以采用建立結構和水域的三維有限元模型進行整體計算；或者先計算出水中結構附加質量，然后加入到結構質量中進行計算。文獻［9］就是采用建立結構和水域的三維有限元模型的方法，研究了空氣和水中多艙段復雜殼體的振動模態特性。

計算附加質量的方法，只需考慮固液交界面的流體，計算量小且計算效率高。但目前國內對于附加質量對水中結構振動的影響的處理，基本都是采用劉易斯附加水質量法或者二維邊界元方法。這些方法將船體看作自由梁，假設每一個橫剖面都在做剛體運動，然后采用劉易斯或者二維邊界元方法計算出每個剖面作剛體運動的附加質量，沿船長積分得到整船的附加質量。再將整船的附加質量除以船體濕表面積，得到附加水密度，加到船體與水接觸的外板的密度上，然后分析船體振動。該方法考慮了沿船長方向結構變形的影響，但是未計及沿橫剖面結構變形產生的影響。

現在的有限元建模并不是簡化成梁模型，而是更為復雜的三維模型。在橫剖面上兩個單元之間的相對變形會對流體產生影響，如果不考慮這種影響，而將橫剖面視為剛體，采用劉易斯法或者二維邊界元方法，從理論上講是錯誤的。

本文采用三維邊界元方法計算水中結構的附加質量矩陣。首先，考慮三維結構變形與流體的耦合效應及對附加質量的影響，使得進行水中結構自由振動分析更加準確。然后，對三維附加質量矩陣和理論解進行了對比驗證，結果證明所計算的三維附加質量矩陣是正確的。在此基礎上，采用濕模態法進行水中結構自由振動分析，計算了在水中自由振動的固有頻率以及振型。

2 附加質量矩陣計算及濕模態理論

1978年，Deruntz等開始采用邊界元方法計算無限流場中結構振動的附加質量［10］。本文也采用邊界元方法，來計算流場中結構的附加質量矩陣。

2.1 流場中速度勢及其導數

假定流體是無粘、無旋、不可壓縮的理想流體，定義無限流場速度勢：

速度勢的定解問題為：

上面定解問題的解，可以采用簡單格林函數分布源模型來表達，并假定采用常數源，即在每個劃分的濕表面單元上源強是固定值：

式中，q為源點；p為場點；σ（q）為源的強度；S為物體表面；G（p，q）為格林函數。

對于無限水域，格林函數為：

速度勢及其導數為：

當水中結構物離水面比較近或者結構物為水面漂浮結構物時，需要考慮自由面的影響。對于較高頻率的振動，自由面波動的影響可忽略不計，此時速度勢的定解問題為：

在這種定解條件下，格林函數為：

這樣，速度勢及速度勢的導數為：

式中，q是q點關于自由水面的鏡像點。

2.2 流體質量矩陣

在流域內，流體動能為：

若取結構外法向（即指向流體域內）為正，則流體動能為：

在物體的表面上劃分網格，則流體的動能可以表示為離散形式：

式中，φn、φ、p為相應于離散的濕表面的列向量；長度等于濕表面數量n；dS為n×n的對角矩陣。上標T表示轉置。

對于常數源，速度勢及其導數可以寫成離散形式：

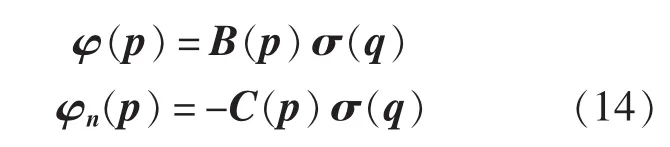
式中，σ（q）為n個元素的列向量；B（p），C（p）為n×n的滿陣；p為流場內任意一點，當場點p位于濕表面單元的控制點P，即p＝P時有：

將式（14）和式（15）代入式（13），可得：

式中，

式中，C－T＝（C－1）T。由于當任意向量A非對稱時，uTAu＝0，所以式（16）可以寫成：

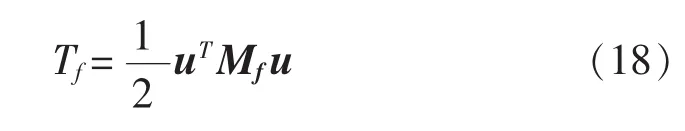
式中，

將Mf稱為流體質量矩陣，或者附加質量矩陣。

2.3 水中結構濕模態

流體速度u和結構速度x˙有如下關系：

式中，D為流體單元與結構自由度的變換矩陣。將式（20）代入式（18），得

式中，Ma＝DTMfD

式（21）表明，相對應于結構的位移x、速度x˙和加速度x¨，流體的相當質量矩陣為Ma。

對于無阻尼結構振動自由振動，有如下方程

則水中無阻尼結構振動自由振動濕模態方程為：

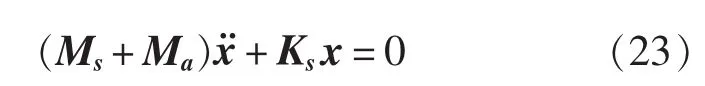
3 附加質量矩陣計算驗證

為驗證附加質量矩陣計算是否正確，引入流體邊界模態［11］：

式中，Af為濕表面單元面積對角陣。通過計算特征值λ，就可以驗證附加質量矩陣。

以無限流場中的圓球為例，計算驗證附加質量特征值。無限水域中球體振動特征值精確解為：

首先，建立無限流場中的半徑為10的球體模型，并采用4個網格劃分方案，計算了4種網格方案的流體邊界模態特征值，并與理論解進行比較，以考察計算的誤差及收斂性。圓球的模型及網格情況如圖1所示，分別劃分600、1 176、1 944和2 904個單元。

計算時，n取0，1，2，3，4，分別計算相應理論解和計算值，并進行比較。計算結果見表1和圖2。

圖1 圓球模型及網格Fig.1 Sphere model and its mesh

表1 無限流場中球體邊界模態特征值計算及與理論解比較Tab.1 Sphere boundary modal eigenvalue calculation and comparison with theoretical solution in infinite field

圖2 特征值誤差隨網格數變大而減小Fig.2 Eigenvalue calculation of the convergence

從計算結果來看，對于同一個單元數，0階模態和4階模態的相對誤差比較小，2階或者3階模態的相對誤差最大。對于不同單元數，單元數越小，相對誤差越大，相對誤差最小的是2 094單元的情況，其最大相對誤差為1.919%；相對誤差最大的是600單元的情況，但其最大相對誤差也只有4%，這個相對誤差是在工程允許范圍內的。隨著網格單元數的變大，相對誤差減小，說明計算是收斂的。

4 應用三維附加質量矩陣計算水中結構振動

在驗證了三維附加質量矩陣后，根據濕模態理論就可以進行水中結構的自由振動分析，計算水中結構的固有頻率。計算流程為如圖3所示。

以一個盒子為例代表船舶，計算其固有頻率。盒子的基本參數列于表2中，盒子建模見圖4。

計算情況如下，分別計算了盒子在空氣中和水中的固有頻率及振型，圖5給出了前7階的振型，表3給出了前10階的固有頻率。

圖3 應用附加質量矩陣計算結構水中振動流程圖Fig.3 Flow chart of calculation of free vibration of structure in water with added mass matrix

從計算結果來看，結構在水中的固有頻率要比在空氣中低，降幅從15%～38%不等，平均降幅為24.78%。水中結構的振型與空氣中的振型會產生交錯，例如圖5中的（d）和（e）：在空氣中圖5中的（e）是在第3階出現的振型，而在水中，圖5中的（d）則在第2階就出現了。

表2 盒子的基本參數Tab.2 Main particulars of a box

圖4 盒子模型Fig.4 Box model

圖5 盒子在空氣中及水中前7階的振型Fig.5 1st～7thmodal natural vibrations of box in the air and water

表3 盒子在空氣中及水中固有頻率Tab.3 Natural frequency of box in the air and water

5 結論

本文采用邊界元方法計算水中結構三維附加質量矩陣的結果可靠，通過計算無限流場中球的附加質量矩陣，其特征值與理論解的最大相對誤差為4%，滿足工程精度。同時，隨著網格的加密，相對誤差減小，計算是收斂的。

其次，結構在水中的固有頻率要比在空氣中低，降幅從15%～38%不等，平均降幅為24.78%。水中結構的振型與空氣中的振型會產生交錯，在空氣中較高階數的振型在水中會提前在較低階數出現。

最后，從計算的水中結構振型來看，橫剖面會產生變形，即結構濕表面變形呈三維。因此，進行三維水中結構振動分析時，應當采用三維附加質量矩陣。

［1］LIN T R，PAN J，O＇SHEA P J，et al.A study of vibration and vibration control of ship structures［J］.Marine Structures，2009，22（4）：730－743.

［2］FRANOIS B，LUDOVIC J，LECH M，et al.Evaluation of main engine and propeller excitations of ship hull and superstructure vibration ［J］.InternationalShipbuilding Progress，2008，55（1－2）：3－27.

［3］孫士麗，王詩平，姚熊亮，等.板和加筋板流固耦合振動特性研究［C］.黑龍江省造船工程學會2008年學術年會論文集.黑龍江，哈爾濱，2008.

［4］吳芳，趙德有.水對船舶與海洋建筑物結構振動影響的研究［J］.中國海洋平臺，2007，22（3）：22－26.

［5］夏利娟，吳衛國，翁長儉，等.高速船垂向振動計算的流固耦合分析［J］.上海交通大學學報，2000，34（12）：1713－1716.

［6］孫洋，趙德有.流固耦合理論在船體總振動附加水質量研究中的應用 ［J］.中國海洋平臺，2008，23（3）：22－27.

［7］李華東，朱錫，羅忠，等.附連水質量的邊界元法求解［J］.海軍工程大學學報，2009，21（2）：45－49.

［8］金咸定，趙德有.船體振動學［M］.上海：上海交通大學出版社，2000.

［9］陳明，錢家昌，曹為午.不同介質中多艙段復雜殼體的振動模態特性研究［J］.噪聲與振動控制，2009，29（2）：1－5.

［10］DERUNTZ J A，GEERS T L.Added mass computation by the boundary integral method［J］.International Journal for Numerical Methods in Engineering，1978（12）：531－550.

［11］GEERS T，DOUBLY L.Asymptotic approximations for transient motions of submerged structures［J］.Journal of the Acoustical Society of America，1978，64 （5）：1500－1508.

3D Analysis Method for Added Mass Matrix about Free Vibration of Structure in Water

Zhang Wen-peng Zong Zhi
School of Naval Architecture Engineering，Faculty of Vehicle Engineering and Mechanics，State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，DaLian 116024，China

In analysis of ship global vibration，influence of outboard water should be considered.For studying the global vibration，two methods can be used.One is that 3D finite element model of water domain is applied，and the other is that added mass is introduced into structural matrix for calculation. With the finite element technique developing，3D finite element model of ship is usually taken.However，it is not correct for traditional method（such as Lewis added mass method）to neglect the deformation of ship transverse section.We proposed a kind of boundary element method to calculate the 3D added mass matrix of structure with 3D effect，and analyzed the wet structural response.The results show that the method is available and accuracy.

structure in water；3D added mass matrix；free vibration analysis；wet mode

U661.44

：A

：1673－3185（2011）04－13－06

2011-04-08

創新研究群體科學基金（50921001）；國家重點基礎研究發展計劃項目（2010CB832700）

張文鵬（1980－），男，博士研究生。研究方向：水下爆炸、流固耦合、船舶水動力學、結構振動。E-mail：zwp_ln＠163.com

宗 智（1964－），男，教授，博士生導師。研究方向：水下爆炸、流固耦合、水動力學、結構沖擊、計算力學。E-mail：zongzhi＠dlut.edu.cn

10.3969/j.issn.1673-3185.2011.04.003