低能光子的量子引力“遺跡”效應

邵立晶，馬伯強

(北京大學物理學院，北京100871)

隨著人們對于各類對稱性與對稱性破缺的深入理解，以及量子引力理論發展的需要，物理學家開始考慮在極高能量下洛倫茲對稱性存在著破缺的可能性。 倘若量子引力能標1.22×1019GeV下存在著洛倫茲破壞行為，那么，在低能下就會有微小的殘留“遺跡”效應，比如說，對正則能動量色散關系E2＝p2＋m2會產生一個小的修正。進一步地，這修正將體現出低能下豐富多彩的量子引力現象學，為量子引力理論的實驗探索提供了一個寶貴的窗口[1]。

雖然洛倫茲破壞即使存在，修正項也會由于普朗克物理的壓低而很小，可是，令人感到幸運的是，自然界存在一定的機制來“放大”量子引力的效應，如，長基線的宇宙距離的傳播，超精準地球實驗的測量等。 同時，如今的地球實驗與天文觀測的技術發展，在精度上已部分達到探測量子引力“遺跡”的能力，并在未來的實驗裝置中將有更好的改進。這些觀測可用來探測與約束洛倫茲破壞效應，并以此來區分、檢驗或約束量子引力理論。

本文討論了在量子引力唯象學領域最熱門的“標準模型拓展”以及在此框架下的光子的色散關系。進一步地，文章研究了量子引力在天體物理的高能光子領域上所體現出的效應，并與最新的實驗相結合，對量子引力理論進行一定的檢驗與約束。

1 量子引力理論與光子的色散關系

不同的量子引力理論給出了不同的預言，如弦論[2]、時空泡沫理論[3]、圈引力理論[4]和非對易幾何場論[5－7]等。 一般來說，它們都會給出對標準的能動量色散關系E2＝p2＋m2的修正，可是具體的修正項與修正行為有所不同，所以能夠從實驗上加以區分與鑒別。

對于洛倫茲破壞物理的描述，最直接與最有效的出發點就是把洛倫茲破壞項納入到標準模型這個“有效量子場論”的框架中。 Colladay和Kostelecky做了這方面最成功的嘗試，系統地發展了“標準模型拓展”[8－9]，這是 SU(3)?SU(2)?U(1)對稱性下的標準模型的最小擴展。擴展的拉氏量中引入了直接破壞洛倫茲對稱性的“洛倫茲破壞項”。這些項可以看成是從高能標到低能標時“對稱性自發破缺”而導致張量場獲得真空期望值，并進一步與標準模型中的場量耦合。模型保留了標準模型中的很多好的性質，如規范不變性、能動量守恒、洛倫茲協變性、微觀因果性、能量的正定性和反常相消等。而且，由于這個拓展的理論并沒有離開大家比較熟悉的量了場論的框架，理論的預言與實驗觀測檢驗也比較方便，所以，很多研究集中于此。

Colladay和Kostelecky初步研究的“標準模型拓展”是可重整的有效場論，他們的做法十分直觀有效。他們把張量場由于洛倫茲自發破缺導致的真空期望值作為拉氏量中的常數系數，通過引入它們與標準模型的場量的耦合，這些項將展現出洛倫茲破壞的物理，例如，對于光子場而言，所有可重整的洛倫茲破壞算符可通過對稱張量（kF）κλμν與反對稱張量（kAF）κ引入。具體來說，純光子部分的拉氏量為[8，9］，

其中，(kF)κλμν部分是 CPT 為正的，而(kAF)κ部分破壞了CPT對稱性，是CPT負的。要注意的是，這個拉氏量中的系數kA與kAF，雖然也帶有洛倫茲指標，但與其他的場量不同，它們是破壞了洛倫茲協不變性的。從形式上來看，可以很容易看出它們保持了理論的洛化茲協變性；直觀地說，也就是保持了上下指標的有效收縮。所以，新引入的洛倫茲破壞項，在粒子的洛倫茲變換下，它們作為背景常場量，是不變的，而對于坐標第的變換，它們是與其他的張量一樣變化的；這就是引入洛倫茲破壞項的關鍵點。同樣，通過與上面一樣的方法，也可以引入標準模型的其他成分[8－9]。

其后，Myers，Pospelov[10]和Mattingly等人系統地研究了不可重整的“標準模型拓展”。不可重整的理論的好處在于，在拉氏量中引入的修正項是直接受到普朗克能量壓低的，人而能夠更加自然地給出“微小”的洛倫茲破壞效應，在無量綱耦合系數量級為O(1)情況下，能夠與實驗和觀測沒有嚴重的沖突。不可重整的理論給出了更好的普朗克能標壓低的機理。所以，近些年的研究，對于不可重整的量子場論也有了很多的涉及與討論。

對于質量量綱為5-維的標準模型拓展，依據拉氏量在CPT變換下的行為，我們可以把這些5-維的不可重整項分為CPT為廳和CPT為偶兩大類[11]。CPT為廳的光子修正項可寫為[11－12]

其中的u是個固定的類時四矢量，表明了特殊的參考系方向，F～的定義為F～μν=∈μνρλFρλ/2；PR，L=(1±γ5)/2是左右手投影算符，Dμ＝?μ＋ieAμ是QED中的協變微商；ξ，δR，L和ζR，L是量級為 O(1)的洛倫茲破壞系數；另外，LV-中的“-”號表示CPT為奇，后面類似的“+”號表示CPT為偶。CPT為偶的5-維的光子修正項并不存在，即另外，Mattingly給出了空間旋轉不變情形下的6-維質量量綱的洛倫茲破壞的光子項[11－12]

通過5-維，或者6-維的拉氏量，我們可以得到相應情況下的光子能動量色散關系[12]

其中，n＝5表示5－維情況，n＝6表示6－維情況。在有效場論中，這就意味著5－維洛倫茲破壞項會導致雙折射現象[13]。

2 光子傳播時延

可以看到，在量子引力理論中，傳統的色散關系可能會受到微小的修正。正是這微小的修正，衍生出了豐富多彩的洛倫茲破壞唯像學研究。在洛倫茲破壞修正的色散關系下，我們假設粒子速度v＝?E(p)/?p仍舊成立的話，那么，對于光子來說，我們就會有非恒定的光速，寫成泰勒展開形式，有

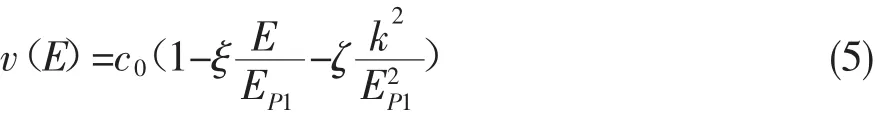
其中，ξ和ζ是洛倫茲破壞產生的修正系數，對應于前面理論中的洛倫茲破壞參數。現在的實驗與觀測傾向于排除它們為負數的情況。如果它們是正數的話，就意味著越高能量的光子，速度越慢。而另一方面，如果ξ≠0的話，那么，ζ項的修正完全可以忽略。

由于光子的速度對于能量有所依賴，那么對于同時發射的不同能量的光子，經過一定的距離所消耗的時間會有所不同。我們這里感興趣的是宇宙學距離上的光子傳播。考慮到宇宙的膨脹效應，能量為Eh的“高能光子”相對于能量為E1的“低能光子”有個洛倫茲破壞導致的時間延遲[14]，

下面考慮這個效應在γ-暴 (GRB)觀測中的應用。 近來由于觀測上的進步，如Swift衛星與Fermi衛星等的上天，GRB的研究有了實質性的突破進展。特別是，Fermi衛星的LAT裝置的探測能量達到300 GeV以上，使得GRB的高能研究成了一個有堅實觀測實事基礎的領域。同時，GEB的高能端的研究也能用來檢驗與約束新物理，洛倫茲破壞就是其中著名的一例。Amelino－Camelia等人[3]首先提出了通過伽瑪暴的精細的光變曲線與宇宙學距離的放大來檢驗洛倫茲破壞效應導致的光速對于能量的依賴關系。這里主要的出發點是從方程(6)引入的洛倫茲破壞延時，來看看是否真的在伽瑪暴的光變曲線中存在。

可是，由于伽瑪暴的光變曲線非常復雜，所以高能光子對于低能光子的延時的測量是個比較不確定的事情，容易引入人為的偏見，也可能存在儀器測量上的不確定性。就比如在GRB 090510的討論中，就涉及了各種可能用來確定洛倫茲破壞延時的可能性[15]。為了討論上的一致性，選取了Fermi LAT中的最高能量光子相對于Fermi GBM裝置的觸發光子的延時。由于GBM裝置的觸發閾值為0.1 MeV，而最高能量的光子在幾個或者幾十個GeV的量級上，所以，在方程(6)中，可以把E1近似取為零[17]。

Fermi LAT裝置由于只能探測到非常高能量的伽瑪暴，所以它大致上每個月能夠探測到一例。另外，在分析中又需要伽瑪暴的紅移（距離）信息，而紅移的測量又是需要其他的天文觀測裝置的及時跟進。所以，Fermi LAT測量到的伽瑪γ－暴中滿足我們需要的并不多。后面的討論基于有距離信息z的4個Fermi LAT的高能伽瑪暴，GRB 080916C， GRB 090510， GRB 090902B， GRB 090926A。

假設觀測到的高能光子對于低能光子的延時效應全部由洛倫茲破壞效應提供，即

那么，根據方程(6)，可以分別得到洛倫茲破壞對于能量是線性依賴以及平方依賴兩種情況下的洛倫茲破壞能標EQG，L和EQG，Q。從計算結果中我們看到[17]，不同的伽瑪暴的延時效應給出的洛倫茲破壞的能標是不同的，甚至在數量級上有所差異。如，使用最小二乘法線性回歸后，可以看到，線性能量依賴情況下的洛倫茲破壞能標為[16]

平方能量依賴情況下的洛倫茲破壞能標為[17]

從上面兩個旨果中可以看到，不同伽瑪暴所預言的能量大小之間存在很大的差異[16－17]。這里，就反應出理論的不自洽性或者唯象模型中缺少著重要的因素。

在上面的討論中，有個非常強的假設，就是這些γ－暴中的高能光子與低能光子是同時發射的。但是，這些光子是否是同時發射的呢？這還是一個非常頭疼的天文問題。事實上，研究γ－暴的輻射機制的科學家們，對于γ－暴輻射的問題，還沒有一個非常好的共識。另一方面，從方程(8)和方程(9)中，可以看到，使用簡單的假設，也就是方程(7)，得到的結論比較分散，對中心值的集中很弱。出于以上兩點考慮，有必要引入伽瑪暴的天體物理源輻射機制對于高級光子與低能光子的延遲的影響。2006年，Ellis等人首先做了這方面的嘗試，分析了BATSE，HETE和Swift的伽瑪暴的高能延遲現象[18]。但當時的數據并沒有明確的高能延遲現象的觀測，所以，他們的結論給出的洛倫茲破壞的能標的可信度不高。現在，由于有了Fermi LAT的高能光子的觀測，已經明確看到了高能光子相對于低能光子的延遲，那么，就有必要真正認真地考慮一下這樣的觀測能夠給出什么樣的洛倫茲破壞能標[16]。

在考慮源效應的分析中，最主要的出發點是，洛倫茲破壞下光子傳播的延時是隨距離面暗增大的，因為它是一種傳播“引力介質”的效應；而源方面的延遲則可以近似為與距離無關的一個常數Δtin。這樣，方程(7)應該修改為

經過一些簡單的代數操作，可以把上式轉化為［16－18］

其中，

從方程(11)中可以看到，這是一個簡單的直線方程，除了截距與斜率未知外，其他都是已知量；而截距代表的是源內部的效應，斜率是洛倫茲破壞能標的倒數或者數的平方。

因為源內部的延遲可能與伽瑪暴的內部類型有關，從而預期長暴 (GRB 080916C，GRB 090902B，GRB 090926A)與短暴(GRB 090510)會有不同的內部延遲時間Δtin。從擬合結果可以看到[16]，長暴與短暴兩種情況下，結果偏離直線的程度非常之小 (特別是只考慮長暴的情況)。具體的分析可以得到[16]，如果只考慮長暴，

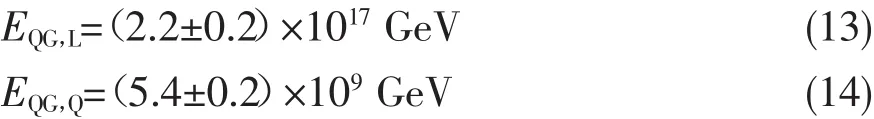
如果把短暴也考慮在內，得到的結果仍舊十分類似，而不確定性(誤差)有所增大[17]，

從上面的結果與前面不考慮源效應的結果對比分析可見，理論誤差的減小是十分明顯的。這說明了考慮源效應確實帶來了一定的優越性，這樣情況下的模型與真實的物理觀測有更好的一致性。

3 總結

洛倫茲破壞的研究是出于對標準模型與廣義相對論理論存在著嚴重的沖突的考慮，也是對新物理—量子能上能下力理論—的有益探索。很多的洛倫茲破壞下放都給出了修正的能動量色散關系，從而導致了豐富多彩的洛倫茲破壞唯心論像學。而到關重要的是，這些現象中有很多是可以通過地面實驗或者天文觀測來檢驗的，從而能夠使得背后吏深屋次的量子引力理論受到部分的檢驗。這無疑是激動人心的物理探究領域。

這方面的研究是近10年內才特別地興盛起來的，并迅速吸引了很多物理學家的極大關注。從理論方面說，這里還有很多的理論問題與檢驗問題需要澄清與探討；可幸的是，從實驗與觀測方面來說，隨著現在的實驗觀測技術的改進與新興的觀測平臺的發展，如Fermi衛星，Pierre Auger和HESS望遠鏡等，洛倫茲破壞物理有望在近10年內有重大的進展，為人類進一步認識時空的基本性質做出貢獻。

參孝文獻

[1]Mattingly D.Modern tests of Lorentz invariance[J].Living Rev Rel，2005，8：5-84.

[2]Kostelecky V A，Samuel S.Spontaneous breaking of Lorentz symmetry in string theory[J].Phys Rev，1989，D39：683-685.

[3]Amelino-Camelia G.Potential sensitivity of gamma-ray burster observations to wave dispersion in vacuo[J].Nature，1998，393：763-765.

[4]Gambini R，Pullin J.Nonstandard optics from quantum spacetime[J].Phys Rev，1999，D59：124021.

[5]Amelino-CameliaG，Majid S.Wavesonnoncommutativespacetimeandgamma-raybursts[J].Int J ModPhys，2000，A15：4301-4324.

[6]Garroll S M.Noncommutative field theory and Lorentz violation[J].Phys Rev Lett，2001，87：141601.

[7]Lukierski J，Ruegg H，Zakrzewski W J.Classical and quantum mechanics of free κ-relativistic systems[J].Ann Phys，1995，243：90-116.

[8]Colladay D，Kostelecdy V A.CPT violation and the standard model[J].Phys Rev，1997，D55：6760-6774.

[9]Colladay D，Kostelecky V A.Lorentz-violating extension of the standard model[J].Phys Rev，1998，D58：116002.

[10]Myers R C，Pospelov M.Ultraviolet modifications of dispersion relations in effective field theory[J].Phys Lett，2003，90：211601.

[11]Shao L，Ma B-Q.Lorentz violation effects on astrophysical propagation of very high energy photons[J].Mod Phys Lett，2010，A25：3251-3266.

[12]Liberati S，Maccione L.Lorentz violation：motivation and new constraints[J].Ann Rev Nucl Part，2009，Sci59：245-267.

[13]Shao L，Ma B-Q.Lorentz violation induced vacuum birefringence and its astrophysical consequences[J].Phys Rev，2011，D83：127702.

[14]Jacob U，Piran T.Lorentz-violation-induced arrival delays of cosmological particles[J].J Cosmol Astropart Phys，2008，0801：031.

[15]Abdo A A.A limit on the variation of the speed of light arising from quantum gravity effects[J].Nature，2009，462：331-334.

[16]Shao L，Ma B-Q.Lorentz violation from cosmological objects with very high energy photon emissions[J].Astropart Phys，2010，33：312-315.

[17]Xiao Z，Ma B-Q.Constraints on Lorentz invariance violation from gamma-ray burst GRB090510[J].Phys Rev，2009，80：116005.

[18]Ellis J.Robust limits on Lorentz violation from gamma-ray bursts[J].Astropart Phys，2006，25：402-411.