基于網絡能量的電力系統失步解列方案

盧芳，于繼來

(1.哈爾濱工業大學 電氣工程及自動化學院，黑龍江 哈爾濱150001;2哈爾濱工程大學 自動化學院，黑龍江 哈爾濱150001)

我國正在形成全國聯網的巨型電力系統，電網互聯在帶來巨大經濟效益的同時也使暫態穩定問題變得更為突出.當電力系統受擾進入緊急狀態時，應采取緊急控制措施，如果這些措施未能采取或不能奏效，此時應采取解列等措施，將系統中盡可能多的部分從大范圍的停電中挽救過來.目前為止解列仍然是保證系統不致完全崩潰的最后一道防線，并在我國電網中得到了廣泛應用［1-2］.

當系統發生失步以后，其聯絡線上的相關電氣量都隨之發生振蕩.其中電壓、相角、電流的變化特征已被廣泛應用于傳統的失步解列裝置中［3-4］，這些傳統的電力系統解列措施仍然是繼電保護的思路，是一種被動解列.各裝置分散動作缺乏協調，且模型適應性差.而利用高速通信手段實時、全面、主動地監控系統狀態，動態地確定解列點和各解列點的動作時序，這種主動解列的方法是克服傳統方法缺陷的新思路［5］.一個系統的主動解列方案通常涉及到以下3個問題:

1)是否應該解列?即系統故障后的暫態穩定評估問題，對于這一傳統課題目前已擁有大量的研究［6-7］.

2)在哪里解列?即解列點的選取問題;通常解列點的選取至少應滿足2點:一是解列后的子系統中各發電機間應保持同步運行;二是解列后的子系統中發電機與負荷的功率應盡量保持平衡.文獻［8-12］對這一問題提出了較為成熟的思路.但以上方法都要基于故障后發電機分群信息已知的條件下進行.

3)什么時候解列?即解列時刻的選取應盡量保證對系統的沖擊達到最小，使子系統從振蕩中快速平息.通常認為能夠解列的最早時刻是振蕩半個周期時，即聯絡線兩側母線電壓相位差為180°.若考慮斷路器的開斷電流的大小，則通常在一個完整的振蕩周期結束時解列系統［13-14］.

本文在pmu量測信息的基礎上，從能量角度探討系統失步解列所涉及到的問題.

1 支路能量特點分析

系統中支路傳輸的有功功率表達式為

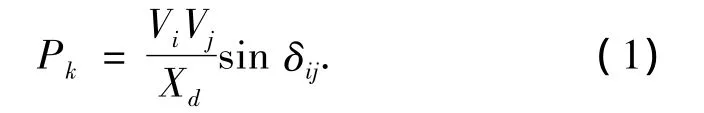
式中:Vi、Vj分別為支路兩側節點電壓幅值，Xd為支路電抗，δij為支路兩端電壓相角差.

則以故障清除時刻支路兩端電壓相角差δijc為參考點，故障后沿實際故障軌跡的支路能量定義為

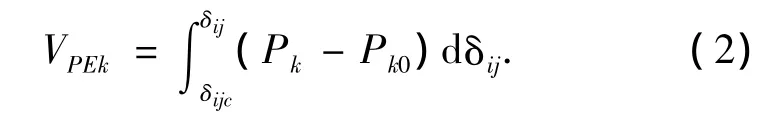
式中:Pk0為故障后穩定平衡點處的支路有功功率.

沿實際故障軌跡的全系統的暫態能量表達式為

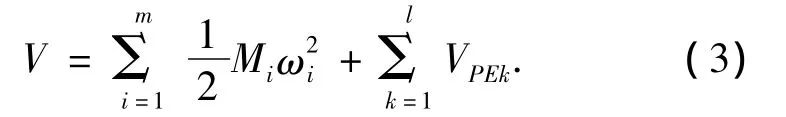
當忽略發電機的阻尼作用及線路電阻的熱耗散時，系統的暫態能量V沿系統故障后軌跡是守恒的［15］.也就是說沿故障后軌跡，系統所有發電機的動能與所有支路能量進行等量的交換.

當系統受到大干擾失步以后，隨著發電機轉速不斷增大，動能增加，隨時間增長趨于無窮大，不再有界.由能量守恒可知，系統的支路勢能會等量減小，并隨時間的增長趨于反向無窮大，仿真表明，并不是所有支路能量都呈現相同的變化趨勢，而只有部分支路能量趨于反向無窮大，其余支路能量都在一個有界范圍內變化.而當系統不失步時，所有支路勢能都在一個有界范圍內變化.

因此可通過故障后支路能量是否趨于無窮大的特征來判斷系統的穩定性，但以這一特征作為系統是否穩定判據不夠精準且計算所需時間較長，實際上故障發生后應在盡可能短的時間內判斷出系統的穩定性.文獻［15］通過理論分析及仿真，將這一特征轉化成為精確的量化指標來評估系統穩定性.即支路在第一擺振蕩過程中穩定度指標定義為

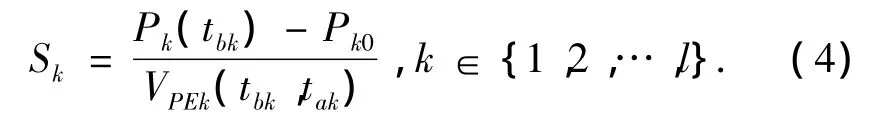
式中:ta、tb分別為故障后支路k的能量第1次達到最小值，最大值對應的時刻.當Sk=0時，支路“失穩”，即支路能量將隨時間推移趨于無窮大，系統失穩;Sk≠0時，支路“穩定”，即支路能量在一個有界范圍內變化.因此只要有一條支路Sk=0，則系統失穩;所有支路的Sk≠0，則系統穩定.通常在支路有功振蕩的半個周期之前即可判斷出系統的穩定性，為接下來的解列操作爭取了時間.

2 解列地點選取問題

2.1 失步中心斷面確定

當系統發生失步以后，失步斷面聯絡線(異步振蕩支路)有功周期性過零振蕩，支路兩側母線電壓的相位角差在0°～360°周期性變化［2］.由式(1)可知，失步斷面聯絡線有功功率周期性過零正是由于失步中心兩側的母線電壓的相位角差在0°～360°范圍內周期性變化所造成的.同步振蕩支路有功功率振蕩幅度較弱，但也會有部分支路過零振蕩，但此功率過零振蕩并非兩端電壓相角差過180°所致，而是兩端電壓相角差由正變負導致的.

如圖1所示分別為異步振蕩支路和同步振蕩支路故障后的兩端電壓相角差與支路能量關系曲線.從圖1(a)可以看出，當異步振蕩支路的支路能量第一次達最大值對應時刻tbk之后，兩端電壓相角差繼續增大，即

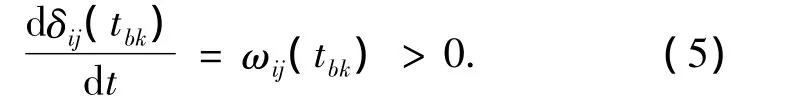
而在tbk時刻必有:

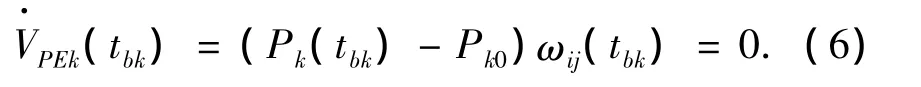
則

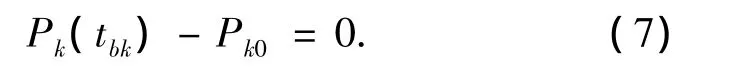
將式(7)代入式(4)可得Sk=0.

從圖1(b)可以看出，當同步振蕩支路的支路能量第1次達最大值對應時刻tbk之后，支路兩端電壓相角差開始減小，同樣道理可推得Sk≠0.

因此上一節中系統失步判據中所判得的失穩支路即為異步振蕩支路，所有的異步振蕩支路構成的斷面即為失步中心所在斷面.以上方法能夠準確判斷同步振蕩支路與異步振蕩支路，避免了運用有功功率過零等特征而發生誤判的可能.

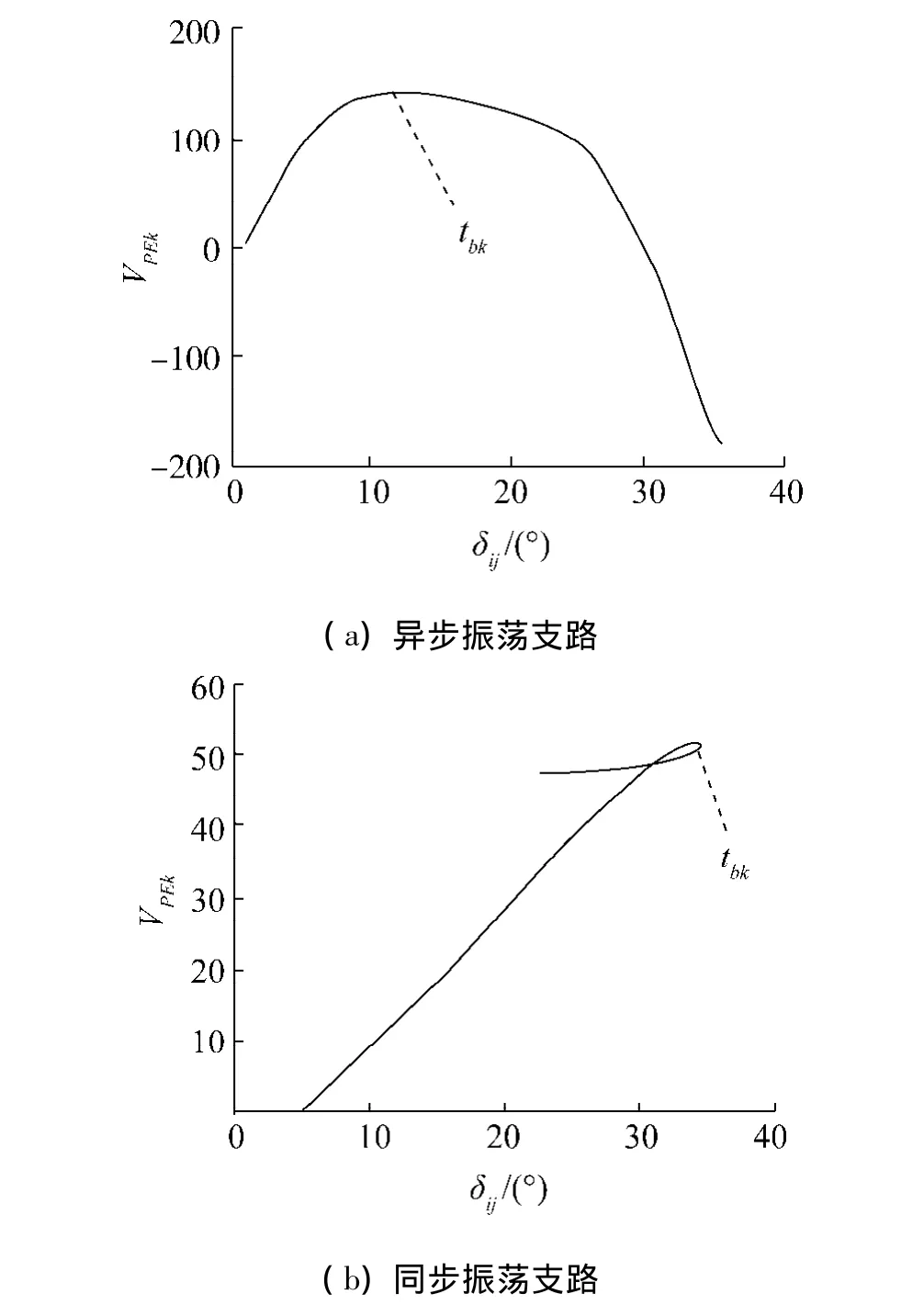
圖1 故障后支路兩端電壓相角差與支路能量關系曲線Fig.1 Curve of branch voltage angle difference and branch energy

2.2 解列面搜索

從支路角度來看，系統是否穩定取決于故障后發電機動能是否在一段時間內能夠被網絡完全吸收，即發電機動能是否能夠完全轉化為增廣網絡支路勢能.系統失穩成為角度不同步的2部分，是因為處于失步中心所在支路其傳輸有功功率方向呈周期性反復振蕩，近似于一個周期內傳輸有功功率為零，導致送電端缺失了一些供電的支路和負荷，也就缺失了一部分用來轉化發電機動能的支路勢能.因此，導致送電端發電機動能不能完全被吸收而最終成為臨界機群而失穩，以失步中心所屬斷面為分割線的兩側系統相互失去穩定.假設系統為2機群失穩模式，圖2為失穩的2機群系統及失步中心斷面示意.

圖2 失穩的兩機群系統及失步中心斷面示意Fig.2 Two unstable machines and out-of-step interface

由上面分析可知，解列后系統是否穩定取決于動能是否在一段時間內能夠完全轉化為支路勢能.對于系統A來說，應從系統B多劃分一些支路負荷給它來吸收系統中大量的動能才可能使系統穩定.

解列點的選取應滿足的基本條件按重要程度依次為(假設為兩機群失穩模式):

1)被解列的各子系統內部同步運行.2個子系統之間的任意斷面都可滿足這一條件;

2)解列后各子系統內部靜態功率基本平衡.若要保證嚴格的靜態功率平衡通常會導致系統無解，因此通常留有一定裕量，即解列后各子系統|Σ Pm－Σ Pe|＜ε即可，ε的大小取決于子系統的出力上下限值.

3)解列后各子系統應盡快過渡到穩定運行狀態.由于非臨界機通常偏離穩定點較小，其自身調節能力較強;而臨界機通常偏離穩定點較大，其自身調節能力較弱.因此這里重點關注的應是臨界機群所屬系統的穩定性問題.通常對于臨界機群所屬系統A有Σ Pm＞Σ Pe，導致機群加速，若解列后系統A的有Σ Pm＜Σ Pe，則能夠抑制機群的加速從而快速過渡到穩定狀態.同理使系統B有Σ Pm＞Σ Pe.也就是說在滿足條件2)中的裕量ε的同時，應使臨界機群系統稍微過負荷，非臨界機群系統稍微欠負荷.功率不平衡的部分可由系統調速裝置來調節，當然臨界機群系統的總負荷量不應超過可發電上限值.

4)解列時盡量不破壞系統的原始潮流路徑.則搜索時應沿著失步中心斷面所含支路的有功功率方向搜索負荷，直至搜索到的負荷量與支路功率相當.

因此從失步中心斷面出發，采用深度優先搜索加校驗的方法尋找解列面.假設以失步中心斷面功率流動方向為正，具體措施如下:通過式(4)即可判斷失穩時失步中心所屬斷面.從此斷面出發，沿支路有功功率流動方向進行深度搜索負荷，直至搜索到的負荷總量Σ Pl大于支路功率Pb為止(若遇到發電機節點時或搜索到的負荷節點與其他支路搜索到的為同一節點時，則立即停止搜索)，記ΔP=Σ Pl－Pb，并將對應的負荷節點納入另一系統中.用同樣方法依次搜索完失步中心斷面所有支路所對應的負荷節點后，檢測新的斷面有功功率Pc，若0＞Pc＞－ε，則結束搜索，在此斷面解列系統.若Pc＜－ε，則應將正方向支路(如圖2中支路1、2)的部分負荷還回原系統中，各個支路按照ΔP由大到小排序，依次去掉支路中搜索到的最后一個負荷，直至滿足結束條件0＞Pc＞－ε為止，從此處解列系統.若Pc＞0，則應將反方向支路(如圖2中支路n)的部分負荷還回原系統中，具體實施方法與正方向支路相同.解列面搜索流程如圖3所示.

圖3 解列面搜索流程Fig.3 Searching split interface flow chart

3 解列時刻確定

前面已提到，利用支路能量判斷系統失步中心可在半個振蕩周期之前完成，解列面搜索過程也不復雜，因此直到判斷出解列面都可在半個周期之前完成.如果在半個周期之前解列系統，對系統的暫態過程會造成怎樣的沖擊?對于失穩后的兩機群系統A、B，若將每一機群看做一臺等值機，則2臺等值機的轉子運動方程可表達［16］為

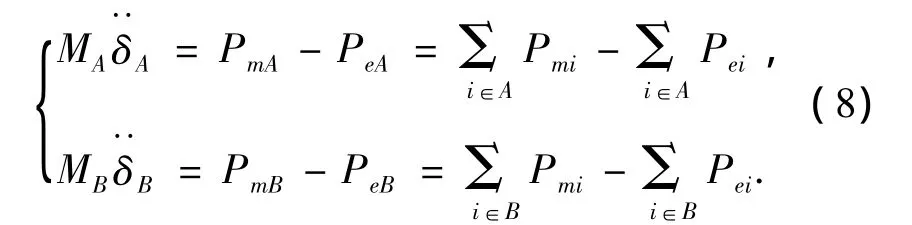
圖4為A、B等值機故障及解列過程中的電磁功率、機械功率結果.其中實線為解列面確定之后(電磁功率半個振蕩周期之前)解列的A、B等值機電磁功率PeA，PeB，對應的解列時刻為tx，點線為在半個振蕩周期解列時的A、B等值機電磁功率PeA，PeB，對應的解列時刻為ty，虛線為A、B等值機的機械功率PmA，PmB.

由式(8)可知，若PmA(PmB)＞PeA(PeB)，則機組積累動能加速，若PmA(PmB)＜PeA(PeB)，則機組動能轉化為勢能減速.從圖4可看出，無論是A等值機還是B等值機，在ty時刻解列都要比在tx時刻解列多積累陰影部分面積的動能，相應的速度也增加，因此在tx時刻解列系統更有利于系統最終恢復穩定狀態.

因此在判斷出解列斷面之后可立即解列系統，更有利于系統暫態穩定的恢復.

圖4 A、B等值機故障及解列過程中的電磁功率、機械功率曲線Fig.4 Curve of A，B equivalence machines＇electromagnetic power and mechanical power during fault and split

4 算例分析

以IEEE-68系統為例，對本文的方法進行分析驗證.IEEE-68系統是新英格蘭系統和紐約系統的互聯系統，互聯系統一般具有區域內部電氣連接緊密、區域間弱聯接的特性，是典型的適合解列的系統［17］.

假設支路55－18靠近節點55一側0s發生三相接地短路，持續0.3s清除故障.發電機采用Eq'恒定模型，考慮阻尼及部分調速器的作用，負荷為恒阻抗.并假定ε=1.

1)判斷系統穩定性并尋找失步中心斷面.

從故障后時刻開始計算各個支路的支路能量，當支路能量第一次達到最大值時(對應時刻tbk)，按照式(4)計算支路穩定度指標，計算求得:S54－53= S27－53=S60－61=0，其余支路穩定度指標均不為零.因此系統就以支路54－53，27－53，60－61組成的斷面a為分界線，呈現兩機群失穩模式，且根據斷面初始有功的流向可知，G1～G9為臨界機群，G10～G16為非臨界機群.且失步中心斷面就為斷面a，如圖5所示.

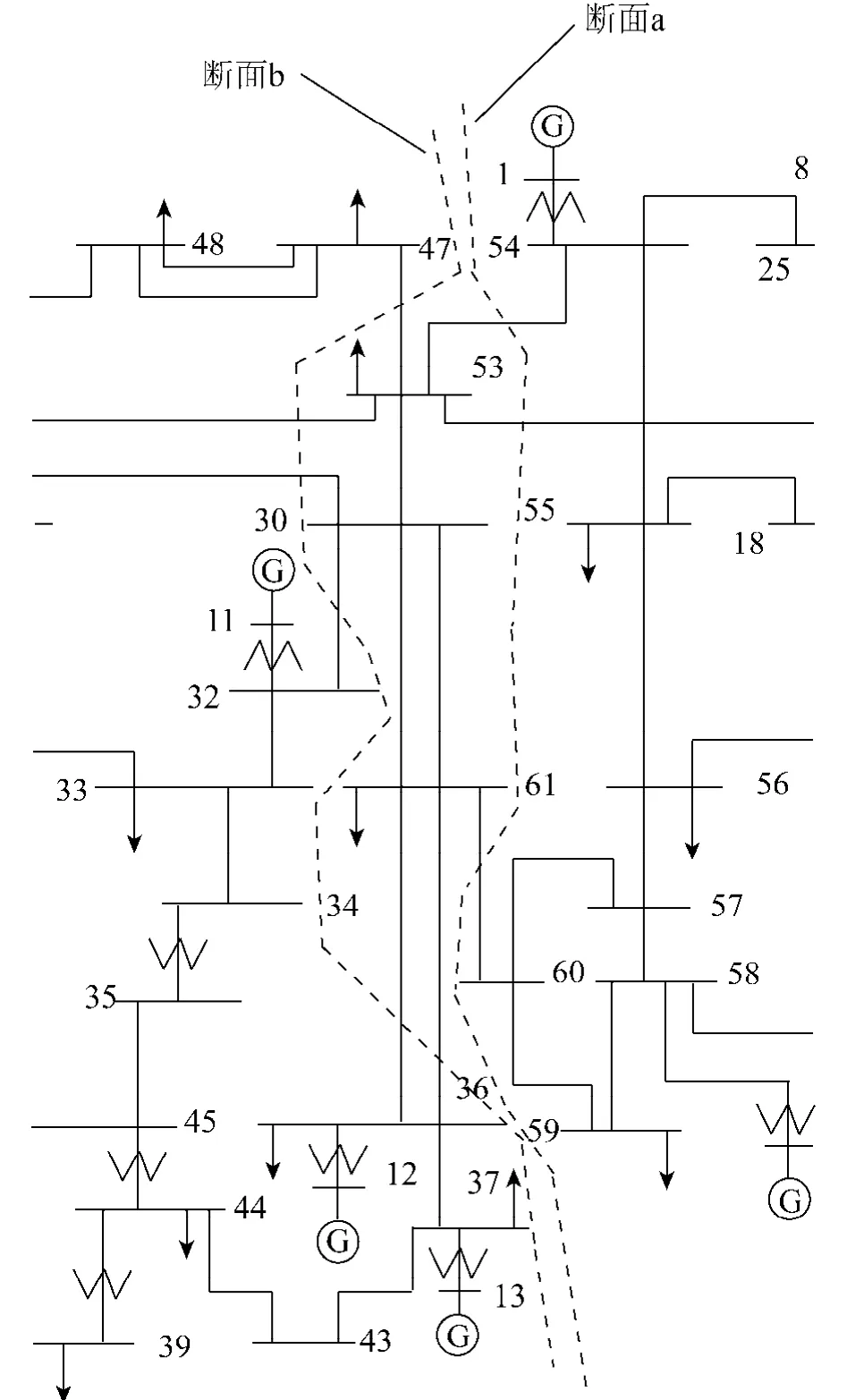
圖5 IEEE－68節點部分系統示意Fig.5 Part of IEEE－68 node system

2)搜索解列面.

從失步中心斷面出發沿各個支路初始有功方向搜索解列面.支路54－53初始有功為1.309 23(P.U.)，方向為由54節點流向53節點，因此搜索53節點負荷，負荷有功為2.527，已大于支路有功值，停止搜索;支路27－53初始有功為0.233 19，方向為由27節點流向53節點，因此搜索53節點負荷，與上一條支路搜索路徑相同，停止搜索;支路60－61初始有功為1.318 24，方向為由60節點流向61節點，因此搜索61節點負荷，負荷有功為1.04，小于支路有功，繼續沿61節點尋找相連節點12、30，節點12直接與發電機節點相連，所以終止搜索，節點30沒有負荷，繼續沿30節點尋找相連節點31、32，發現節點31、32都直接與發電機相連，因此終止搜索.搜索到的總負荷量為Pl53+Pl61=3.567，失步中心斷面功率為P54－53+P27－53+P60－61=2.860 66，若忽略網絡損耗，新斷面b有功:Pc1=2.860 66－3.567=－0.706 34，滿足0＞Pc1＞－ε，因此應在此斷面解列，即在由支路47－53，31－53，31－30，32－30，61－36(雙回線)組成的斷面b解列，如圖5所示.

判斷出解列面的時間為1.1 s，在此刻解列系統，解列后系統穩定情況如圖6所示.圖6為兩機群發電機角速度變化過程，從中可看出機群A的發電機大約在50 s時角速度就保持同步了，系統也就穩定運行了.機群B的發電機大約在100 s時穩定.

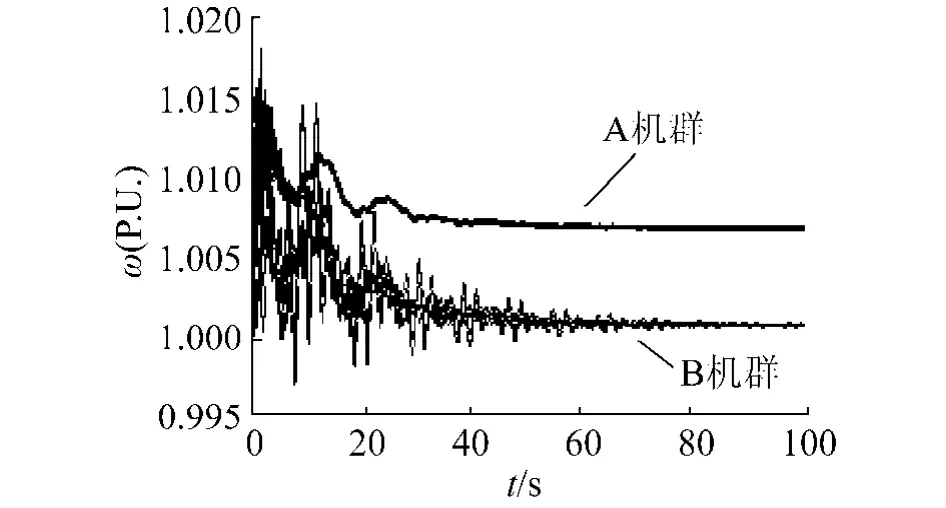
圖6 斷面b處解列時各發電機的角速度變化過程Fig.6 Each machine angle rate change when splitting interface b

若使兩系統的功率不平衡度最小，則應將61節點負荷歸還原系統，此時新斷面 c有功 Pc2= 2.860 66－2.527=0.333 66，此時0＜Pc2＜ε，新斷面c解列后系統穩定情況如圖7所示.

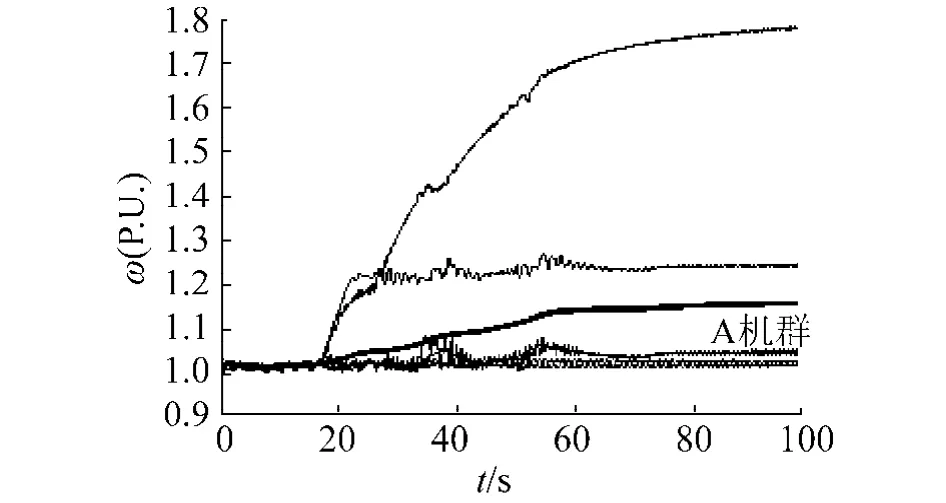
圖7 斷面c處解列時各發電機的角速度變化過程Fig.7 Each machine angle rate change when splitting interface c

圖7為B機群各發電機的角速度變化過程，由圖可見隨時間增加發電機角速度發散開來，系統不穩定.由此可見，解列時應使臨界集群稍稍過負荷比欠負荷更容易穩定.

5 結論

本文在pmu量測信息的基礎上，從能量角度探討系統失步解列所涉及到的問題.得出結論如下:

1)根據支路能量故障后的變化特點不但可以判斷系統的穩定性，并能夠確定系統失步中心斷面，為解列面的搜索提供了切入點.

2)從系統動能與勢能相互轉換關系入手，以失步中心斷面為起點，根據功率平衡約束所確定的系統解列面能使解列后子系統更易于恢復穩定，且無需故障后發電機的分群信息及網絡化簡、等值.

3)從解列后子系統積聚動能大小的角度分析了系統的解列時刻，認為解列時刻應采取盡可能快的原則才更有利于故障后子系統暫態穩定的恢復.

［1］袁季修.試論防止電力系統大面積停電的緊急控制-電力系統安全穩定運行的第三道防線［J］.電網技術，1999，23(4):1-4.

YUAN Jixiu.Emergency control for preventing widespread blackout of power system the third line of defence［J］.Power System Technology，1999，23(4):1-4.

［2］張保會.加強繼電保護與緊急控制系統的研究提高互聯電網安全防御能力［J］.中國電機工程學報，2004，24 (7):1-6.

ZHANG Baohui.Strengthen the protection relay and urgency control systems to improve the capability of security in the interconnected power network［J］.Proceedings of the Csee，2004，24(7):1-6.

［3］張保會，張毅剛，劉海濤.基于本地量的振蕩解列裝置原理研究［J］.中國電機工程學報，2001，21(12):67-72

ZHANG Baohui，ZHANG Yigang，LIU Haitao.Study on principle of power system separation device based on local electrical parameter［J］.Proceedings of the Csee，2001，21 (12):67-72.

［4］潘貞存，桑在中，戴方濤，等.電網自動解列的新判據［J］.電力系統自動化，1995，19(7):34-37.

PAN Zhencun，SANG Zaizhong，DAI Fangtao，et al.A new criterion for power system automatic separation［J］.Automation of Electric Power Systems，1995，19(7):34-37.

［5］沈沉，吳佳耘，喬穎，等.電力系統主動解列控制方法的研究［J］.中國電機工程學報，2006，26(13):1-6.

SHEN Chen，WU Jiayun，QIAO Ying，et al.Studies on active splitting control of power systems［J］.Proceedings of the Csee，2006，26(13):1-6.

［6］XUE Y.Integrated extended equal area criterion-theory and applications［J］.Electricity(English Journal of CSEE)，1995(4):97-103.

［7］STANTON S E，SLIVINSKY C，MARTIN K，et al.Application of phasor measurements and partial energy analysis in stability large disturbances［J］.IEEE Trans on PWRS，1995，10(1):297-306.

［8］SUN K，ZHENG D，LU Q.Splitting strategies for islanding operation of large-scale power systems using OBDD-based methods［J］.IEEE Transactions on Power Systems，2003，18(2):912-922.

［9］ZHAO Q，SUN K，ZHENG D，et al.A study of system splitting strategies for island operation of power system:a two-phase method based on OBDD［J］.IEEE Transactions on Power Systems，2003，18(4):1556-1665.

［10］SUN K，ZHENG D，LU Q.A simulation study of OBDD-based proper splitting strategies for power systems underconsideration of transient stability［J］.IEEE Transactions on Power Systems，2005，20(1):389-399.

［11］汪成根，張保會，李鵬，等.基于自適應解列的電力系統解列面快速搜索［J］.西安交通大學學報，2009，43(2): 90-95.

WANG Chenggen，ZHANG Baohui，LI Peng，et al.Fast search for islanding strategy based on self-adaptive system islanding［J］.Journal of Xi＇an Jiaotong University，2009，43(2):90-95.

［12］段振國，高曙，楊以涵，等.基于圖論理論的電力系統解列策略生成方法［J］.中國電力，1998，31(3):7-9.

DUAN Zhenguo，GAO Shu，YANG Yihan，et al.A method of determining the point of system splitting based on graph theory［J］.China Power，1998，31(3):7-9.

［13］陳西穎，李衛星，郭志忠.電力系統失步解列研究［J］.繼電器，2006，34(8):30-34.

CHEN Xiying，LI Weixing，GUO Zhizhong.Research of wide area measure system based criteria for detecting the synchronization loss for power system［J］.Relay，2006，34 (8):30-34.

［14］HOU D，TZIOUVARAS D A.Out-of-step pretection enhancements［C］//The Eighth IEE International Conference on Developments in Power System Protection.Amsterdam，Netherlands，2004:135-139.

［15］蔡國偉，穆鋼，CHAN K W，等.基于網絡信息的暫態穩定性定量分析-支路勢能法［J］.中國電機工程學報，2004，24(5):1-6.

CAI Guowei;MU Gang，CHAN K W，et al.Branch potential energy method for power system transient stability assessment based on network dynamic variables［J］.Proceedings of the Csee，2004，24(5):1-6.

［16］倪以信，陳壽孫.動態電力系統的理論和分析［M］.北京:清華大學出版社，2002:350.

NI Yixin，CHEN Shousun.Dynamic power system analysis［M］.Beijing:Tsinghua University Press，2002:350.

［17］喬穎，沈沉，盧強.大規模電網解列控制可行性判斷［J］.中國電機工程學報，2008，28(25):50-55.

QIAI Ying，SHEN Chen，LU Qiang.Study on feasibility of islanding control of large-scale power systems［J］.Proceedings of the Csee，2008，28(25):50-55.